环形光场二维场强分布

环形光场在极坐标系下径向分布表达式：
MATLAB代码如下：

clc
clear all
close all
N = 200;           %取样点数200
lambda = 632e-9;   %波长632nm
k = 2*pi/lambda;   %波数

%环形光场径向分布参数设置
I0 = 3e9;          %初始光强
r0 = 4;            %光束半径
                   %超高斯光束阶数M,设置成m
w0 = 2;            %光腰半宽

%坐标系设置
x = linspace(-10,10,N);     %产生-10到200步长为10的数组
y = linspace(-10,10,N);
[X,Y] = meshgrid(x,y);      %生成X,Y矩阵
[theta,r] = cart2pol(X,Y);  %将笛卡尔坐标系转化为极坐标系

%生成图像
figure;
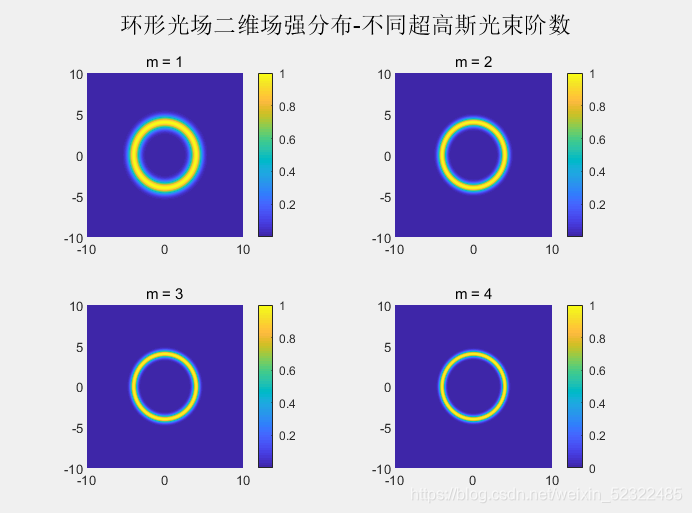
for m = 1 : 4                     %超高斯光束阶数，从1到4
    subplot(2,2,m)                %画布上生成2×2个子图，从第m个图开始画
    E1 = sqrt(I0).*(exp(-(r-r0).^2*m)./(w0^2*m)+exp(-(r+r0).^2*m)./(w0^2*m));  %极坐标下径向分布光强表达式
    I1 = E1.*conj(E1);            %光强等于电场强度乘以它的复共轭
    I1 = I1/max(max(I1));         %没看懂sos
    h1 = pcolor(x,y,I1);          %画彩色图
    colorbar;                     %生成色轴
    set(h1,'edgecolor','none','facecolor','interp');
    title(['m = ',num2str(m)]);   %显示标题
    %colormap(gray);               %输出灰度图像
end
suptitle('环形光场二维场强分布-不同超高斯光束阶数')   %为图片添加总标题

仿真结果：

参考文献：
[1]丁世鹏. 激光捕获技术及环形光束的聚焦特性研究[D].四川大学,2007.