2022年10月16日-19日，亚洲计算流体力学会议在韩国九州举办。会议涌现了不少结合人工智能技术进行流体力学模拟的论文成果，这说明人工智能技术逐渐渗透流体力学模拟领域。百度与西安交通大学的研究人员一起，利用飞桨框架和科学计算工具组件PaddleScience，首次实现了基于物理信息约束神经元网络（PINN）方法，利用极少量监督点模拟二维非定常不可压缩圆柱绕流，将同等条件的CFD流场求解耗时降低了3个数量级。因为会议论文在网上无法下载，因此附上该论文的详细介绍（图1为论文封面），方便感兴趣的研究人员了解论文情况以及飞桨和PaddleScience的能力。

• 会议论文代码下载地址

https://github.com/tianshao1992/PINNs_Cylinder

图1 ACFD2022会议收录摘要

研究背景

计算流体力学（Computational Fluid Dynamics, CFD）是研究流体力学问题的一种有效方法。CFD模拟通过在表示流体区域的网格上求解流体力学纳维-斯托克斯方程组（一种偏微分方程）来实现。在过去的几十年中，CFD模拟在模拟不同工程领域的流体问题方面取得了巨大进展，并已成为流体力学中的重要工具。

然而，CFD模拟存在一定的限制。当流体域和流场复杂时，网格生成可能是一项困难的任务。更细的网格可以给出更准确的结果，但它在时间和资源上的计算成本很高。通常，学者们会通过局部网格加密在精度和计算成本之间进行权

横

1

横^1

横1,。然而，这会导致另一个问题，即如果在相邻的局部网格块的交界处，网格尺寸变化太快，则交界处网格的质量可能会变差，因此即使进行了局部网格加密，也需要兼顾不同网格块之间的网格尺寸过渡。此外，不同物理现象需要不同的网格尺寸。例如，在CFD-DEM模拟中，需要对网格进行特殊的处理来适合细小颗粒的模

拟

2

拟^2

拟2。因此，如果CFD模拟不需要网格，则能从本质上克服上述挑战。物理信息约束的神经元网络（PINN

）

3

）^3

）3的出现，给无网格CFD模拟提供了一种可行方案。

本论文利用飞桨框架和科学计算工具组件PaddleScience，首次实现了基于物理信息约束神经元网络（PINN）方法，利用极少量监督点模拟二维非定常不可压缩圆柱绕流。通过与基于有限体积法（FVM）的CFD求解方法对比，证明PINN方法在求解精度上能够达到FVM方法同等的精度。同时利用预先训练好的网络模型，每个时间步的结果预测只需8ms，远远快于FVM方法计算速度，这是因为PINN方法可以在GPU上实现不同时间步的并行计算。但是PINN模型的训练较为耗时，未来需要开发更高效的算法来解决训练耗时长的问题。

研究方法

二维非定常不可压圆柱绕流问题描述

二维非定常不可压缩圆柱绕流是一种典型的非定常不可压缩流体现象，包含了流动边界层、流动分离、逆压梯度、粘性耗散等典型的流动现象，常常被用来验证数值求解算法。在本论文中，我们也选用圆柱绕流作为验证案例，选取的圆柱绕流几何和边界设置如图2所示。

整体流动为长方形区域，左侧为速度入口，右侧为压力出口，上下界面为无限远界面（即不设置边界条件），中间放置了一个直径为D=1cm的圆柱。圆柱表面满足无滑移条件，速度为0m/s。左侧入口的速度为1m/s，右侧的压力为0Pa。流体的运动粘性系数为0.4c

m

2

m^2

m2/s，密度为1kg/

m

3

m^3

m3。根据上述参数，可以确定流动的雷诺数Re=250。流动的初始时刻状态由CFD软件OpenFOAM进行非定常模拟结果得到，其中OpenFOAM的时间步长设置为0.5ms。这里说明下，OpenFOAM采用的是有限体积方法（FVM）去求解下列纳维-斯托克斯方程组：

∇

⋅

u

=

0

\mathrm{\nabla}·u=0

∇⋅u=0 (1)

∂

u

∂

t

+

u

∙

∇

u

+

1

ρ

∇

p

−

ν

∇

2

u

−

f

=

0

\frac{\partial\mathrm{u}}{\partial t}+\mathrm{u}∙∇u+\frac{1}{\rho}\mathrm{\nabla}\mathrm{p}-ν\mathrm{\nabla}^2u-f = 0

∂t∂u​+u∙∇u+ρ1​∇p−ν∇2u−f=0 (2)

其中方程（1）为连续性方程，

u

\mathrm{u}

u代表速度矢量，

∇

⋅

u

\mathrm{\nabla}·u

∇⋅u表示进出控制体的质量差，因为本案例采用不可压缩流动，因此进出控制体的质量差为0；方程（2）为动量方程，

ν

\nu

ν表示流体运动粘性系数，

ρ

\rho

ρ表示流体密度，

p

p

p表示控制体上的静压，

f

\mathrm{f}

f表示作用在控制体上的体积力（本案例里为0）。

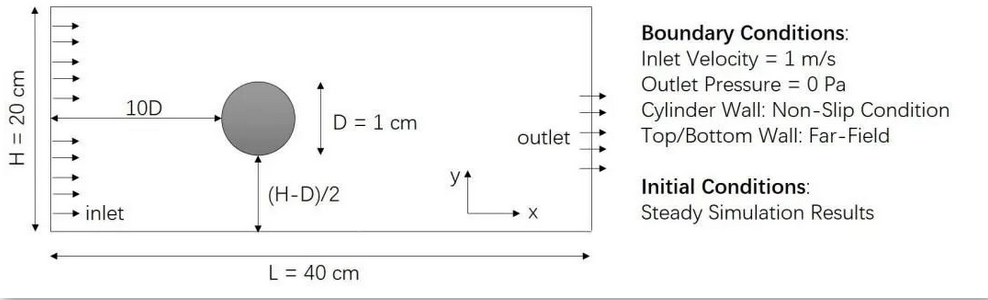
图2 二维圆柱绕流示意图及初始和边界条件

物理信息约束神经元网络（PINN）

区别于OpenFOAM的有限体积法（FVM），物理信息约束神经元网络（PINN）利用神经元网络能逼近任意光滑函数的能力，来进行无网格求解纳维-斯托克斯方程组。本文构建的PINN网络结构示意图如图3所示。

神经元网络为一个全连接层网络，输入为3个神经元节点，分别对应流动的时间（t）和坐标（x，y），输出为3个神经元节点，分别对应流动的横向速度（u）、纵向速度（v）和静压（p）。在图3中，为了简便表达，采用速度矢量形式（u）来展示。

为了求解纳维-斯托克斯方程组，在神经元网络的损失函数项引入了物理信息约束，使得神经元网络既可以在数据层面得到训练，也可以在物理规律层面得到训练。具体损失函数的定义方式见下一节。

本文采用的神经元网络参数见表1。除了输入和输出的神经元节点，一共有6层隐藏层，每层包含64个神经元节点，激活函数为tanh，优化器为Adam，初始学习率为0.001，训练迭代步数为40万。

表1 神经元网络参数设置

图3 物理信息约束神经元网络结构示意

PINN的损失函数

神经元网络的训练过程，是通过损失函数的反向传递来实现网络参数的更新。本文中，损失函数包含数据项和物理规律项：

J

=

J

d

+

ω

J

p

J=J_d+\omega J_p

J=Jd​+ωJp​(3)

其中,

J

J

J是神经元网络的总损失函数，

J

d

J_d

Jd​是数据项损失函数，

J

p

J_p

Jp​是物理规律项损失函数，

ω

\omega

ω是物理规律项的权重。

当

ω

=

0

\omega=0

ω=0时，该神经元网络就是普通的神经元网络。通过设置

ω

≠

0

\omega\neq0

ω=0，在损失函数中引入物理规律的影响，增强神经元网络对物理规律的拟合能力。物理规律损失函数项通过神经元网络自身的微分传递链计算得到。

数据项损失函数（

J

d

J_d

Jd​）定义为预测数值与真实数值之间的均方差（MSE）:

J

d

=

1

N

d

∑

i

=

1

N

d

∣

Y

p

r

e

d

i

−

Y

t

r

u

e

i

∣

2

J_d=\frac{1}{N_d}\sum_{i=1}^{N_d}\left|Y_{pred}^i-Y_{true}^i\right|^2

Jd​=Nd​1​∑i=1Nd​​
​Ypredi​−Ytruei​
​2(4)

其中，

N

d

N_d

Nd​代表用来构造数据项损失的监督点数目，Y表示用来比较的物理量，真实数值为OpenFOAM计算结果；监督点指已知流场物理量数值的点，值得注意的是，监督点数目可以比OpenFOAM里的网格点数少。物理项损失函数（

J

p

J_p

Jp​）定义为：

J

p

=

J

P

D

E

+

J

B

C

+

J

I

C

J_p=J_{PDE}+J_{BC}+J_{IC}

Jp​=JPDE​+JBC​+JIC​(5)

其中，

J

P

D

E

J_{PDE}

JPDE​代表了流体偏微分方程的损失函数项，这也是PINN网络必不可少的一项；

J

B

C

J_{BC}

JBC​代表了流体系统的边界条件损失函数项，代表了流体系统的初始条件损失函数项。

J

P

D

E

J_{PDE}

JPDE​，

J

B

C

J_{BC}

JBC​和

J

I

C

J_{IC}

JIC​的定义如下:

J

P

D

E

=

1

N

f

∑

i

=

1

N

f

∣

G

(

u

i

,

p

i

)

∣

2

J_{PDE}=\frac{1}{N_f}\sum_{i=1}^{N_f}\left|G\left({u}^i,p^i\right)\right|^2

JPDE​=Nf​1​∑i=1Nf​​
​G(ui,pi)
​2 (6)

J

B

C

=

1

N

B

C

∑

i

=

1

N

B

C

∣

Y

p

r

e

d

i

−

Y

t

r

u

e

i

∣

2

J_{BC}=\frac{1}{N_{BC}}\sum_{i=1}^{N_{BC}}\left|Y_{pred}^i-Y_{true}^i\right|^2

JBC​=NBC​1​∑i=1NBC​​
​Ypredi​−Ytruei​
​2 (7)

J

I

C

=

1

N

I

C

∑

i

=

1

N

I

C

∣

Y

p

r

e

d

i

−

Y

t

r

u

e

i

∣

2

J_{IC}=\frac{1}{N_{IC}}\sum_{i=1}^{N_{IC}}\left|Y_{pred}^i-Y_{true}^i\right|^2

JIC​=NIC​1​∑i=1NIC​​
​Ypredi​−Ytruei​
​2 (8)

其中，

N

f

N_f

Nf​是用于计算流体偏微分方程损失函数的数据点数量，

N

B

C

N_{BC}

NBC​是用于计算流体系统边界条件损失函数的数据点数量，

N

I

C

N_{IC}

NIC​是用于计算流体系统初始条件损失函数的数据点数量，

G

G

G代表了流体系统的即纳维-斯托克斯方程组的隐式格式，理想的情况下

G

=

0

G=0

G=0。

流体系统的总损失函数定义为：

J

=

ω

1

J

d

+

ω

2

J

P

D

E

+

ω

3

J

B

C

+

ω

4

J

I

C

J=\omega_1J_d+\omega_2J_{PDE}+\omega_3J_{BC}+\omega_4J_{IC}

J=ω1​Jd​+ω2​JPDE​+ω3​JBC​+ω4​JIC​ (9)

其中

ω

1

,

 

ω

2

,

 

ω

3

,

 

ω

4

\omega_1,\ \omega_2,\ \omega_3,\ \omega_4

ω1​, ω2​, ω3​, ω4​是各损失函数项的权重。区别于方程（3），方程（9）提供了一个更方便调节各损失函数项权重的定义。本文中

ω

1

=

ω

3

=

ω

4

=

10

,

 

 

ω

2

=

1

\omega_1=\omega_3=\omega_4=10,\ {\ \omega}_2=1

ω1​=ω3​=ω4​=10,  ω2​=1。

PINN的监督点分布

结合之前我们已经实现的基于大量监督点的PINN方法准确求解二维度非定常圆柱绕

流

4

流^4

流4，本文我们进一步探索了监督点数量对PINN求解的影响，因为监督点的数目既影响模型的计算速度，也影响模型对数据的依赖性。减少监督点数量，既可以提高模型计算速度，也可以降低模型对数据的依赖性。为此，我们设计了6种不同的监督点分布，监督点数量从4到68，如图4所示。

N

d

=

68

N_d=68

Nd​=68的监督点分布存在两种方式，a方案在圆柱前缘也布置一些点，b方案则所有点均在圆柱后方。

N

d

=

34

N_d=34

Nd​=34的监督点分布存在两种方式，a方案集中在圆柱近后方，b方案则分散在圆柱近和远后方。

N

d

=

16

N_d=16

Nd​=16和

N

d

=

4

N_d=4

Nd​=4的监督点分布的区别在于

N

d

=

4

N_d=4

Nd​=4仅在圆柱表面均分分布4个监督点。

图4 圆柱周围监督点布局

研究结果

PINN的训练过程

根据表1给的参数，在NVIDIA V100-32GB显卡上进行了不同监督点布局的模型训练。在训练40万步后，各损失函数项均收敛，其中一个模型的训练损失函数下降曲线如图5所示。

图5 PINN训练过程损失函数曲线

PINN与FVM对比

利用训练好的模型，我们将PINN计算的结果与OpenFOAM的FVM方法计算结果对比，如图6和图7所示。可以看到，在所有的监督点布局情况下，对全流场信息（u, v, p）PINN均能取得与OpenFOAM的FVM方法接近的计算结果，两者的绝对误差从全流场来看也较低。对于

N

d

=

4

N_d=4

Nd​=4的监督点布局，PINN的计算结果也能较好的捕捉到圆柱后涡的脱落现象。

进一步的，圆柱表面的升力和阻力也进行了对比，见图8。从对比结果来看，PINN可以在只需要4个监督点的情况下，得到与OpenFOAM类似的结果。

表2对比了训练好的PINN与OpenFOAM的FVM方法的计算耗时，可见在类似计算配置的情况下，PINN方法比OpenFOAM的FVM减少了3个数量级的计算耗时。

表2 PINN与FVM计算耗时对比

图6 不同监督点布局下PINN与FVM方法对比（静压、横向流速、纵向流速）

图7 不同监督点布局下PINN与FVM方法对比误差（静压、横向流速、纵向流速）

图8 不同监督点布局下PINN与FVM方法对比（升力和阻力）

结果讨论

通过二维非定常不可压缩圆柱绕流这个典型案例的论证，本文的结论表明PINN方法可以应用在求解非定常不可压缩流体力学，可以取得接近CFD方法类似的精度，同时在计算耗时上可以提升3个数量级。

但是PINN方法也有一定的局限性，一个关键的限制是目前采用的PINN方法依赖于CFD模拟产生的监督数据。尽管本论文的研究表明，只多4个监督点数据就可以满足PINN求解的需求，但是为了生成这4个监督点的数据，需要进行全流场的CFD模拟，而CFD模拟仍然面临网格质量、求解速度等问题。未来需要开发完全不依赖监督点的PINN方法，才能克服依赖CFD模拟数据的限制。

参考文献

[1] Teigland, R., & Eliassen, I. K. (2001). A multiblock/multilevel mesh refinement procedure for CFD computations. International journal for numerical methods in fluids, 36(5), 519-538.
[2] Volk, A., Ghia, U., & Stoltz, C. (2017). Effect of grid type and refinement method on CFD-DEM solution trend with grid size. Powder Technology, 311, 137-146.
[3] Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2017). Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv preprint arXiv:1711.10561.
[4] https://aistudio.baidu.com/aistudio/projectdetail/4178470

拓展阅读

1.【PaddlePaddle Hackathon 第四期】—飞桨科学计算 PaddleScience：
https://github.com/PaddlePaddle/Paddle/issues/50629#science

2. 飞桨AI for Science流体力学公开课第一期：
https://aistudio.baidu.com/aistudio/course/introduce/27926

3. AI+Science系列（三）：赛桨PaddleScience底层核心框架技术创新详解

4. 飞桨科学计算实训示例：
https://aistudio.baidu.com/aistudio/projectoverview/public?topic=15

相关地址

1. 飞桨AI for Science共创计划：

https://www.paddlepaddle.org.cn/science

2. 飞桨PPISG-Science小组：

https://www.paddlepaddle.org.cn/specialgroupdetail?id=9

3. 飞桨PaddleScience工具组件：

https://github.com/PaddlePaddle/PaddleScience