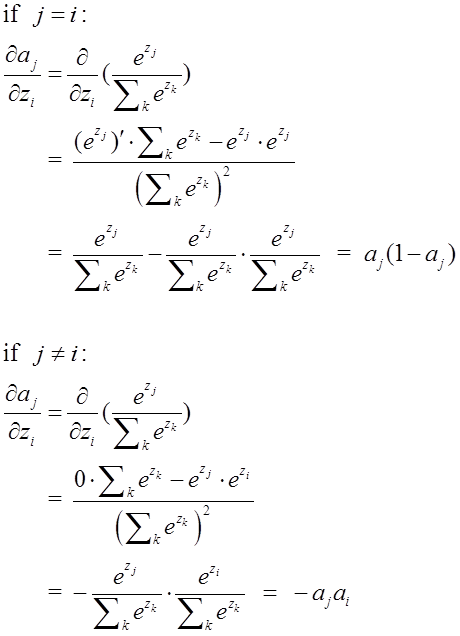Clarification：

1. 导数：一个函数在x处的变化量，即：导数本身是一个标量，x向左或者向右的变化率。
   1. 导数的方向可以任意指定
2. 偏微分：一个函数对其自变量变化率的描述，函数有多少个自变量就有多少偏微分
3. 梯度：把所有的偏微分当作向量来理解，梯度有方向和大小
   1. 梯度的长度反映：函数的变化趋势，即当前点的增长速率
   2. 梯度的方向：在当前点的增长方向

 一、How to search for minima?

1、Convex function

凸函数：在曲面上任意取两点：两点连线的中点的Z值（z1），大于曲面上该点对应的值(z2)，即 z1 > z2，因此该曲面代表的函数是凸函数。 

 2、Local Minima

 （1）实际例子——ResNet-56层

深度残差网络（Deep residual network, ResNet）的提出是CNN图像史上的一件里程碑事件。ResNet的作者何凯明也因此摘得CVPR2016最佳论文奖。

• ResNet就有很多的局部极小值，很容易陷在局部最小值里面
• 其实ResNet是解决了深度CNN模型难训练的问题
• ResNet通过残差学习解决了深度网络的退化问题，让我们可以训练出更深的网络，这称得上是深度网络的一个历史大突破吧。

 3、Saddle point（鞍点）

鞍点是一个比局部最小值更可怕的点，在求解过程中很有可能卡到这个点影响最小值点的求解。

 4、其他影响求解的地方

上面的局部最优解 和 鞍点都会影响最小值，还有一些因素也会对求解有影响：

• Initialization status（初始状态）：初始状态不同会影响求解的最小值的大小（可能会出现求解的是局部最小值而不是全局最小值）
  • 
• learning rate：开始如果不收敛学习率先设置小一点让它慢慢收敛（比如：0.1，0.01， 0.001），后期慢慢收敛后可以适当调整大一些
• momentum（动量） 

二、常见函数的梯度

 三、激活函数

h(x)函数会将输入信号的总和转换为输出信号，这种函数一般叫做激活函数。激活函数的作用在于决定如何来激活输入信号的总和。

• 激活函数是连接感知机和神经网络的桥梁
• 一般而言，朴素感知机是指单层网络，指的是激活函数使用的是阶跃函数的模型；多层感知机指的是神经网络，即使用了sigmoid等平滑的激活函数的多层网络。

0、阶跃函数（感知机时代）

 上述激活函数以阈值(threshold)为界，一旦超过阈值，就切换输出，这样的函数叫做：阶跃函数。其实激活函数从阶跃函数换成其他函数（平滑）就可以说是进入了神经网络时代

import torch
import numpy as np
from matplotlib import pyplot as plt

#阶跃函数,这种实现简单，但是不支持参数传递numpy数组
def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

#参数可传递numpy数组方式的实现
def step_plus(x):
    #判断操作，输出的y是一个布尔类型数组
    y = x>0 #x>0判断矩阵中的值是否都大于0
    #阶跃函数需要输出int类型，现在将其调整为输出int
    return y.astype(np.int)

def draw_step_pic():
    x = np.arange(-5.0, 5.0, 0.1)
    y = step_plus(x)
    #绘图
    plt.plot(x, y)
    plt.ylim(-0.1, 1.1) #指定y的范围
    plt.show()

if __name__ == '__main__':
    draw_step_pic()

1、激活机制

 2、sigmoid (Logistic)

 求导过程：

函数实现：

import torch
import numpy as np
from matplotlib import pyplot as plt

#sigmoid实现
#sigmoid函数能支持参数传递numpy数组是因为Numpy的广播功能
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

#绘制sigmoid函数的图形
def draw_sigmoid():
    x = np.arange(-5.0, 5.0, 0.1)
    y = sigmoid(x)
    plt.plot(x, y)
    plt.ylim(-0.1, 1.1) #指定y轴的范围
    plt.show()

if __name__ == '__main__':
    draw_sigmoid()

 torch.sigmoid

import torch
import numpy as np

def detect_gpu():
    print(torch.__version__)
    print(torch.cuda.is_available())

#sigmoid函数
def test():
    detect_gpu()
    #从-100到100分成10份
    a = torch.linspace(-100, 100 , 10)
    print(a)

    print(torch.sigmoid(a))

if __name__ == '__main__':
    test()

3、Tanh

Tanh激活函数常用于RNN

 torch.tanh

import torch
import numpy as np

def detect_gpu():
    print(torch.__version__)
    print(torch.cuda.is_available())

#sigmoid函数
def test():
    detect_gpu()
    a = torch.linspace(-1, 1, 10)
    print(a)
    print(torch.tanh(a))

if __name__ == '__main__':
    test()

 4、ReLU（Rectified Linear Unit）

ReLU函数可以说是目前深度学习的奠基石，主要原因在于：深度网络在向后传播的时候。ReLU函数的导数很稳定为1，不会放大也不会缩小，不会出现梯度离散或者爆炸情况

ReLU函数实现

import torch
import numpy as np
from matplotlib import pyplot as plt

#ReLU函数实现
#ReLU函数输出的特点：输入大于0直接输出该值，小于0
def relu(x):
    #np.maximum(0, x)函数会从输入的数值中选择比较大的数值进行输出
    return np.maximum(0, x)

#绘制图形
def draw_relu():
    x = np.arange(-5.0, 5.0, 0.1)
    y = relu(x)
    plt.plot(x, y)
    plt.show()

if __name__ == '__main__':
    draw_relu()

 案例

import torch
from  torch.nn import functional as F

#sigmoid函数
def test():
    a = torch.linspace(-1, 1, 10)
    print(a)
    #torch.relu
    print(torch.relu(a))
    #F.relu方式
    print(F.relu(a))

if __name__ == '__main__':
    test()

 四、LOSS及其梯度

 1、MSE

 

 2、Gradient API

（1）autograd.grad求导

autograd.grad是torch的自动求导的函数

import torch
from  torch.nn import functional as F

#autograd.grad自动求导
#pred = x*w + b
def test():
    x = torch.ones(1)
    print(x)
    w = torch.full([1], 2.)
    print(w)

    #设置参数需要梯度信息
    w.requires_grad_()
    #构建图，PyTorch是基于计算图来完成求导的
    mse = F.mse_loss(torch.ones(1), x*w)
    print("mse: {0}".format(mse))
    print(torch.autograd.grad(mse, [w]))

if __name__ == '__main__':
    test()

 （2）loss.backward

import torch
from  torch.nn import functional as F

#autograd.grad自动求导
#pred = x*w + b
def test():
    x = torch.ones(1)
    print(x)
    w = torch.full([1], 2.)
    print(w)

    #设置参数需要梯度信息
    w.requires_grad_()
    mse = F.mse_loss(torch.ones(1), x*w)
    print("mse: {0}".format(mse))
    print(mse.backward())
    print(w.grad)

if __name__ == '__main__':
    test()

 3、Softmax

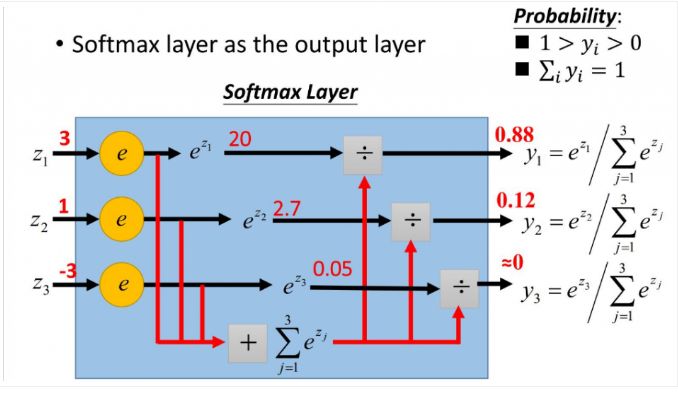
softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！这里描述用于分类的 Cross Entropy算法，该算法一般结合 Softmax一起使用

• softmax满足每一个值的取值区间在0~1，所有的概率加起来和是1
• softmax会把原来大的放的更大，原来小的压缩在一个比较密集的空间

softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！ 

参考博客：softmax函数以及相关求导

import torch
from  torch.nn import functional as F

def test():
    a = torch.rand(3)
    print(a)
    #参数设置梯度信息
    a.requires_grad_()
    p = F.softmax(a, dim=0)
    print(torch.autograd.grad(p[1], [a], retain_graph=True))
    print(torch.autograd.grad(p[2], [a]))

if __name__ == '__main__':
    test()