由退化函数H退化的图像复原的最简单的方法是直接作逆滤波，设图像退化前的傅里叶变换为F(u,v)，退化后的傅里叶变换为G(u,v)，系统函数即退化函数的傅里叶变换为H(u,v)。函数

所谓直接逆滤波，就是用退化函数除退化图像的傅里叶变换，获得退化前图像的傅里叶变换的估计，ui

d4b862c6c539aa37416e911aa36565da.png为F(u,v)的估计，则

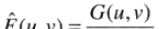72a77f735f7ff719fa5de39834f4a664.png，同时

689af337deee17f69e064893c57208a0.png，其中N(u,v)为噪声的傅里叶变换。所以，可得

9c409fa3303c5c9db110a098aede0c0a.png，由该式可知，即便知道退化函数，也不能准确的复原图像，由于N(u,v)未知，甚至有更糟的状况是若是退化函数是零或是很是小的值，则N(u,v)/H(u,v)的值比较大，很容易支配F(u,v)的估计值。解决这个问题的一种方法是限制滤波的频率，从频谱图可知，高频份量的值接近0，而H(0,0)在频率域中一般是H(u,v)的最高值。所以可缩短滤波半径，使经过的频率接近原点，减小遇到零值的几率。spa

直接逆滤波的MATLAB代码以下code

image_o=imread(‘C:\Program Files\MATLAB\R2013a\bin\work\图像复原\lena.bmp’);

subplot(1,3,1);

imshow(image_o);

title(‘原图像’);

%频率域退化图像，退化函数H(u,v)=exp(-0.0025*( (u-M/2).^2+(v-N/2).^2).^(5/6) )

%傅里叶变换

f=im2double(image_o);

F=fft2(f);

F=fftshift(F);

%执行退化

[M,N]=size(F);

[u,v]=meshgrid(1:M,1:N);%生成二维坐标系

H=exp(-0.0025* ( (u-M/2).^2+(v-N/2).^2).^(5/6) );

F=F.*H;

%傅里叶反变换

X=ifftshift(F);

x=ifft2(X);

x=uint8(abs(x)*256);

subplot(1,3,2);

imshow(x);

%

title(‘退化图像’);

image_d=imread(‘C:\Program Files\MATLAB\R2013a\bin\work\图像复原\lena_deterioration.bmp’);

%直接逆滤波图像复原

ff=im2double(image_d);%将图像灰度值归一化到0-1之间

% 傅里叶变换

f_Id=fft2(ff);

f_Id=fftshift(f_Id);

fH_Id=f_Id;

[M,N]=size(fH_Id);

% 逆滤波

threshold=78;

if threshold>M/2

%全滤波

fH_Id=fH_Id./(H+eps);

else

%对必定半径范围内进行滤波

for i=1:M

for j=1:N

if sqrt((i-M/2).^2+(j-N/2).^2)

fH_Id(i,j)=fH_Id(i,j)./(H(i,j)+eps);

end

end

end

end

% 执行傅立叶逆变换

fH_Id1=ifftshift(fH_Id);

f_new=ifft2(fH_Id1);

f_new=uint8(abs(f_new)*255);

subplot(1,3,3);

imshow(f_new);

title(‘滤波半径=78的逆滤波复原图像’);

效果以下

bc82b2ba94b99cf9b2d1f20c2445f250.png

e29da16c77c5ae0c6f4456d459f3491d.png

f72e0d3f7e538fe449f0cc105101e431.png

6cf6193fae60522802854138bdc1afc2.png

从实验结果可知，滤波为78比较适宜。blog