在学习有限元的过程中经常会出现拉格朗日描述、欧拉描述,拉格朗日描述又分为完全的拉格朗日格式、更新的拉格朗日格式,初学者很容易被这些描述和格式类型搞的晕头转向,因此有必要理清它们之间的关系。
引言
描述连续体的变形和响应有两种方式,即拉格朗日描述和欧拉描述。独立变量是材料坐标和时间的描述称为材料描述或拉格朗日描述;独立变量是空间坐标和时间的描述称为空间描述或欧拉描述。
通过对一维问题动量方程的弱形式进行对比,来区分和理解各种格式。
1 材料坐标和空间坐标
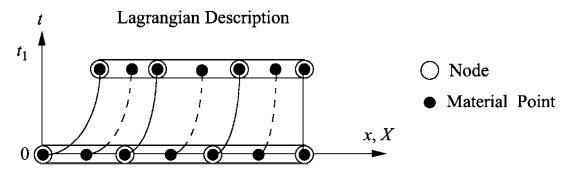
材料坐标用X表示,也称为拉格朗日坐标,材料坐标标记一个材料点,下图为朗格朗日描述,即节点始终与材料点重合,单元之间无材料流动。
空间坐标用x表示,也称为欧拉坐标,空间坐标指一点在空间中的位置,下图为欧拉描述,即节点始终与空间点重合,此时节点位置在空间上固定,材料点在单元中流动。

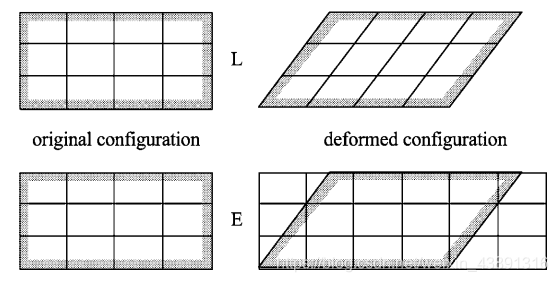
拉格朗日网格和欧拉网格,拉格朗日网格就像刻画在材料上,网格随着材料运动;欧拉网格刻画在空间上,不随材料运动,材料可在网格内流动。
2 欧拉描述
独立变量为空间坐标x和时间t,相关变量表示为空间坐标x和时间t的函数

控制方程,以动量方程为对象
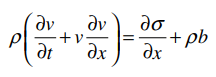
通过对动量方程两端乘变分函数,并在空间域上积分,经过分部积分得到动量方程的弱形式
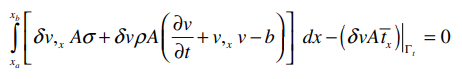
3 拉格朗日描述
在拉格朗日有限元的发展中,一般有两种方法:
1、完全的拉格朗日格式,
2、更新的拉格朗日格式
完全的拉格朗日格式中,在初始构型上描述变量,而更新的拉格朗日格式中,在当前构型上描述变量
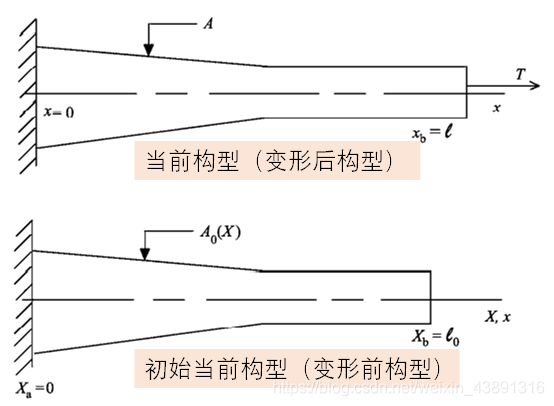
3.1 完全的拉格朗日格式
独立变量为材料坐标X和时间t,相关变量名义应力P和位移u表示为材料坐标X和时间t的函数
动量方程
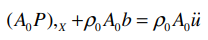
动量方程的弱形式
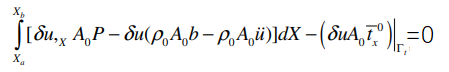
3.2 更新的拉格朗日格式
独立变量为材料坐标X和时间t,相关变量柯西应力和速度表示为材料坐标X和时间t的函数

动量方程
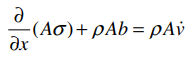
动量方程的弱形式
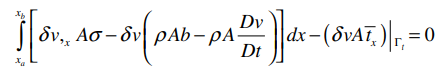
在更新的拉格朗日格式中,动量方程涉及的导数对应于欧拉坐标,而在完全的拉格朗日格式中涉及的导数对应于拉格朗日坐标。
4 总结
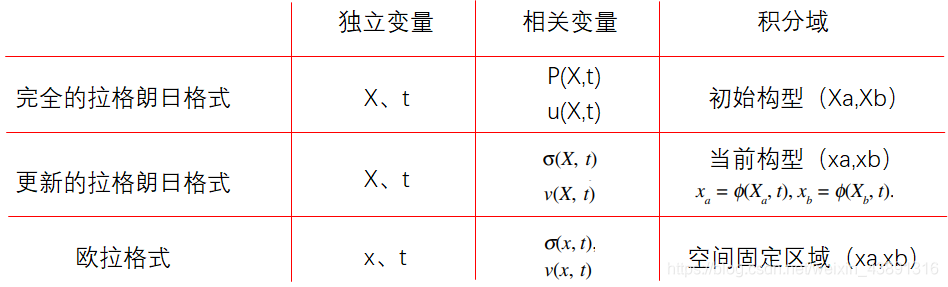
对比三种格式的动量方程弱形式,可以发现更新的拉格朗日和欧拉格式形式基本相同,很容易混淆,为了分清每种格式,需要从独立变量、相关变量、以及积分域进行区分。
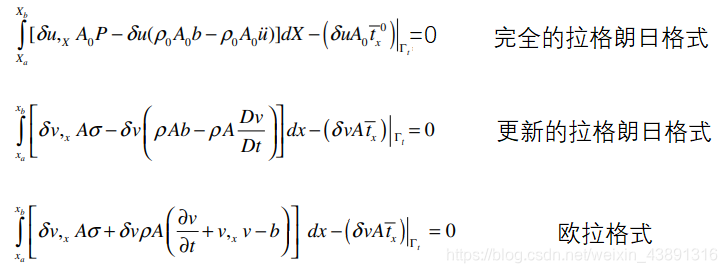
下图中可以看出,拉格朗日格式的独立变量为材料坐标和时间,完全的拉格朗日格式积分域为初始构型,更新的拉格朗日积分域为当前构型;欧拉格式的独立变量为空间坐标和时间,积分域为空间固定区域,这里更新的拉格朗日和欧拉的积分域都写为(xa,xb),二者都是空间坐标,但物理意义不同,更新的拉格朗日积分限为初始构型(Xa,Xb)变形后对应的空间坐标,而欧拉格式的积分限(xa,xb)为欧拉网格对应的固定的空间域。