Boyer-Moore字符串匹配算法

Boyer-Moore字符串匹配算法

一、算法简介

在计算机科学中，Boyer-Moore字符串搜索算法是一种非常高效的字符串搜索算法。它由德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授设计于1977年。
算法的流程是从后往前依次比较模式串和主串中的字符，利用好字符和坏字符来计算模式串的偏移量。
在上面的描述中，有几个概念需要先了解：
主串与模式串：
例如：我们要在字符串“abcacabdc”中查找字符串“abd”，那么我们称“abcacabdc” 叫做主串；“abd”叫做模式串。

坏字符：
在Boyer-Moore简称BM算法中，模式串中的字符与主串进行匹配时是按照从后往前的次序进行匹配的。在下图中，模式串的字符d与主串的字符进行比对，发现不匹配，那么我们称主串中第一个与模式串不相等的字符叫做坏字符

此时，我们将坏字符 c 对应模式串字符的位置，记作 i，那么此时 i = 2 （从0开始计算）

好后缀：
对于主串和模式串来说，碰到坏字符之前所匹配到的字符串称为好后缀

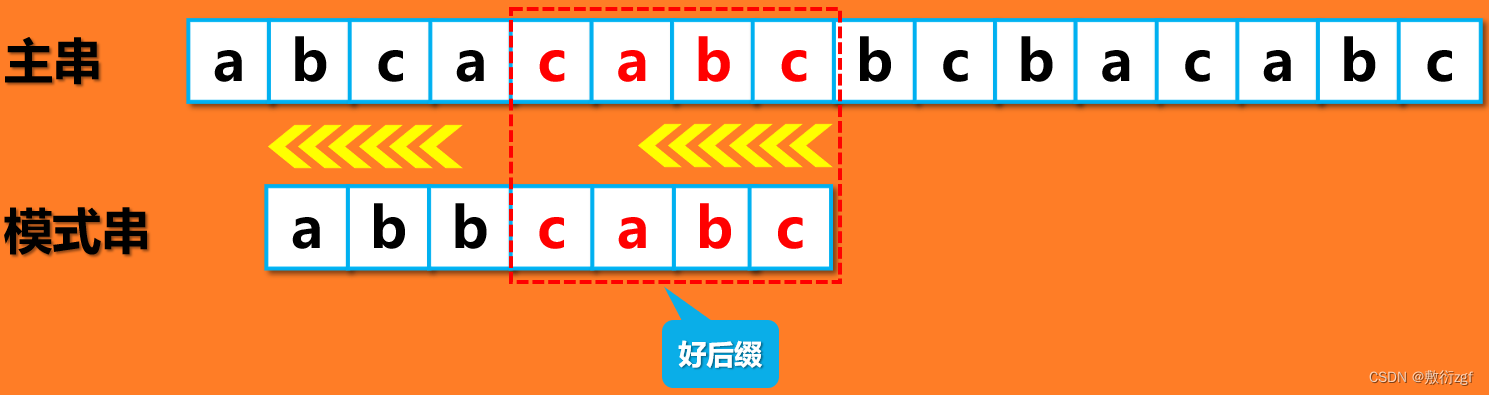
二、模式串的移动

（一）坏字符

首先，我们讲解坏字符的情况，对于第二幅图来说，模式串应该向后移动几位呢？
流程是这样的：我们在模式串中查找坏字符的位置（从后向前找到第一个与之匹配的字符），将其位置记为 k （k 的默认值为 -1 ，表示模式串中不存在坏字符），那么模式串向后移动的位数为 i – k 位。

如图，我们要在模式串中找到坏字符 c ，发现并没有， 因此模式串向后移动 i – k=2-（-1）=3 位

此时，主串中的坏字符 a 所对应的 i 值仍然为 2，所以开始在模式串中寻找第一个与 a 匹配的字符，找到了，k = 0，因此，模式串向后移动 i – k = 2 – 0 = 2 位

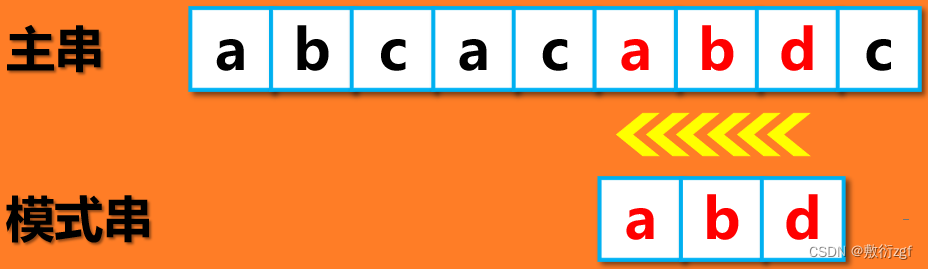
这样就匹配成功啦 ！！

（二）好后缀

在上面的案例中，我们似乎觉得采用坏字符的方法就能够完成模式串的匹配操作，但实际上会遇到下面这种情况。

假设主串不发生变化，模式串变为 “dbca” ，此时坏字符为 a ，对应模式串中 i = 0 ，模式串中包含坏字符 k = 3 ，那么模式串需要向后移动 i – k = 0 – 3 = -3 位，也就是向前移动 3 位，这样明显是不可取的，因此我们仅仅采用坏字符来完成模式匹配是不够用的。
那么对于好后缀来说，不同的情形对应不同的移动方式：
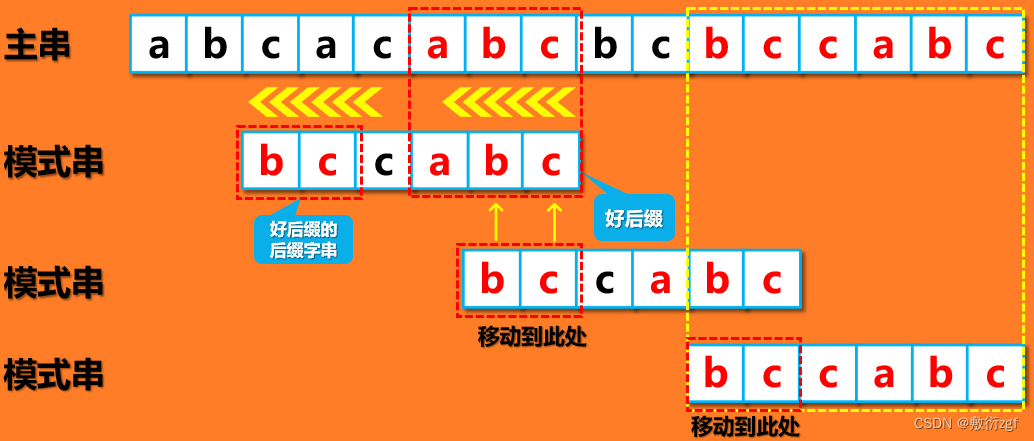
情形一： 在模式串中寻找，是否还有与好后缀一样的字符串，如果有的话将其向后移动到之前好后缀的位置。

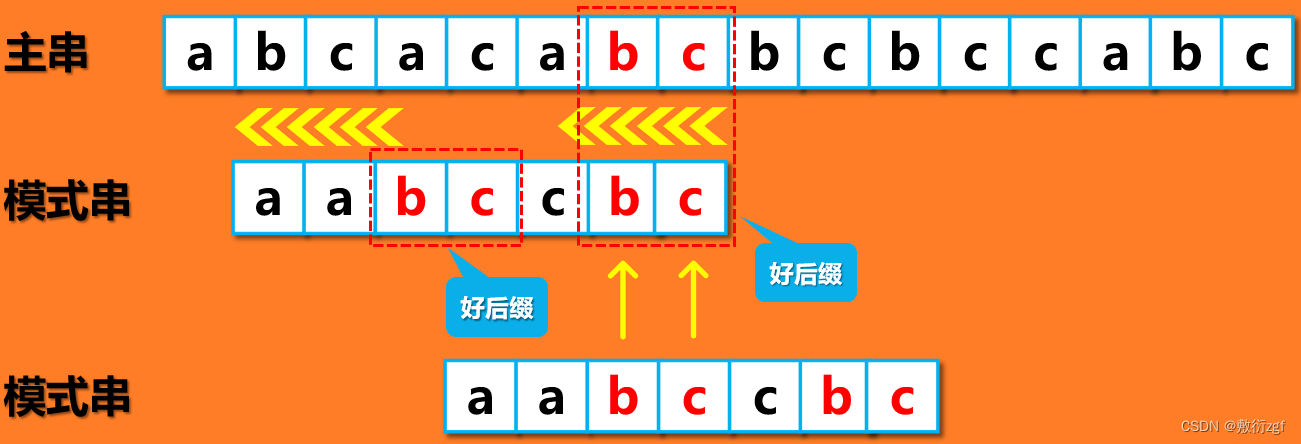
情形二： 模式串中没有与好后缀一样的字符串
此时好后缀 abc 的后缀子串 bc 正好跟模式串的前缀子串 bc 一致，那么就将模式串中前缀子串移动到好后缀的 bc 处，移动位数： i = 5 – 1 = 4 位 ；若好后缀规则没有匹配到，则按默认值 -1 移动，如下

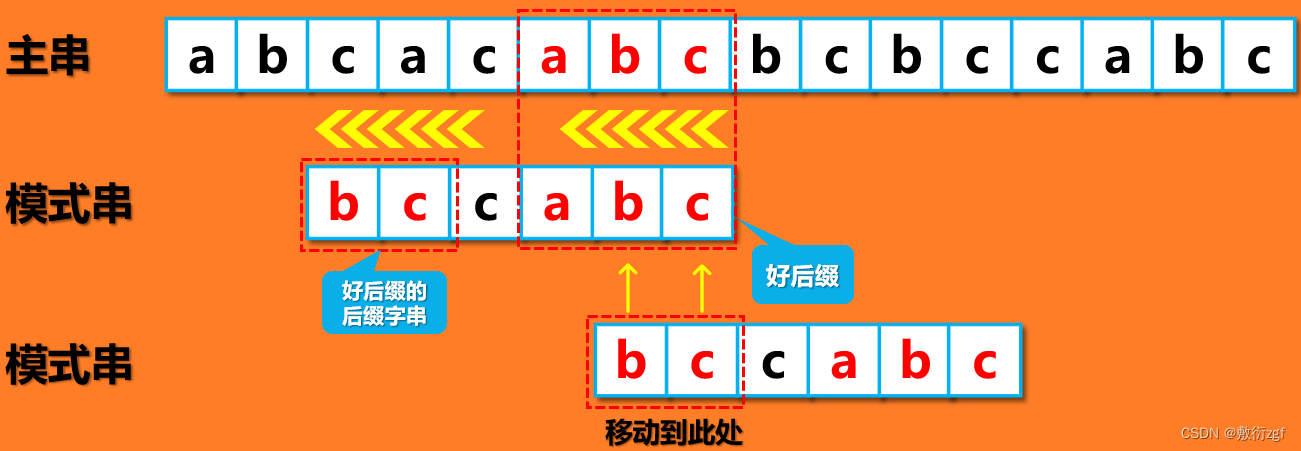
在上述案例中，讲到了好后缀的后缀子串、以及模式串的前缀子串，那么怎么理解呢？举个栗子：例如我们的模式串“bccabc”中，好后缀为“abc”，那么它的后缀字串为“bc”或者“c”；模式串的前缀子串为“bc”或者“b”，其中需要注意的是：选取的后缀字串长度要和模式串的前缀子串相等。 也就是说，若选取后缀字串为bc，那么前缀子字串只能为bc ，不能为b。
同理，好后缀为bc，模式串中有和好后缀一样的字符，将其移动到好后缀的位置，整个模式串匹配成功。

（三）坏字符与好后缀规则综合考虑

好了，这样我们就了解了好后缀和坏字符的移动规则，但也面临一个新的问题，在实际操作过程中，我们该如何选择呢？
在实际的匹配过程中，需要将二者结合使用，计算出坏字符规则的移动位数，再算出好后缀规则的移动位数取较大的作为真正的向后移动位数，保证最高效率的匹配。如下图：

可以看到，坏字符对应的 i = 5，k = 3，采用坏字符规则，模式串向后移动 5 – 3 = 2位；
好后缀规则没有匹配到，则模式串向后移动2位。

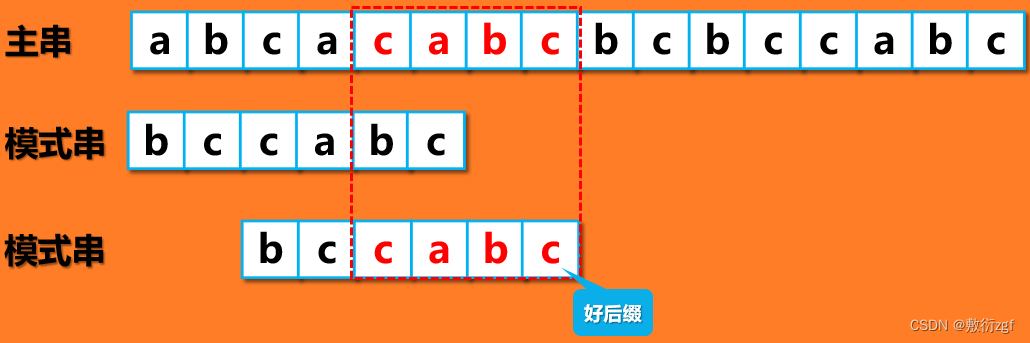
移动2位后，匹配到了好后缀“cabc”，按照好后缀规则，模式串移动5 – 1 = 4 位；按照坏字符规则（坏字符为 a ，对应 i = 1，由于模式串中a 对应k = 3），模式串移动 i – k = -2 ，选取较大的好后缀移动模式，向后移动4位。

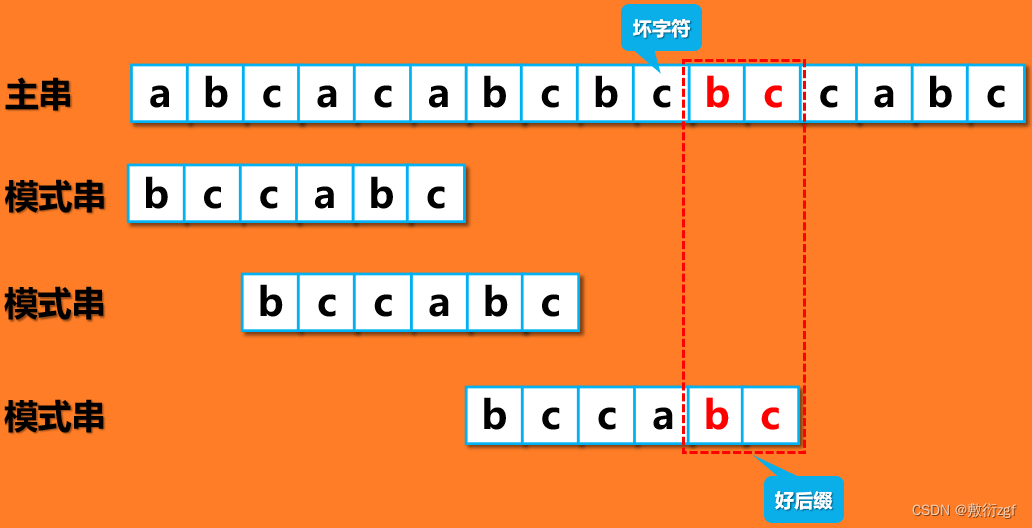
移动后好后缀位 bc ，坏字符为 c ，按照好后缀规则，模式串向后移动 5 – 1 = 4位；按照坏字符规则，模式串向后移动 2 – 5 = -3位，因此选择好后缀规则。

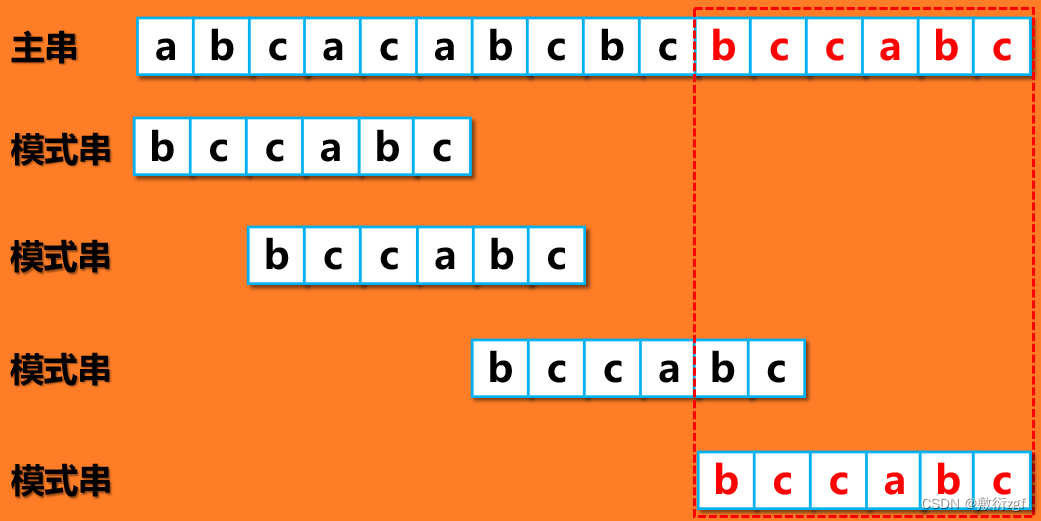
匹配成功！

三、代码实现

def find_boyer_moore(text, pattern):
    """如果模式串pattern存在text中，则返回pattern在text中起始位置索引，否则返回-1"""
    n, m = len(text), len(pattern)
    if m == 0: # 模式串长度为0
        return 0
    last = {}
    for k in range(m):  # 以pattern中字符为键 索引为值创建字典   
        last[pattern[k]] = k
    print(last) # 出现重复字符，则以最后一次出现的索引为值
    # 初始化索引辅助变量，使得pattern最右侧字符和text索引m-1处对齐 （从模式串的最右侧开始比对）
    i = m - 1 # 15
    k = m - 1
    while i < n: # 没有对比到主串的末尾
        print(text[i])
        print(pattern[k])
        print("========")
        if text[i] == pattern[k]:
            if k == 0:  # 判断是否连续完成了len(pattern)次成功匹配
                return i  # 成功将pattern和text某子串进行匹配后，text中和pattern相同的子串起始于索引i
            else:  # 继续从右向左比对pattern和text对齐位置字符相同
                i -= 1
                k -= 1 # 成功比对一次 i和K就减一，直至 k = 0 表示比对完毕
        else: # 表示该次比对没有成功
            j = last.get(text[i], -1) # j 表示模式串中坏字符的索引
            print("j:" + str(j))
            if j < k:  # text[i]坏字符不存在pattern中即j = -1时，该条件及其操作依然成立
                i += m - (j + 1)  # 模式串中坏字符第一次出现在坏字符对应在模式串中字符的前面，那么模式串需要移动k-j位，i 则需要递增 k-j + (m - k -1) 由于m表示长度，-1才能和下标对应
            if j > k:
                i += m - k  # 模式串中坏字符第一次出现在坏字符对应在模式串中字符的后面，那么模式串需要移动1位，i递增1 +(m-k-1)
            k = m - 1  # 重新从右开始对pattern和text进行匹配
    return -1


if __name__ == '__main__':
    # 主串
    text = 'I love Natural language processing'
#     text = 'ABCDABCD'
    # 模式串
    pattern = 'Natural language'# 15
#     pattern = 'DAC'# 15
    print("返回模式串的第一个字符在主串中的位置：" + str(find_boyer_moore(text, pattern)))