一、引入
GraphSLAM是解决完整的slam问题的slam算法。这意味着该算法将恢复整个路径和地图,而不仅仅是最近的姿势和地图。这种差异使它可以考虑当前姿势与先前姿势之间的依赖性。适用于我们的GraphSLAM的一个示例是地下采矿。每天都用在钻孔机上的大型机器在岩壁上切割。环境瞬息万变,保持正确的工作空间图非常重要。映射此空间的一种方法是在周围环境中驾驶装有激光雷达的车辆并收集有关周围环境的数据。
GraphSLAM 算法解决了全SLAM 问题。该算法旨在解决定义在所有位姿和地图中所有特征上的离线问题。
二、GraphSLAM模型
1. 最大似然估计
GraphSLAM的核心是图形优化-将图形中所有约束中存在的错误最小化的过程。让我们看一下这些约束,并学习应用称为最大似然估计(MLE)的原理来构造和解决图形的优化问题。
(1)特征量测示例
让我们看一个非常简单的示例-我们的机器人在环境中重复测量功能的一个示例。本示例将引导您完成解决该问题所需的步骤,然后可以将其应用于更复杂的问题。
机器人的初始姿态的方差为0-仅仅是因为这是机器人的起始位置。回想一下开始位置可能在哪里-我们在相对地图中将其称为位置0。此后的每个动作姿势和测量都不确定。在GraphSLAM中,我们将继续假设运动和测量数据具有高斯噪声。
机器人测量一个特征,
m
1
m_1
m1,返回距离为1.8米。
如果我们将这个特征类比做弹簧——1.8米是弹簧的静止长度。这是弹簧最理想的长度。然而,弹簧有可能被压缩或拉长,以适应作用于系统的其他力(约束)。
这种测量的概率分布可以定义为,
p
(
x
)
=
1
σ
2
π
e
−
1
2
(
z
1
−
(
x
0
+
1.8
)
)
2
σ
2
p(x)=\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}\frac{(z_1−(x_0+1.8))^2}{σ^2}}
p(x)=σ2π1e−21σ2(z1−(x0+1.8))2
简单地说,当
z
1
z_1
z1和
x
0
x_0
x0相距1.8米时,概率分布最高。

然而,由于位置的第一个姿势,
x
0
x_0
x0设为0,这一项可以简单地从方程中移除。
p
(
x
)
=
1
σ
2
π
e
−
1
2
(
z
1
−
1.8
)
2
σ
2
p(x)=\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}\frac{(z_1−1.8)^2}{σ^2}}
p(x)=σ2π1e−21σ2(z1−1.8)2
接下来,机器人对环境中的相同特征进行另一次测量。这次,数据读取为2.2m。由于存在两个相互矛盾的测量结果,因此这是一个超定的系统-因为方程式多于未知数。
通过两次测量,可以通过两个概率的乘积来表示特征的最可能位置。
p
(
x
)
=
1
σ
2
π
e
−
1
2
(
z
1
−
1.8
)
2
σ
2
×
1
σ
2
π
e
−
1
2
(
z
1
−
2.2
)
2
σ
2
p(x)=\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}\frac{(z_1−1.8)^2}{σ^2}}\times\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}\frac{(z_1−2.2)^2}{σ^2}}
p(x)=σ2π1e−21σ2(z1−1.8)2×σ2π1e−21σ2(z1−2.2)2
在这个简单的示例中,所以我们可以猜测
z
1
z_1
z1最有可能出现的位置是在2.0米处。然而,通过最大似然估计过程来理解所涉及的步骤是有价值的,然后才能将其应用于更复杂的系统。
要解析地解决这个问题,可以采取几个步骤把方程简化成更简单的形式。
删除比例系数
使方程式最大化的m值不取决于每个指数前面的常数。这些是比例系数,但是在SLAM中,我们通常对概率的绝对值不感兴趣,而是找到最大似然估计。因此,可以我们可以简单地消除这些系数。
p
(
x
)
=
e
−
1
2
(
z
1
−
1.8
)
2
σ
2
×
e
−
1
2
(
z
1
−
2.2
)
2
σ
2
p(x)=e^{-\frac{1}{2}\frac{(z_1−1.8)^2}{σ^2}}\times e^{-\frac{1}{2}\frac{(z_1−2.2)^2}{σ^2}}
p(x)=e−21σ2(z1−1.8)2×e−21σ2(z1−2.2)2
对数似然函数
概率的乘积已被简化,但方程仍然相当复杂——存在指数函数。这里有一个数学性质可以用来把指数的乘积转换成指数的和。
首先,我们必须使用下面的性质,
e
a
e
b
=
e
a
+
b
e^ae^b=e^{a+b}
eaeb=ea+b,把两个指数合并成一个。
e
−
1
2
(
z
1
−
1.8
)
2
σ
2
×
e
−
1
2
(
z
1
−
2.2
)
2
σ
2
=
e
−
1
2
(
z
1
−
1.8
)
2
σ
2
−
1
2
(
z
1
−
2.2
)
2
σ
2
e^{-\frac{1}{2}\frac{(z_1−1.8)^2}{σ^2}}\times e^{-\frac{1}{2}\frac{(z_1−2.2)^2}{σ^2}} = e^{-\frac{1}{2}\frac{(z_1−1.8)^2}{σ^2}-\frac{1}{2}\frac{(z_1−2.2)^2}{σ^2}}
e−21σ2(z1−1.8)2×e−21σ2(z1−2.2)2=e−21σ2(z1−1.8)2−21σ2(z1−2.2)2
接下来,我们不用自然对数,而是取其自然对数并对其进行处理。
ln
(
e
−
1
2
(
z
1
−
1.8
)
2
σ
2
×
e
−
1
2
(
z
1
−
2.2
)
2
σ
2
)
=
−
1
2
(
z
1
−
1.8
)
2
σ
2
−
1
2
(
z
1
−
2.2
)
2
σ
2
\ln (e^{-\frac{1}{2}\frac{(z_1−1.8)^2}{σ^2}}\times e^{-\frac{1}{2}\frac{(z_1−2.2)^2}{σ^2}} )= {-\frac{1}{2}\frac{(z_1−1.8)^2}{σ^2}-\frac{1}{2}\frac{(z_1−2.2)^2}{σ^2}}
ln(e−21σ2(z1−1.8)2×e−21σ2(z1−2.2)2)=−21σ2(z1−1.8)2−21σ2(z1−2.2)2
自然对数是一个单调函数——在对数的情况下——它总是递增的——如下图所示。它的值只能有一个一对一的映射。这意味着优化可能性的对数与最大化可能性本身没有什么不同。
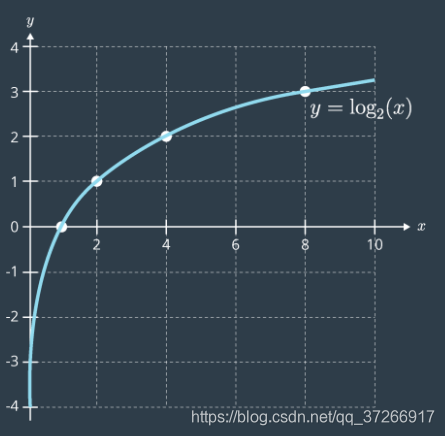
处理似然记录时要注意的一件事是,它们始终是负数。这是因为概率假定值为0到1之间,并且0到1之间的任何值的对数均为负。可以在上图中看到。出于这个原因,与数似然工作时,优化限嗣继承减少的负对数似然; 而在过去,我们试图将可能性最大化。
最后,如之前所做的那样,可以无条件删除等式前面的常数。同样,出于本示例的目的,我们将假设在获得两个测量值时使用了相同的传感器-因此将忽略方程式中的方差。
(
z
1
−
1.8
)
2
+
(
z
1
−
2.2
)
2
(z_1 −1.8)^2 +(z_1−2.2) ^2
(z1−1.8)2+(z1−2.2)2
优化
在这一点上,方程已经大大简化了。为了得到它的最简形式,剩下的就是把所有项相乘。
2
z
1
2
−
8
z
1
+
8.08
2z_1^2−8z_1+8.08
2z12−8z1+8.08
为了找到这个方程的最小值,你可以对方程求一阶导数并令它等于0。
4
z
1
−
8
=
0
4
z
1
=
8
z
1
=
2
4z_1−8=0\\ 4z_1 = 8\\ z_1 = 2
4z1−8=04z1=8z1=2
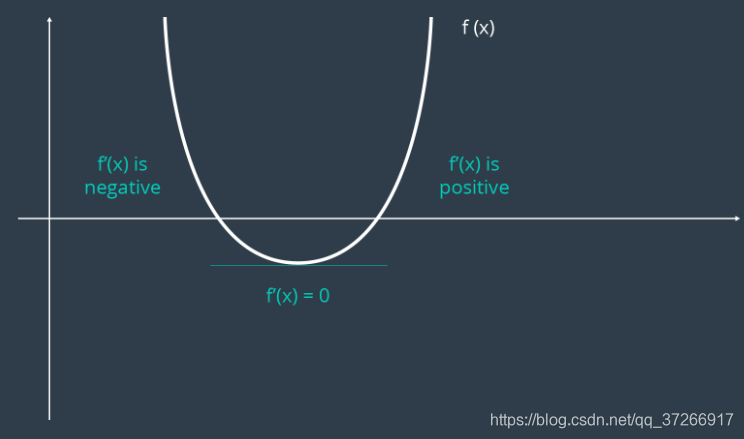
通过这样做,可以轻易地找到曲线上的位置,其中的斜率(或梯度,在多维方程中)等于零即波谷。通过查看错误函数的图形,可以很容易地可视化此属性。
总览
这里执行的过程是MLE问题的解析解。包括的步骤:
- 删除无关紧要的常数,
- 将一个似然估计的方程转换为负对数似然估计的方程
- 计算函数的一阶导数并使其等于零,从而求出极值。
在GraphSLAM中,前两个步骤可以应用于每个约束。因此,任何测量或运动约束都可以简单地标记为负对数似然误差。对于一个度量约束,这类似于以下,
(
z
t
−
(
x
t
+
m
t
)
)
2
σ
2
\frac{(z_t−(x_t+m_t))^2}{σ^2}
σ2(zt−(xt+mt))2
对于运动约束,
(
x
t
−
(
x
t
−
1
+
u
t
)
)
2
σ
2
\frac{(x_t−(x_t−1+u_t))^2}{σ^2}
σ2(xt−(xt−1+ut))2
因此,约束将被标记为负对数似然误差,

估计函数试图最小化所有约束的和,
J
G
r
a
p
h
S
L
A
M
=
∑
t
(
x
t
−
(
x
t
−
1
+
u
t
)
)
2
σ
2
+
∑
t
(
z
t
−
(
x
t
+
m
t
)
)
2
σ
2
J_{GraphSLAM}=∑_{t}\frac{(x_t−(x_t−1+u_t))^2}{σ^2}+∑_t\frac{(z_t−(x_t+m_t))^2}{σ^2}
JGraphSLAM=t∑σ2(xt−(xt−1+ut))2+t∑σ2(zt−(xt+mt))2
(2)MLE的数值解
在更复杂的问题中,找到解析解可能需要冗长的计算。幸运的是,还有另一种选择-可以在短时间内找到最大似然问题的数值解。我们将探讨上一个示例的数值解决方案。
数值解
下例显示了误差函数的图形。在此示例中,很容易看到全局最小值位于何处。但是,在具有多个维度的更复杂的示例中,这并不简单。

可以通过应用优化算法来数值求解此MLE。优化算法的目标是快速找到最佳解决方案-在这种情况下为局部最小值。有几种不同的算法可以解决这个问题。在SLAM中,梯度下降,Levenberg-Marquardt和共轭梯度算法非常普遍。
梯度下降算法
回想一下,函数的梯度是指向最大变化率方向的矢量;或在极端情况下等于零。
在梯度下降中-进行初始猜测,然后沿与梯度相反的方向进行增量调整。最终,应该达到最低限度的功能。
该算法确实有一个缺点-在复杂的分布中,初始猜测可能会显着改变最终结果。根据最初的猜测,该算法收敛于两个不同的局部最小值。该算法无法确定全局最小值在哪里-它沿最陡的坡度向下移动,并且当达到局部最小值时,它认为其任务已完成。解决此问题的一种方法是使用随机梯度下降算法(SGD)。
2. 一维到多维
在前面的示例中,您正在使用一维图。机器人的运动和测量仅限于一维-它们可以向前或向后执行。
(1)1-Dimensional Graphs
在这种情况下,每个约束可以用以下形式表示:
1-D 测量约束:
(
z
t
−
(
x
t
+
m
t
)
)
2
σ
2
\large \frac{(z_t – (x_t + m_t))^2}{\sigma^2}
σ2(zt−(xt+mt))2
1-D 运动约束:
(
x
t
−
(
x
t
−
1
+
u
t
)
)
2
σ
2
\large \frac{(x_t – (x_{t-1} + u_t))^2}{\sigma^2}
σ2(xt−(xt−1+ut))2
(2)n-Dimensional Graphs
在多维系统中,我们必须使用矩阵和协方差来表示约束。这种概括可以应用于二维,三维和实际上任何n个维的系统。约束方程看起来像这样,
n-D 测量约束:
(
z
t
−
h
(
x
t
,
m
j
)
)
T
Q
t
−
1
(
z
t
−
h
(
x
t
,
m
j
)
)
(
z
t
−
h
(
x
t
,
m
j
)
)
(z_t-h(x_t,m_j))^TQ_t^{-1}(z_t-h(x_t,m_j))(zt−h(xt,mj))
(zt−h(xt,mj))TQt−1(zt−h(xt,mj))(zt−h(xt,mj))
n-D 运动约束:
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
T
R
t
−
1
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
(x_t-g(u_t,x_{t-1}))^TR_t^{-1}(x_t-g(u_t,x_{t-1}))(xt−g(ut,xt−1))
(xt−g(ut,xt−1))TRt−1(xt−g(ut,xt−1))(xt−g(ut,xt−1))
其中
h
(
)
h()
h()和
g
(
)
g()
g()表示测量和运动函数,
Q
t
Q_t
Qt和
R
t
R_t
Rt为测量和运动噪声的协方差。
所有约束的和的多维公式如下所示。
J
G
r
a
p
h
S
L
A
M
=
x
0
T
Ω
x
0
+
∑
t
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
T
R
t
−
1
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
+
∑
t
(
z
t
−
h
(
x
t
,
m
j
)
)
T
Q
t
−
1
(
z
t
−
h
(
x
t
,
m
j
)
)
J_{GraphSLAM} = x_0^T \Omega x_0 + \sum_t(x_t-g(u_t,x_{t-1}))^T R_t^{-1}(x_t-g(u_t,x_{t-1}))\\ \quad + \sum_t(z_t-h(x_t,m_j))^TQ_t^{-1}(z_t-h(x_t,m_j))
JGraphSLAM=x0TΩx0+t∑(xt−g(ut,xt−1))TRt−1(xt−g(ut,xt−1))+t∑(zt−h(xt,mj))TQt−1(zt−h(xt,mj))
sum中的第一个元素是初始约束—它将第一个机器人姿态设置为与地图的原点相等。协方差
Ω
0
\Omega_0
Ω0表示完全置信度。
本质上,
Ω
0
=
[
∞
0
0
0
∞
0
0
0
∞
]
\Omega_0 = \begin{bmatrix} \infty &0 & 0 \\ 0 & \infty & 0\\ 0 & 0 & \infty \end{bmatrix}
Ω0=⎣⎡∞000∞000∞⎦⎤
既然我们正在处理多维图和多维约束,那么使用更智能的数据结构来处理我们的数据就很有意义。
三、GraphSLAM算法
个人认为课程在这个部分讲的不是太清楚,可能因为其避免涉及比较复杂的公式和推导。但是我觉得模型还是比较重要的,所以我将在这个部分会整合《概率机器人》中的内容。
1.《概率机器人》
2. 无处不在的小土翻译版
1. 算法思想
GraphSLAM背后的思想非常简单,从数据中提取软约束,并将之用稀疏图的形式表示出来。它通过将这些约束转换到全局的关联度估计,从而获得地图和机器人的路径。这些约束通常都是非线性的, 但在求解它们的时候都要对其线性化,将之转换为信息矩阵的形式。因此GraphSLAM本质上是基于信息论的技术。我们将从两个方面来讨论GraphSLAM:构建具有非线性约束的稀疏图、 线性化约束的稀疏信息矩阵。
(1)建立图形
假设我们有一组测量值
z
1
:
t
z_{1:t}
z1:t及其对应的关联度变量
c
1
:
t
c_{1:t}
c1:t,以及控制量集合
u
1
:
t
u_{1:t}
u1:t。GraphSLAM将这些数据转换为图,图中的节点就是机器人的位姿
x
1
:
t
x_{1:t}
x1:t, 以及地图的特征
m
=
m
j
m = {m_j}
m=mj。图中的每一条边都对应着一个事件,运动事件生成一条连接着两个机器人位姿的边,测量事件则在位姿和地图中的特征之间构建了边。 边表示GraphSLAM中位姿和特征之间的软约束。
对于一个线性系统,这些约束对应着大系统方程中的信息矩阵和信息向量的元素。按照惯例,令
Ω
\Omega
Ω表示信息矩阵,
ξ
\xi
ξ表示信息向量。后面我们会提到, 每个测量值和控制量都会对
Ω
\Omega
Ω和
ξ
\xi
ξ进行一次局部更新(local update),其表现形式就是在图中增加了一条边。 实际上,将控制量和测量值整合进
Ω
\Omega
Ω和
ξ
\xi
ξ的规则就是局部地增加,在一定程度上将信息表示为一种增量(additive quantity)。
图3.1.1a. 观测到路标
m
1
m_1
m1
图3.1.1举例说明了构建图及其信息矩阵的过程。首先考虑一个测量值
z
t
i
z_t^i
zti,它提供了
t
t
t时刻机器人位姿
x
t
x_t
xt和特征
j
=
c
t
i
j = c_t^i
j=cti之间的信息。 在GraphSLAM中这一信息会被表述为
x
t
x_t
xt和
m
j
m_j
mj之间的一个约束。我们可以将这个边看作是弹簧-质块模型(spring-mass model)中的弹簧,约束形式为
(
z
t
i
−
h
(
x
t
,
m
j
)
)
T
Q
t
−
1
(
z
t
i
−
h
(
x
t
,
m
j
)
)
\left(z_t^i – h(x_t, m_j) \right)^T Q_t^{-1} \left(z_t^i – h(x_t, m_j) \right)
(zti−h(xt,mj))TQt−1(zti−h(xt,mj)) 其中
h
h
h是已经很熟悉的测量方程,
Q
t
Q_t
Qt则是测量噪声中的协方差。图3.1.1a中显示了GraphSLAM将这样的一条边添加进图的过程。
现在考虑机器人的运动。控制量
u
t
u_t
ut提供了
t
−
1
t-1
t−1时刻和
t
t
t时刻机器人的相对位置关系的信息。这一信息可以以如下的形式作为一个约束添加到图中:
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
T
R
t
−
1
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
\left(x_t – g(u_t, x_{t-1}) \right)^T R_t^{-1} \left(x_t – g(u_t, x_{t-1}) \right)
(xt−g(ut,xt−1))TRt−1(xt−g(ut,xt−1)) 其中,
g
g
g就是机器人运动学模型,
R
t
R_t
Rt则是运动噪声的协方差。如图3.1.1b所示,添加一个这样的边到图中。 图中还显示了在信息矩阵中新增的从位姿
x
t
−
1
x_{t-1}
xt−1到
x
t
x_t
xt之间的元素。这个更新过程也是增量的。这一数值反映了因为运动噪声
R
t
R_t
Rt而残存的不确定度。噪声越小, 添加到
Ω
\Omega
Ω和
ξ
\xi
ξ的数值就越大。
图3.1.1b. 从
x
1
x_1
x1到
x
2
x_2
x2的机器人运动
综合了所有的测量值
z
1
:
t
z_{1:t}
z1:t和控制量
u
1
:
t
u_{1:t}
u1:t,我们就得到了软约束形式的稀疏图。图中约束的数量随着时间线性的增长,因此所得的图是稀疏的。图中所有约束的和为:
J
G
r
a
p
h
S
L
A
M
=
x
0
T
Ω
0
x
0
+
∑
t
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
T
R
t
−
1
(
x
t
−
g
(
u
t
,
x
t
−
1
)
)
+
∑
t
∑
i
(
z
t
i
−
h
(
x
t
,
c
t
i
)
)
T
Q
t
−
1
(
z
t
i
−
h
(
x
t
,
c
t
i
)
)
J_{\mathrm{GraphSLAM}} = x_0^T \Omega_0 x_0 + \sum_t \left(x_t – g(u_t, x_{t-1}) \right)^T R_t^{-1} \left(x_t – g(u_t, x_{t-1}) \right) \\+ \sum_t \sum_i \left(z_t^i – h(x_t, c_t^i) \right)^T Q_t^{-1} \left(z_t^i – h(x_t, c_t^i) \right)
JGraphSLAM=x0TΩ0x0+t∑(xt−g(ut,xt−1))TRt−1(xt−g(ut,xt−1))+t∑i∑(zti−h(xt,cti))TQt−1(zti−h(xt,cti))
它是定义在位姿变量
x
1
:
t
x_{1:t}
x1:t以及地图
m
m
m中所有的特征上的函数。注意到这一表达式还有一个形如
x
0
T
Ω
0
x
0
x_0^T \Omega_0 x_0
x0TΩ0x0的硬约束(anchoring constrains)。 该约束通过将机器人的初始位姿初始化为
(
0
0
0
)
T
\begin{pmatrix} 0 & 0 & 0 \end{pmatrix}^T
(000)T来固定地图的绝对坐标。
图3.1c. 几步之后的约束
在相关的信息矩阵
Ω
\Omega
Ω中,非对角元素都为0, 但有两个例外。
- 任何两个邻接的位姿状态
x
t
−
1
x_{t-1}
xt−1和x
t
x_t
xt对应着一个非零的值, 表示由控制量u
t
u_t
ut所引入的信息边。 - 如果机器人在位姿
x
t
x_t
xt上能够观测到特征m
j
m_j
mj那么信息矩阵中对应着x
t
x_t
xt–m
j
m_j
mj的元素就是非零的。
若所有的特征对所对应的信息矩阵元素都为0。 这反映了我们从来没有采集到特征之间的相对位置关系,在SLAM中我们采集到的全是测量值信息,约束了机器人和特征之间的位置关系。因此,信息矩阵就是稀疏的, 除了线性数量的元素外其余各元素均为0。
(2) 推论
显然,无论是图的形式还是信息矩阵的形式都可以给我们提供地图和路径信息。在GraphSLAM中地图和路径是通过线性化的信息矩阵
μ
=
Ω
−
1
ξ
μ = \Omega^{-1} \xi
μ=Ω−1ξ获得的。 这个操作要求我们求解一个由线性方程构成的系统。这带来了一个我们该如何高效的恢复地图估计
μ
μ
μ和协方差矩阵
Σ
\Sigma
Σ的问题。
这一复杂问题的答案依赖于世界的拓扑逻辑。如果每个特征都只能在一处看到,那么这个图就是线性约束表示的。那么
Ω
\Omega
Ω就可以通过线性变换写成带对角阵(band-diagonal matrix)的形式, 所有的非零元素都出现在对角元素的两侧。方程
μ
=
Ω
−
1
ξ
μ = \Omega^{-1} \xi
μ=Ω−1ξ就可以在线性的时间里解出。这一思想描述的是只遍历一次的无环世界, 因此每个特征都可以看作是一个短的连续的时间段内的特征。
但是,更一般的情况是同一个特征可能被多次观测到,而且每次观测到的时间间隔很大。这可能是由于机器人在走廊里来来回回的运动,或者世界本身就是有环的。 在任何一种情况下,都有特征
m
j
m_j
mj在两个完全不同的时间点所对应的位姿
x
t
1
,
x
t
2
x_{t_1}, x_{t_2}
xt1,xt2上被观测到,其中
t
2
≫
t
1
t_2 \gg t_1
t2≫t1。在我们的约束图中,这就产生了一个环形依赖,
x
t
1
x_{t_1}
xt1和
x
t
2
x_{t_2}
xt2通过控制序列
u
t
1
+
1
,
u
t
1
+
2
,
⋯
,
u
t
2
u_{t_1 + 1}, u_{t_1 + 2}, \cdots, u_{t_2}
ut1+1,ut1+2,⋯,ut2连接起来,并分别在
x
t
1
x_{t_1}
xt1和
m
j
m_j
mj以及
x
t
2
x_{t_2}
xt2和
m
j
m_j
mj之间建立了观测边。 这些边的存在,使得我们不能通过简单的线性变换得到带对角阵,因此求解地图过程更复杂。实际上,因为
Ω
\Omega
Ω的逆与一个向量相乘,所以其结果可以通过诸如共轭梯度这样的优化算法得到, 而不需要显示的计算一个矩阵的逆。因为实际的实际总是有着各种各样的环,所以这一过程就更有意义了。
GraphSLAM使用了一种称为因式分解(factorization trick)的手段,我们可以将之看作是通过信息矩阵传播的信息,实际上它是著名的求解矩阵逆的消元法的一种推广形式。 假设我们想要从信息矩阵
Ω
\Omega
Ω和信息状态
ξ
\xi
ξ中移除一个特征
m
j
m_j
mj。在弹簧质块的模型中,这就相当于移除一个节点和连接在该节点上的所有边。 后面我们会看到,这可以通过一个十分简单的操作来实现,我们可以通过在任何共有
m
j
m_j
mj的两个位姿节点之间添加一条边,来移除所有
m
j
m_j
mj和观测到
m
j
m_j
mj的位姿节点之间的边。
这一过程如图3.1.2所示,移除了两个地图特征
m
1
m_1
m1和
m
3
m_3
m3,对于这个地图而言移除
m
2
m_2
m2和
m
4
m_4
m4无足轻重。特征的移除修改了观测到特征的位姿对之间的边。 如图3.1.2b所示,这一操作可能会在图中新增边,特征
m
3
m_3
m3的移除在位姿
x
2
x_2
x2和
x
4
x_4
x4之间新增了一条边。

图3.2. GraphSLAM算法中的图化简。移除特征相关的边,只留下了位姿状态之间的边。
正式地,令
τ
(
j
)
\tau(j)
τ(j)为观测到
m
j
m_j
mj的位姿集合(即
x
t
∈
τ
(
j
)
⟺
∃
i
:
c
t
i
=
j
x_t \in \tau(j) \Longleftrightarrow \exists i : c_t^i = j
xt∈τ(j)⟺∃i:cti=j)。那么我们就知道特征
m
j
m_j
mj只与集合
τ
(
j
)
\tau(j)
τ(j)中的位姿有关联。 在构建过程中,
m
j
m_j
mj不再与其它任何位姿或者特征节点有关联。现在我们可以将所有
m
j
m_j
mj与
τ
(
j
)
\tau(j)
τ(j)之间的边都设定为0,并在任何两个节点
x
t
,
x
t
′
∈
τ
(
j
)
x_t, x_{t’} \in \tau(j)
xt,xt′∈τ(j)之间引入一条新边。 类似的,还要更新信息向量中所有对应于位姿
τ
j
\tau{j}
τj的值。这一操作的重要特点就是,它是局部的,只涉及到一小部分约束。当移除了所有到
m
j
m_j
mj的边之后,我们就可以安全的将
m
j
m_j
mj从信息矩阵和信息向量中移除。 得到的信息矩阵就更小了,因为它缺少了元素
m
j
m_j
mj。但是,该信息矩阵的后验概率在数学形式上,与移除
m
j
m_j
mj之前的后验概率等价。这个等价关系是符合直觉的, 我们用一系列直接与位姿节点相连的边替代了连接在
m
j
m_j
mj的边。这些边所构成的合力是一样的,只是
m
j
m_j
mj没有连接。
这一削减过程的优点就是,我们可以逐渐的将推理问题转换为一个更小的问题。通过解决
Ω
\Omega
Ω和
ξ
\xi
ξ中的每一个特征
m
j
m_j
mj, 最终我们会得到一个只定义在机器人路径上的更小的信息矩阵
Ω
~
\tilde{\Omega}
Ω~和信息向量
ξ
~
\tilde{\xi}
ξ~。这一约简过程可以以地图尺寸的线性时间进行,实际上它就是一种信息形式的消元求矩阵逆的方法, 在这种方法中我们还维护了一个信息状态。关于机器人路径的后验概率现在就可以写作
Σ
~
=
Ω
~
−
1
\tilde{\Sigma} = \tilde{\Omega}^{-1}
Σ~=Ω~−1和
μ
~
=
Σ
~
ξ
\tilde{μ} = \tilde{\Sigma}\xi
μ~=Σ~ξ。 不幸的是,我们的消元法并不能消除后验概率中的环,剩余的推理过程可能不止需要线性的时间。
最后一步,GraphSLAM算法恢复了特征的位置。概念上,就是对每一个
m
j
m_j
mj构建一个新的信息矩阵
Ω
j
\Omega_j
Ωj和信息向量
ξ
j
\xi_j
ξj。它们都是定义在特征
m
j
m_j
mj和观测到该特征的位姿集合
τ
(
j
)
\tau(j)
τ(j)上的。 它包含了
m
j
m_j
mj到
τ
(
j
)
\tau(j)
τ(j)之间的原始连接,以及取值为
μ
~
\tilde{μ}
μ~的没有不确定度的位姿
τ
(
j
)
\tau(j)
τ(j)。从这一信息形式中,使用通常的的矩阵求逆的方法,就可以很容易的计算出
m
j
m_j
mj的位置。 显然,
Ω
j
\Omega_j
Ωj只包含了那些关联在
m
j
m_j
mj上的元素,因此矩阵的逆运算可以以集合
τ
(
j
)
\tau(j)
τ(j)中位姿数量的线性时间来完成。
为什么图形的表达方式是如此自然的方式就很明显了。完全SLAM问题可以通过局部地将信息添加到一个大信息图中来解决,图中的每一条边对应着一次测量值
z
t
i
z_t^i
zti和控制量
u
t
u_t
ut。 为了将这些信息转换为地图和路径的估计,首先进行线性化,然后将位姿和特征之间的关系逐渐的转换为位姿对之间的关系。如此得到只约束了机器人位姿的结构,可以通过矩阵求逆解得。 一旦恢复了位姿,特征的位置就可以根据初始的特征位姿信息逐个解出。
2. GraphSLAM算法
下面我们将更精细准确的说明GraphSLAM算法的各个计算步骤。完全GraphSLAM算法fully GraphSLAM algorithm将被描述为几个步骤。实现的主要难度在于简单的增加信息的算法, 蕴含了将形式为
p
(
z
t
i
∣
x
t
,
m
)
p(z_t^i | x_t, m)
p(zti∣xt,m)和
p
(
x
t
∣
u
t
,
x
t
−
1
)
p(x_t | u_t, x_{t-1})
p(xt∣ut,xt−1)的条件概率转换为信息矩阵中的一个边。信息矩阵元素都是线性的,因此这一步也涉及到了线性化
p
(
z
t
i
∣
x
t
,
m
)
p(z_t^i | x_t, m)
p(zti∣xt,m)和
p
(
x
t
∣
u
t
,
x
t
−
1
)
p(x_t | u_t, x_{t-1})
p(xt∣ut,xt−1)。 在EKF SLAM中,线性化是通过计算在平均位姿
μ
0
:
t
μ_{0:t}
μ0:t处的雅可比矩阵得到的。为了构建我们的初始信息矩阵
Ω
\Omega
Ω和向量
ξ
\xi
ξ,我们需要一个对于所有位姿
x
0
:
t
x_{0:t}
x0:t的初始估计
μ
0
:
t
μ_{0:t}
μ0:t。
有很多种方法可以找到适用于线性化的初始均值
μ
μ
μ。比如说,我们可以运行一遍EKF SLAM算法并用它的估计值来进行线性化。本章中,我们将使用一种更简单的技术, 只是将运动模型
p
(
x
t
∣
u
t
,
x
t
−
1
)
p(x_t|u_t, x_{t-1})
p(xt∣ut,xt−1)简单地链接起来构成初始估计。该算法如图3.1所示,称为GraphSLAM_initialize。 该算法以控制量
u
1
:
t
u_{1:t}
u1:t为输入,输出是位姿估计序列
μ
0
:
t
μ_{0:t}
μ0:t。它将初始位姿定义为0,然后用速度运动模型依次估计后续位姿。因为我们只关注平均位姿向量
μ
0
:
t
μ_{0:t}
μ0:t, GraphSLAM_initialize只应用了运动模型中的确定性部分,而且也没有考虑任何测量值。

图3.1. GraphSLAM算法中初始化平均位姿向量
μ
1
:
t
μ_{1:t}
μ1:t。
一旦有了初始的估计
μ
0
:
t
μ_{0:t}
μ0:t,GraphSLAM算法就可以构建完全SLAM信息矩阵
Ω
\Omega
Ω和关联的信息向量
ξ
\xi
ξ。它是通过对图中的边线性化得到的, 图3.2中描述了GraphSLAM_linearize算法。

图3.2.GraphSLAM_linearize算法。
该算法中用到了很多数学符号,它们的意义将在后面推导该算法的时候得到明确。GraphSLAM_linearize以控制量
u
1
:
t
u_{1:t}
u1:t、测量值
z
1
:
t
z_{1:t}
z1:t、关联度变量
c
1
:
t
c_{1:t}
c1:t、 以及平均位姿估计
μ
0
:
t
μ_{0:t}
μ0:t做为输入,然后通过线性化操作逐渐的构建信息矩阵
Ω
\Omega
Ω和信息向量
ξ
\xi
ξ,不断地以子矩阵的形式添加每个测量值和控制量的信息。
具体来说, GraphSLAM_linearize 算法第2 行初始化了信息元素。 在第3行中,使用”无穷”信息元素将初始位姿
x
0
x_0
x0修正为
(
0
0
0
)
T
\begin{pmatrix} 0 & 0 & 0 \end{pmatrix}^T
(000)T。 这一过程是必须的,否则的话最后得到的矩阵可能是奇异的。这也说明一个事实,只通过相对信息我们是不能得到绝对估计的。
控制在GraphSLAM_linearize 算法的第4 -9 行被综合。 在其中的第5行和第6行中计算的位姿
x
^
\hat{x}
x^和雅可比矩阵
G
t
G_t
Gt是对非线性控制函数
g
g
g的线性化近似。 如这些公式所示,线性化过程所用的正是位姿估计
μ
0
:
t
−
1
μ_{0:t-1}
μ0:t−1其中
μ
0
=
(
0
0
0
)
T
μ_0 = \begin{pmatrix} 0 & 0 & 0 \end{pmatrix}^T
μ0=(000)T。这将导致第7行和第8行分别更新
Ω
\Omega
Ω和
ξ
\xi
ξ。 这些元素将分别添加到
Ω
\Omega
Ω和
ξ
\xi
ξ对应的行和列中。这一添加操作正是要将新的约束包含进SLAM的后验概率中,这正是上一节中讨论的算法思想的实践。
测量值是在GraphSLAM_linearize的第10到21行中整合的。 第11行中的矩阵
Q
t
Q_t
Qt正是我们所熟悉的测量噪声协方差。第13到17行,对测量函数进行了泰勒展开。 这里使用的是6.6节中定义的基于特征的模型。我们需要特别关注第16行的实现,因为角度的表达方式可以通过
2
π
2\pi
2π 转换。这一计算过程在第18和19行中进行测量更新时终止。在第18行中添加到
Ω
\Omega
Ω的矩阵尺寸是
6
×
6
6 × 6
6×6。我们将它分解为一个描述位姿
x
t
x_t
xt的
3
×
3
3×3
3×3的矩阵、一个描述特征
m
j
m_j
mj的
3
×
3
3×3
3×3的矩阵、 以及两个
3
×
3
3×3
3×3的矩阵用于描述
x
t
x_t
xt和
m
j
m_j
mj之间关系的矩阵。将之对应地添加到
Ω
\Omega
Ω的行和列中。类似的,添加到信息向量
ξ
\xi
ξ的向量的列维度是5。它被分为3维和2维的两个向量,并分别将它们添加到对应
x
t
x_t
xt和
m
j
m_j
mj的元素中。GraphSLAM_initialize的结果就是信息向量
ξ
\xi
ξ和矩阵
Ω
\Omega
Ω。我们已经注意到
Ω
\Omega
Ω是稀疏的,它只在主对角线、相邻位姿之间、位姿与地图特征之间对应的子矩阵处有非零值。 该算法的运行时间线性于获得数据的时间步数
t
t
t。

图3.3. GraphSLAM算法约简信息矩阵。
GraphSLAM算法的下一步就是消减信息矩阵和向量的维度。 它是通过图3.3中描述的GraphSLAM_reduce来实现的。 该算法以定义在整个地图特征和位姿空间下的
Ω
\Omega
Ω和
ξ
\xi
ξ做为算法的输入,输出是完全定义在位姿空间上的削减后的矩阵
Ω
~
\tilde{\Omega}
Ω~和向量
ε
~
\tilde{\varepsilon}
ε~, 需要注意该矩阵和向量与地图特征没有关系。削减过程通过GraphSLAM_reduce的第4到9行,逐个移除特征
m
j
m_j
mj来实现。记录
Ω
~
,
ξ
~
\tilde{\Omega}, \tilde{\xi}
Ω~,ξ~中每个元素的确切索引是很繁琐的, 因此图3.3中只提供了基本的思想。
第5行中计算了机器人观测到特征
j
j
j的位姿集合
τ
(
j
)
\tau(j)
τ(j)。接着从当前的
Ω
~
\tilde{\Omega}
Ω~中提取出两个子矩阵:
Ω
~
j
,
j
\tilde{\Omega}_{j,j}
Ω~j,j和
Ω
~
τ
(
j
)
,
j
\tilde{\Omega}_{\tau(j), j}
Ω~τ(j),j。
Ω
~
j
,
j
\tilde{\Omega}_{j,j}
Ω~j,j是
m
j
m_j
mj和
m
j
m_j
mj之间的二次子矩阵,
Ω
~
τ
(
j
)
,
j
\tilde{\Omega}_{\tau(j),j}
Ω~τ(j),j则是
m
j
m_j
mj与位姿变量
τ
(
j
)
\tau(j)
τ(j)之间的非对角元。它也从信息状态向量
ξ
~
\tilde{\xi}
ξ~中提取出对应于第
j
j
j个特征的元素,并标记为
ε
j
\varepsilon_j
εj。接着在第6行和7行中将其对应信息从
Ω
~
\tilde{\Omega}
Ω~和
ε
~
\tilde{\varepsilon}
ε~减去。在该操作之后,
m
j
m_j
mj所对应的行和列的元素都为0。接着就把这些行列移除,对应的削减了
Ω
~
\tilde{\Omega}
Ω~和
ξ
~
\tilde{\xi}
ξ~的维度。循环这一操作直到所有的特征都被移除了,
Ω
~
\tilde{\Omega}
Ω~和
ξ
~
\tilde{\xi}
ξ~中只保留了位姿变量。GraphSLAM_reduce算法的复杂度也是线性于时间步数
t
t
t 的。

图3.4. 更新后验概率
μ
μ
μ的算法。
GraphSLAM算法的最后一步就是计算机器人路径上所有位姿的均值和方差,以及地图中所有特征的平均位置估计。这是通过图3.4的GraphSLAM_solve来实现的。 第2行和第3行中计算路径估计
μ
0
:
t
μ_{0:t}
μ0:t,通过对约简的信息矩阵
Ω
~
\tilde{\Omega}
Ω~求逆,并将其结果与信息向量相乘。紧接着,GraphSLAM_solve在第4到第7行中依次计算每个特征的地址。 该算法返回的是机器人路径和所有地图特征的均值,以及机器人路径的协方差。我们注意到还有一种更高效的计算
μ
0
:
t
μ_{0:t}
μ0:t的方法,可以绕过对矩阵求逆。
GraphSLAM算法的解的质量依赖于GraphSLAM_initialize对初始均值估计的质量。这些估计的
x
x
x–
y
y
y要素,以一种线性的形式影响对应的模型,因此线性化并不依赖于这些值。 对于
μ
0
:
t
μ_{0:t}
μ0:t中的方向变量则不是这样。这些变量的初始化误差会影响泰勒近似的准确度,最终会影响到算法的结果。
为了降低线性化过程中以内泰勒近似而带来的误差,常会在同一个数据集上运行GraphSLAM_linearize, GraphSLAM_reduce, GraphSLAM_solve多次。 每次迭代都以上次迭代输出的均值向量
μ
0
:
t
μ_{0:t}
μ0:t作为输入,并输出一个新的,改进后的估计。只有当初始位姿估计具有很大偏差的时候,才需要对GraphSLAM进行迭代优化。通常迭代几次就可以得到比较好的结果了。

图3.5. 用于已知关联度的完全SLAM问题的GraphSLAM算法。
图3.5总结了最终的算法。它初始化了均值,然后就重复构造过程、约简过程、和求解过程。通常两三次迭代就能够收敛了,输出的均值
μ
μ
μ就是对机器人路径和地图的最好的估计。
四、RTAB-Map
更多关于RTAB-Map的使用将在之后的博客中展示。
更多信息请访问此处。

RTAB-Map(基于实时外观的映射)是一种基于增量基于外观的闭环检测器的RGB-D,基于立体声和激光雷达图的SLAM方法。闭环检测器使用词袋方法来确定新图像来自先前位置或新位置的可能性。当接受循环闭合假设时,新约束将添加到地图的图形中,然后图形优化器将地图中的错误最小化。使用内存管理方法来限制用于闭环检测和图形优化的位置数量,以便始终遵守对大型环境的实时约束。RTAB-Map可以与手持Kinect,立体相机或3D激光雷达一起单独使用以进行6DoF映射,也可以在配备有激光测距仪的机器人上进行3DoF映射。
RTAB-Map使用内存管理技术来限制在闭环检测期间被视为候选位置的位置数量。此技术是RTAB-Map的一项关键功能,它允许实时关闭循环。
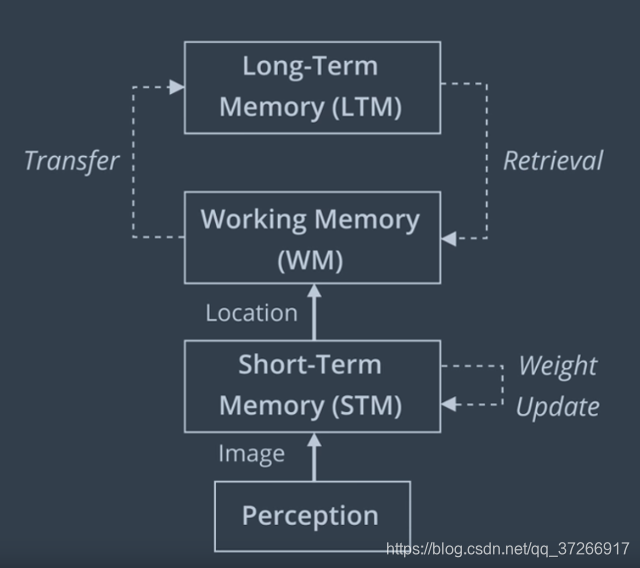
-
总体策略是将最新的和经常观察到的位置保留在机器人的工作内存(WM)中,并将其他位置转移到长期内存(LTM)中。
-
当获取新图像时,在短期存储器(STM)中创建一个新节点。
-
创建节点时,请记住提取特征并将其与词汇表进行比较,以找到图像中的所有单词,从而为此节点创建一个词袋。
-
在STM中,将根据机器人在该位置花费的时间为节点分配权重-时间越长,权重就越高。
-
STM具有固定的S大小。当STM到达S个节点时,最早的节点将移至WM以进行环路闭合检测。
-
循环关闭发生在WM中。
-
WM大小取决于固定的时间限制T。当处理新数据所需的时间达到T时,图形的某些节点从WM转移到LTM-结果,WM大小几乎保持恒定。
-
WM中最早的,权重较小的节点先转移到LTM,因此WM由较长时间的节点组成。
-
LTM不用于闭环检测和图形优化。
-
如果检测到环路关闭,则可以将旧节点的LTM中的邻居转移回WM(称为检索的过程)。