英文版教材第三章 1、2、3、4、6、7、9、11、14、15、16, 补充题1
-
一个上层分组(数据包)被分为 10 帧,每帧有 80%可能无损到达。如果在数据链路层没有差错控制,该报文要平均传送多少次才能正确交付?
考点:概率中的乘法和加法原理
答:整个报文无差错的到达接受端的概率
A
=
0.
8
10
=
0.107
A=0.8^{10}=0.107
A=0.810=0.107,因此成功发送1个报文平均需要传输的概率
=
1
0.107
=
9.3
=\frac{1}{0.107}=9.3
=0.1071=9.3
正规解法:假设第 k 帧发送成功,前面 k-1 帧全部失败,则平均传输次数=
Σ
k
=
0
∞
k
A
(
1
−
A
)
k
−
1
=
9.3
=\Sigma_{k=0}^{∞}kA(1-A)^{k-1}=9.3
=Σk=0∞kA(1−A)k−1=9.3
-
在一个数据流中有下列数据片段: A B ESC C ESC FLAG FLAG D,使用字节填充方法,填充之后的结果是什么?
考点:字节填充法
答:A B ESC ESC C ESC ESC ESC FLAG ESC FLAG D
-
试问字节填充算法的最大开销是多少?
考点:字节填充法中转义字符的处理
答:如果数据部分只有 FLAG 和 ESC 字符,则经过填充之后,原数据字符数和转义字符个数相同,因此开销 = 转义字符数/数据字符数 = 100%
-
使用位填充时,是否可能出现单比特差错(丢失、插入或者修改等),而通过校验和无法查出?如果不会,为什么?如果会,什么情况下会出现?校验和长度对此是否有影响?
考点:校验和概念和能力的理解
答:有可能。当使用位填充时,如果有单比特数据在传输的过程中发生改变,对于 n 位校验和,有
1
2
n
\frac{1}{2^n}
2n1 的概率无法查出错误,即被判断为校验和字段的 n 位数据的值恰好是使得对数据部分校验正确的值。校验和的位数越长,错误被忽略的概率越低。
-
为增强单比特校验的可靠性,一个差错检测编码使用一个校验位来检查所有奇数位,使用第二个校验位来检查所有偶数位。此编码的汉明距离是多少?
考点:海明距离的理解
答:增加了 2 位校验位后,编码的汉明距离是 2(数据中 1 个不同,则校验中 1 个不同)
-
假定利用海明码传送 16bit 报文,则需要添加多少 bit 的检查位才能确保接受方能够检测并纠正单个 bit 错误?如果传送 1101001100110101 的报文,在使用偶数校验方式,请给出传送的位模式。
考点:纠错码(海明码)
答:根据公式
m
+
r
+
1
≤
2
r
m+r+1≤2^r
m+r+1≤2r,当
m
=
16
m=16
m=16 时,r 最小为 5。因此需要添加 5bit 的检查位。

利用编码简便法有:码字中为1的位号为 b3, b5, b7, b11, b12, b15, b17, b19, b21,表示为二进制码并按模2求和,得到校验码P
5
P
4
P
3
P
2
P
1
=
01011
P_5P_4P_3P_2P_1=01011
P5P4P3P2P1=01011,因此发送的位模式为 111010110011001010101
-
一种检测差错的方法是把数据分成 n 行 k 列的数据块来传输,每行一个校验位,每列一个校验位,右下角的校验位对其所在行和列进行校验。这种方法可以检查出所有单比特差错吗?能检查出所有双比特差错吗?三比特差错呢?证明这种方法不能检查出某些四比特差错。
考点:行列同时校验方法的原理
答:可检查出所有单比特差错,一个单比特差错导致所在行列都出现校验错误。也可以检查出所有双比特差错,即使出错的两个比特在同行或者同列,也能查出。对于 3 比特差错, 如果在同行或同列,则该行或列的奇偶校验将检测出错误。 如果同行中有两个错误,则至少其中一个的列奇偶校验将检测到错误。 同列中有2个错误同理。对于 4 比特差错,如果出错的四个点正好位于矩形的 4 个顶点,则无法检查出差错。
-
假定数据以 1000 比特成块发送,可能发生 1 比特差错,出错的概率是独立的且重传不出错。误码率为多少时,采用奇偶校验检错并重传的方法要好于汉明码直接纠错?
考点:两种差错控制方法的理解及其开销的计算
答:若采用海明码直接纠错,根据不等式
m
+
r
+
1
≤
2
r
m+r+1 ≤ 2^r
m+r+1≤2r 可得到海明码校验位长度为 10,共需传输 1010 位;若采用奇偶校验并重传的方式,只需 1 位校验位,但需要计算重传开销。假设出错率为 p,采用检测重传的方式的开销
=
1001
+
1000
p
×
1001
<
1010
=1001+1000p×1001<1010
=1001+1000p×1001<1010,解得
p
<
8.99
×
1
0
−
6
p<8.99×10^{-6}
p<8.99×10−6
-
What is the remainder obtained by dividing
x
7
+
x
5
+
1
x^7 + x^5 + 1
x7+x5+1 by the generator polynomial
x
3
+
1
x^3 + 1
x3+1?
考点:检错码(CRC)
答:将M
(
x
)
=
x
7
+
x
5
+
1
M(x)=x^7 + x^5 + 1
M(x)=x7+x5+1 表示为2进制为 10100001,由题意知
r
=
3
r=3
r=3,将
M
(
x
)
M(x)
M(x) 左移 3 位得到:10100001000,
R
(
x
)
=
10100001000
%
G
(
x
)
=
111
R(x)=10100001000\%G(x)=111
R(x)=10100001000%G(x)=111
-
位流 10011101 使用教材中描述的标准 CRC 方法来进行校验。生成多项式是
x
3
+
1
x^3+1
x3+1。写出实际传输的位串。假定在传输中第三位被反转,证明在接收方能检测出差错。举例说明接收方不能检测出位差错的情形。
考点:CRC 校验原理的理解和计算
答:由生成多项式得到
r
=
3
r=3
r=3,因此将
M
(
x
)
M(x)
M(x) 左移 3 位得到 10011101000,将得到的结果
%
G
(
x
)
=
10011101000
%
1001
=
100
\%G(x)=10011101000\%1001=100
%G(x)=10011101000%1001=100,将 100 接在
M
(
x
)
M(x)
M(x) 后得到实际传输的位串 10011101100。
第三位被反转,则收到的位串为 10111101100,在接受端进行检错,将收到的位串%
G
(
x
)
=
10111101100
%
1001
=
100
≠
0
\%G(x)=10111101100\%1001=100≠0
%G(x)=10111101100%1001=100=0,则检测出错误。
当第 3 位和第 9 位同时发生反转时,即收到的位串为 10111101 000,此时校验的结果为 0,即接收方无法检测出错误。补充题1:已知数据位流为1101 0110,采用 CRC 校验,
G
(
x
)
=
x
3
+
1
G(x)=x^3+1
G(x)=x3+1,计算出校验位。
考点:CRC 校验的计算
答:由
G
(
x
)
G(x)
G(x) 可知
r
=
3
r=3
r=3,因此将数据左移 3 位得到 1001 0110 000,将得到的结果
%
G
(
x
)
=
10010110000
%
1001
=
111
\%G(x)=1001 0110000\%1001=111
%G(x)=10010110000%1001=111,得到的结果即为校验位 111。
英文版教材第三章17, 18, 20, 27, 28, 29, 30, 31, 32, 33,补充题2-5
-
在 3.3.3 节讨论的 ARQ 协议中,概述了一种情况:由于 ACK 帧丢失,对每一帧接收方都收到两次。如果数据帧和 ACK 都不丢失,接收方是否有可能收到重复的帧?
考点:ARQ 协议中出现重复帧情形的理解
答:有可能。例如某帧正确到达,但接收方因为 CPU 忙、处理速度慢等原因而推迟了 ACK 的发送,导致发送方的定时器超时,重发数据帧。此时,接收方将收到重复帧。
注意:出错帧不算重复帧
-
某信道的数据率是 4 kbps,传播时延是 20 毫秒,帧长为多少时,停等协议的效率能至少能达到 50%?
考点:停等协议的信道利用率
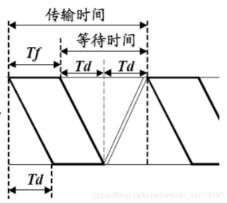
答:由题意知:T
f
=
L
4
k
b
p
s
,
T
d
=
20
m
s
T_f=\frac{L}{4kbps},T_d=20ms
Tf=4kbpsL,Td=20ms,信道利用率
C
r
=
T
f
T
f
+
2
T
d
≥
50
%
Cr=\frac{T_f}{T_f+2T_d}≥50\%
Cr=Tf+2TdTf≥50%,代入得
L
≥
160
b
i
t
L≥160bit
L≥160bit
-
一条 3000 公里长的 T1 中继线路使用协议 5 来传输 64 字节长的数据帧。如果传播速度为 6 微妙/公里,需要多少位序列号?
考点:对于 Gobackn 协议性能的理解和计算;T1 的发送速率
答:假定序号为 n 位,Gobackn 协议的最大发送窗口
W
S
=
2
n
−
1
W_S=2^n-1
WS=2n−1,应使信道利用率
C
r
=
W
S
×
T
f
T
f
+
2
T
d
=
100
%
Cr=\frac{W_S×T_f}{T_f+2T_d}=100\%
Cr=Tf+2TdWS×Tf=100%。
传播时延T
d
=
3000
×
6
=
18
m
s
T_d=3000×6=18ms
Td=3000×6=18ms,发送时延
T
f
=
64
×
8
/
1.536
M
b
p
s
=
0.3
m
s
T_f= 64×8/1.536Mbps = 0.3ms
Tf=64×8/1.536Mbps=0.3ms,代入上式求得
W
S
≥
121
W_S≥121
WS≥121,则对应的
n
≥
7
n≥7
n≥7,需要 7 位序号。
总结:滑动窗口协议不会发生序号回转问题,当题目要求计算序号位数时,只考虑信道利用率。
-
在带宽为 1Mbps 的无差错链路上使用协议 6 进行通信,设最大帧长为 1000 位,网络层每秒产生一个新的数据包,重传超时间隔为 10ms。如果不使用 ACK 定时器,将产生不必要的重传。求一帧的平均重传次数。
考点:选择重传协议的工作原理和流程
答:确定是否会发生超时:传输时间
=
1000
b
1
M
b
p
s
=
1
m
s
=\frac{1000 b}{1Mbps}=1ms
=1Mbps1000b=1ms,而
10
+
1
m
s
≪
1
s
10+1ms≪1s
10+1ms≪1s,所以超时不可避免;
确定是否会产生 NAK 帧:超时后发送端会重发帧,接收端发现重复,回 NAK,然后发送端可发新帧(序号滚动)。
因此,平均每帧传送2次。 -
协议 6 中,MAX_SEQ
=
2
n
−
1
=2^n − 1
=2n−1. 很明显这个条件有利于帧头字段的有效使用,但我们没有说明这个条件是必须的。对于 MAX_SEQ = 4,协议是否能正确工作?请举例说明。
考点:MAX_SEQ 和
arrived[]在协议6中的作用,与模运算的关系;情景假设答:若 MAX_SEQ=4,则模
=
5
,
W
s
=
W
r
=
5
2
=
2
=5, Ws=Wr=\frac{5}{2}=2
=5,Ws=Wr=25=2,则只有两个缓冲区
in_buf[0]和in_buf[1],序号从0-4开始轮回,0,2,4使用in_buf[0],1,3使用in_buf[1]。假设0,1,2,3都正确收到并已回复ACK,则下一步发送4,0。若4丢失但0成功接收时,0号帧会占用in_buf[0],此时arrive[0]=true,则while中的数据发生错序上交。 -
在 1Mbps 的卫星信道上发送多个长度为 1000 位的帧。从地面到卫星的传播时延是 270 毫秒,采用捎带确认(piggybacking)方式。帧头很短,且使用 3 位序号。请分别计算采用下列协议的最大信道利用率:
(a) 停等协议
(b) 协议 5
(c ) 协议 6考点:信道利用率的计算(单个信道),一定画出时序图:
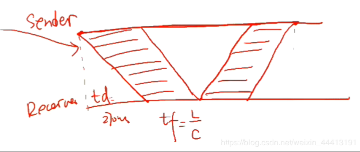
答:因为总是使用捎带应答技术,因此信道利用率C
r
=
T
f
2
T
f
+
2
T
d
Cr=\frac{T_f}{2T_f+2T_d}
Cr=2Tf+2TdTf,信道传播时延
t
传
=
1
k
1
M
b
p
s
=
1
m
s
t_传=\frac{1k}{1Mbps}=1ms
t传=1Mbps1k=1ms
(a)C
r
=
1
2
×
1
+
2
×
270
=
0.185
%
Cr=\frac{1}{2×1+2×270}=0.185\%
Cr=2×1+2×2701=0.185%。
(b)W
s
=
2
3
−
1
=
7
Ws=2^3-1=7
Ws=23−1=7,则
C
r
=
1
×
7
2
×
1
+
2
×
270
=
1.29
%
Cr=\frac{1×7}{2×1+2×270}=1.29\%
Cr=2×1+2×2701×7=1.29%
(c)W
s
=
2
3
−
1
=
4
Ws=2^{3-1}=4
Ws=23−1=4,则
C
r
=
1
×
4
2
×
1
+
2
×
270
=
0.738
%
Cr=\frac{1×4}{2×1+2×270}=0.738\%
Cr=2×1+2×2701×4=0.738%
其他同类考题:
W
s
Ws
Ws为多少时效率能达到100%?
W
s
>
W
s
m
a
x
Ws>Ws_{max}
Ws>Wsmax 时效率为多少(还是100%)?
-
在 64kbps 的无差错卫星信道上单方向发送多个长度为 512 字节的数据帧,反向会送较短的 ACK 帧。地面-卫星的传播时延是 270 毫秒。当发送窗口分别为 1、7、15、127 时,最大吞吐量各是多少?
考点:极限信道利用率与吞吐量的计算
答:512 字节数据帧发送时延
=
512
×
8
b
i
t
64
k
b
p
s
=
64
m
s
=\frac{512×8bit}{64kbps}=64ms
=64kbps512×8bit=64ms。接受端回一个很短的 ack(不计发送时间),因此时序图如下:
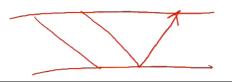
信道利用率达到 100% 时有W
S
⋅
T
f
≥
2
T
d
+
T
f
W_S·T_f≥2T_d+T_f
WS⋅Tf≥2Td+Tf,所以在
W
S
≥
9.4375
W_S≥9.4375
WS≥9.4375,即
W
S
>
10
W_S>10
WS>10 时,吞吐量
=
64
k
b
p
s
=64kbps
=64kbps。当窗口大小
=
n
(
n
≤
9
)
=n(n≤9)
=n(n≤9) 时,吞吐率
=
64
n
64
+
2
×
270
=\frac{64n}{64+2×270}
=64+2×27064n。当
n
=
1
,
7
,
15
,
127
n=1,7,15,127
n=1,7,15,127 时代入上式,得到结果为(吞吐量=吞吐率×带宽):
| 窗口大小
W W W |
1 | 7 | 15 | 127 |
|---|---|---|---|---|
| 吞吐量 | 6.78kbps | 47.5kbps | 64kbps | 64kbps |
-
在一条 100 公里长的电缆上采用 T1 速率来发送数据,电缆的传播时延是真空中光速的 2/3。请问多少位数据可以充满电缆?
考点:时延带宽积的计算
答:电缆的传输速率
=
2
3
×
3
×
1
0
8
=
2
×
1
0
8
m
/
s
=\frac{2}{3}×3×10^8=2×10^8 m/s
=32×3×108=2×108m/s,则传播时延
=
100
k
m
2
×
1
0
8
m
/
s
=
5
×
1
0
−
4
s
=\frac{100km}{2×10^8 m/s}=5×10^{-4} s
=2×108m/s100km=5×10−4s,T1的带宽
=
1.544
M
b
p
s
=1.544Mbps
=1.544Mbps,则电缆中容纳的比特(时延带宽积)
=
5
×
1
0
−
4
×
1.544
M
b
p
s
=
772
b
i
t
=5×10^{-4}×1.544Mbps=772bit
=5×10−4×1.544Mbps=772bit
-
为什么 PPP 使用字节填充而不使用位填充?请写出至少一个原因。
考点:PPP的特点
答:①PPP是由软件实现的,而位填充在硬件协议中实现,对于软件实现,字节操作比位操作更简单;②PPP是设计用于调制解调器的,调制解调器接收和传送数据的单位是字符而不是位。
-
在 PPP 帧中承载 IP 数据包的最小开销是多少?只计算 PPP 本身的开销,不考虑 IP 包头。最大开销是多少?
考点:PPP帧的数据结构
答:最小开销是:每帧有2个标志字节、1个协议字节和2个校验字节,每帧总共5字节开销;
最大开销是:2个标志字节、1个地址字节、1个控制字节、2个协议字节和4个校验字节,一共10字节开销。补充题:The following character encoding is used in a data link protocol:
A: 01000111 B: 11100011 FLAG: 01111110 ESC: 11100000
Show the bit sequence transmitted (in binary) for the four-character frame A B ESC FLAG when each of the following framing methods is used:
(a) Byte count.
(b) Flag bytes with byte stuffing.
(c ) Starting and ending flag bytes with bit stuffing.考点:3种成帧方式
答:(a)00000100 01000111 11100011 11100000 01111110(4 A B ESC FLAG)
(b)01111110 01000111 11100011 11100000 11100000 11100000 01111110 01111110(FLAG A B ESC ESC ESC FLAG FLAG)
(c)01111110 01000111 110100011 111000000 011111010 (A B ESC FLAG)
注意:考试经常反向考(给HDLC帧,还原数据) -
Data link protocols almost always put the CRC in a trailer rather than in a header. Why?
考点:计算机网络的串行通信
答:串行通信,接受完帧后可直接看校验位,节省存储,加速;否则要额外存储 CRC,效率降低
-
如果Go back N 中的between函数检查的条件是
a
≤
b
≤
c
a≤b≤c
a≤b≤c 而不是
a
≤
b
<
c
a≤b<c
a≤b<c,则对于协议的正确性和效率有影响吗?
考点:理解GBN的流程和原理;假设场景,利用错误样例来推翻题目中的假设
答:有影响。 考虑以下情况(3bit举例):先发送7号帧,成功接收并返回ACK;接着连发0-6号帧,但发生丢失。接收端等不到 ACK,触发timeout事件,重新发送刚才的帧,此时携带的 ACK=7。发送端检测到7满足
a
≤
b
≤
c
a≤b≤c
a≤b≤c,误认为 0-6 号帧成功发送。在未收到0-6号帧时,发送端未进行回退,导致帧顺序出错。
-
在一个负载很重的 50Kbps 的卫星信道上使用协议6,数据帧包含 40bit 的头和 3960bit 的数据,请计算一下浪费在头部和重传的开销占多少比例?
假设从地球到卫星的信号传输时间为270ms。
ACK 帧永远不会发生;
NAK 帧为40bit。
数据帧的错误率为1%,NAK帧的错误率忽略不计。
序号位为8位。
考点:根据已知条件和协议分析,画出时序图
答:帧长度=
40
+
3960
=
4000
b
i
t
=40+3960=4000bit
=40+3960=4000bit,发送时延
=
4000
50
k
b
p
s
=
80
m
s
=\frac{4000}{50kbps}=80ms
=50kbps4000=80ms,因为未发送 ack,则一定采用了捎带应答技术,由此画出时序图:
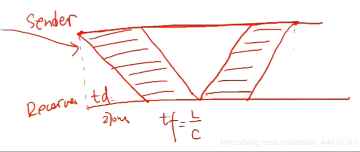
成功发送一帧的时间=
2
×
80
+
2
×
270
=
700
m
s
=2×80+2×270=700ms
=2×80+2×270=700ms.已知序号位为8位,则
W
s
=
2
n
−
1
=
2
7
=
128
Ws=2^{n-1}=2^7=128
Ws=2n−1=27=128,对应的发送时延
=
128
×
80
=
10240
m
s
>
>
700
m
s
=128×80=10240ms>>700ms
=128×80=10240ms>>700ms,则此时的链路利用率是100%,管道中充满了比特。
每个帧重传开销=
4000
×
1
%
=
40
b
i
t
=4000×1\%=40bit
=4000×1%=40bit
每个帧 nak 开销=
40
×
1
%
=
0.4
b
i
t
s
=40×1\%=0.4bits
=40×1%=0.4bits
协议头40bit,因此总的开销=
40
+
0.4
+
40
=
80.4
b
i
t
=40+0.4+40=80.4bit
=40+0.4+40=80.4bit,所占比例
=
80.4
80.4
+
3960
=
1.99
%
=\frac{80.4}{80.4+3960}=1.99\%
=80.4+396080.4=1.99%
补充题1:一个PPP帧的数据部分(用十六进制写出)是7D 5E FE 27 7D 5D 7D 5D 65 7D 5E。试问真正的数据是什么(用十六进制写出)?
考点:字节填充的理解
答:由于PPP的字节填充法规定:
0x7E转换为(0x7D, 0x5E);0x7D转换为(0x7D, 0x5D)

补充题2:在网络中截获了一串数据,用十六进制表示为:06 7E 25 7D 5E 16 7D 5D 7E A8 FF,其中包含一个完整的PPP帧,请以十六进制写出该PPP帧的内容(不包含首尾标志)
考点:对字节填充首尾标志法的理解
答:PPP帧的帧头、帧尾都是 7E,因此完整的传输帧是 7E 25 7D 5E 16 7D 5D 7E,去掉帧头帧尾和填充字节,帧中的内容是:25 7E 16 7D补充题3. 采用 3 比特序号的选择重传(SR)协议,若接收窗口为5,则发送窗口的最大值是多少?
考点:选择重传协议中发送窗口和接收窗口的个数之间关系
答:使用 n 位序号的选择重传协议的滑动窗口个数应满足
W
S
+
W
R
≤
2
n
W_S+W_R≤2^n
WS+WR≤2n,对于 3 位序号,
W
S
+
W
R
≤
8
,
W
R
=
5
W_S+W_R≤8,W_R=5
WS+WR≤8,WR=5,则
W
S
≤
3
W_S≤3
WS≤3
补充题4. 50-kbps 的卫星信道,往返时延为 500ms,帧长为 1000 位,使用捎带确认(搭载ACK)的SR协议,若使效率达到50%,序号的比特数至少是多少?
补充题5. 数据链路层采用GBN(回退N步) 协议,发送方已经发送了编号为0-7 的帧,当计时器超时时,若发送方只收到0、4、5 号帧的确认,则发送方需要重发的帧数是多少?
考点:累积确认
答:对 5 号帧的确认说明 5 号帧及以前的帧全部正确接收,因此发送方需要重发未确认的 6 号和 7 号帧,即需要重发的帧数是 2。
补充题6. 两台计算机的数据链路层协议实体采取滑动窗口机制利用16kbps 的卫星信道传输长度为128 字节的数据帧,信道传播时延为270ms。
(1) 计算使用停等协议的信道利用率;
(2) 计算使用发送窗口为7 的GBN 协议的信道利用率;
(3) 计算使用发送窗口为15 的GBN 协议的信道利用率;
(4) 为使信道利用率达到最高,使用GBN 协议时序号的比特数最少为多少位?