一、矩阵的产生

首先引入例题

这个题显然是线性规划的问题，有初始变量和约束条件，求S的最优化。

 

编程方式一：

暴力枚举

如图：

得到结果：

结果如何看呢？

重要的部分只有这么几点：

1、运行时间

2、Objective value：

编程方式二：

定义集合段

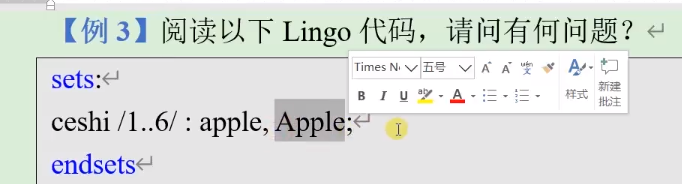
带括号表示是矩阵，可以看到我们在set段定义了一些矩阵a,b,x,y；factory代表1到6的称呼。

以上两句话是一个意思，没有必要写那么麻烦，按照解的内容写即可。

 

二、矩阵的赋值

sets:
fatory /1..6/:a,b;
plant/1..3/:x,y;
endsets

data:
a = 1,2,3,4,5,6;
b = 6 5 4 5 3 1;
x =  10 20 30;
enddata

注意一下语法，不要多赋值和少赋值！

sets:

endsets

data

enddata

注意

1、有的矩阵是被求的矩阵，不需要赋值；

2、赋值不能赋值分数；

可以多试会不会报错，要享受报错的过程，这样以后就会怎么不会报错了~~~

三、循环与求和

这一节比较重要

题目中的可以用for循环写出来

@for( gc(i):a(i)*x(i) = s );

max = s;!目标函数;
@for( gc(i):a(i)*x(i) = s );
!for循环要括起整行的语句，比如s不能在外面，这是因为
这句话本质上是循环了刚才暴力写的S=a1*x1直到S=a5*x5；
！for循环的内部呢，一定要先写gc（集合定义的名称）因为gc是定义为
1行5列的矩阵，我们要告诉后面的i是循环了5次（i接在矩阵后面）。
!此处的i可有也可没有，也可以换成j,k,m;
!二维矩阵工厂出现后同时出现i,j就必须带i,j了
以上不太懂没有关系照着先写就行，这只是语法的问题。;

@sum(gc(i):x(i))=5000;

!注意这个5000在外面，因为sum只是x(1)+x(2)+..=5000

 

四、二维矩阵

cooper(gc,plant) : e,f;为5*8的二维矩阵；

例题:

title:example;


sets:
factory /1..6/:a;
plant /1..8/:d;
cooper(factory,plant):c,x;
endsets

data:
a = 60 55 51 43 41 52;
d = 35 37 22 32 41 32 43 38;
c = 6 2 6 7 4 2 5 8
    4 9 5 3 8 5 8 2
    5 2 1 9 7 4 3 3
    7 6 7 3 9 2 7 1
    2 3 9 5 7 2 6 5
    5 5 2 2 8 1 4 3;
enddata

min = @sum(cooper(i,j):c(i,j)*x(i,j));
@for(factory(i):@sum(plant(j):x(i,j))<=a(i));
!注意sum求和只是x(i,j)这个，不要把a(i,j)也套进去。
sum求和的起止位置很重要。;
@for(plant(i):@sum(factory(j):x(j,i)) = d(i));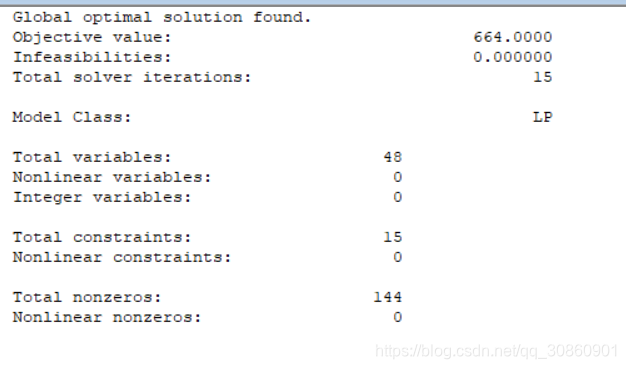

鸣谢;

https://www.bilibili.com/video/BV1Ui4y1G7rV?from=search&seid=7530803033979932620