贾俊平《统计学基于R》（第三版）第八章方差分析习题答案

前言

本文习题基于R语言，主要探讨R语言对于方差分析的运用，建议学习统计学的朋友，还是手动计算+查表求得答案，毕竟以后很少再会手算了。

课后习题答案，答案来自本人自做，如有错误欢迎联系我更正，先谢了。为方便大家处理数据，所有数据都已经手动录入，不需要载入任何csv或者其他文件。

提示：以下是本篇文章正文内容，下面案例可供参考

一、什么是方差分析？

方差分析，英文 analysis of variance，AN O VA，组合起来就叫做ANOVA，顾英文名思义，就是分析差异的一种分析。
方差分析分析的是类别变量对数值变量的影响，所以如果是单因子方差分析的话，就需要一个data.frame，一列是所有类别类型，另一列是类别类型对应的数值。通常这类数据都是宽表，我们需要做一些变换，将数据格式转化为长表，然后就可以开始分析了。

方差分析函数aov(数值变量名~类别变量名，dataframe名）

二、用到的R函数

1.data.frame数据框
2.aov()函数
3.kuskal.test
4.ks.test
5.shapiro.test
6.LSD,HSD
7.常用用于分析模型的summary函数
8.melt函数，用于宽表转化为长表

三、课后习题答案

习题8.1

#贾俊平-统计学基于R，第八章，练习题8.1
df8.1<-data.frame(c(4.05,4.01,4.02,4.04,4.00,4.03),c(3.99,4.02,4.01,3.99,4.00,4.05),c(3.97,3.98,
              3.97,3.95,4.02,4.00),c(4.00,4.02,3.99,4.01,4.00,4.03))
colnames(df8.1)<-c('机器1','机器2','机器3','机器4');df8.1
library(reshape2)
a <- melt(df8.1);a
colnames(a)=c('机器','value')
attach(a)
mode1<-aov(value~机器)

mode1$coefficients
mode1$fitted.values
summary(mode1)

#输出以下：
# Df   Sum Sq   Mean Sq F value Pr(>F)  
# 机器         3 0.005846 0.0019486   4.576 0.0135 *
#   Residuals   20 0.008517 0.0004258                 
# ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

#由于问题是在0.01上是否显著，由于p值0.0135>0.01所有接受原假设，（原假设是没有差异）
#所以结论是机器对装填量没有显著影响。（如果是0.05那就有显著影响了）



library(agricolae)
lsdmode<-LSD.test(mode1,'机器')
lsdmode#通过group分组，不同字母间有显著差异，相同字母没有显著差异


library(DescTools)
PostHocTest(mode1,method = 'lsd')#通过两辆比较，p值很小说明有显著差异
# Posthoc multiple comparisons of means : Fisher LSD 
# 95% family-wise confidence level

# $机器
# diff       lwr.ci       upr.ci   pval    
# 机器2-机器1 -0.015000000 -0.039852260  0.009852260 0.2225    
# 机器3-机器1 -0.043333333 -0.068185594 -0.018481073 0.0016 ** 
# 机器4-机器1 -0.016666667 -0.041518927  0.008185594 0.1772    
# 机器3-机器2 -0.028333333 -0.053185594 -0.003481073 0.0275 *  
# 机器4-机器2 -0.001666667 -0.026518927  0.023185594 0.8901    
# 机器4-机器3  0.026666667  0.001814406  0.051518927 0.0367 *  
#   
#   ---
#   Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

library(agricolae)
HSD <- HSD.test(mode1,'机器');HSD
hsdtukey<-TukeyHSD(mode1)
plot(hsdtukey)
#效应量计算
EtaSq(mode1,anova = T)#eta.sq值0.407，即为效应量

ks.test(a$value,'pnorm',mean(a$value),sd(a$value))#ks.test正态性检验，参数比较多
shapiro.test(a$value)#shapiro.test参数比较少，都是检验正态性
qqnorm(jitter(a$value))
qqline(jitter(a$value))
plot(density(a$value))#符合正态性分布
#检查方差齐性：
bartlett.test(value~机器,data=a)#原假设，方差齐，p值0.7073,接受原假设，说明方差齐

习题8.2

#贾俊平-统计学基于R，第八章，练习题8.2

df8.2<-data.frame(c(7,7,8,7,9,8),c(8,9,8,10,9,10),c(5,6,5,7,4,8));df8.2
colnames(df8.2)<-c('High','Middle','Base')
df8.2
library(reshape2)
a8.2<-melt(df8.2)
colnames(a8.2)<-c('levels','score')
a8.2
mode8.2<-aov(score~levels,data = a8.2)
summary(mode8.2)

#LSD
library(agricolae)
lsd8.2<-LSD.test(mode8.2,'levels')
lsd8.2
library(Desctools)
PostHocTest(mode8.2,method = 'lsd')#通过两辆比较，p值很小说明有显著差异

#HSD

library(agricolae)
HSD <- HSD.test(mode8.2,'levels');HSD
hsdtukey8.2<-TukeyHSD(mode8.2)
plot(hsdtukey)
#效应量计算
EtaSq(mode8.2,anova = T)#eta.sq值0.625，即为效应量

#8.2第三小题
shapiro.test(a8.2$score)
qqnorm(jitter(a8.2$score));qqline(jitter(a8.2$score))
plot(density(a8.2$score))
skewness(a8.2$score)

ks.test(a8.2$score,'pnorm',mean=mean(a8.2$score),sd=sd(a8.2$score))
#8.2第四小题
kruskal.test(a8.2$score~a8.2$levels)# p-value = 0.004623，拒绝相同的假设，有明显差异
#说明高层与底层的看法还是有明显不同的，你懂的，格局

习题8.3

#习题8.3
df8.3 <- data.frame(c(50,50,43,40,39),c(32,28,30,34,26),c(45,42,38,48,40))
colnames(df8.3)<- c('A',"B","C")
df8.3
a8.3<-melt(df8.3)
colnames(a8.3) <- c('company','time')
head(a8.3)
mode8.3<-aov(time~company,a8.3)
summary(mode8.3)#pvalue 0.00031 表明企业之间有显著差异

EtaSq(mode8.3,anova = T)#eta.sq值0.7399，即为效应量


HSD8.3 <- HSD.test(mode8.3,'company');HSD8.3
hsdtukey8.3<-TukeyHSD(mode8.3);hsdtukey8.3
plot(hsdtukey8.3)

习题8.4

#习题8.4
seedandfert<-data.frame(c('seed1','seed2','seed3','seed4','seed5'),c(12.0,13.7,14.3,14.2,13.0),
                        c(9.5,11.5,12.3,14.0,14.0),c(10.4,12.4,11.4,12.5,13.1),
                        c(9.7,9.6,11.1,12.0,11.4))
colnames(seedandfert)<-c('kind','fert1','fert2','fert3','fert4')
seedandfert
library(reshape2)
?melt
seedandfertlong<-melt(seedandfert,id.vars = 'kind')
colnames(seedandfertlong)<-c('seedkind','fertkind','value')#也可以用rename函数
head(seedandfertlong)
mode8.4<-aov(value~seedkind+fertkind,data = seedandfertlong)
summary(mode8.4)
# Df Sum Sq Mean Sq F value  Pr(>F)   
# seedkind     4 19.067   4.767   7.240 0.00332 **
#   fertkind     3 18.181   6.060   9.205 0.00195 **
#   Residuals   12  7.901   0.658                   
# ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#说明肥料和种子品种都对发芽有影响

#8.4第二小题
library(DescTools)
EtaSq(mode8.4)#两个效应量都是0.4多，说明还是有影响的
#输出结果：
# eta.sq eta.sq.part
# seedkind 0.4223081   0.7070231
# fertkind 0.4026955   0.6970766

习题8.5

#以下是统计学基于R第八章第五题练习题的解答

traffic<-data.frame(c('HighTraffic','HighTraffic','HighTraffic','HighTraffic','HighTraffic',
                      'LowTraffic','LowTraffic','LowTraffic','LowTraffic','LowTraffic'),
                    c(36.5,34.1,37.2,35.6,38.0,30.6,27.9,32.4,31.8,27.3),
                    c(28.1,29.9,32.2,31.5,30.1,27.6,24.3,22.0,25.4,21.7),
                    c(32.4,33.0,36.2,35.5,35.1,31.8,28.0,26.7,29.3,25.6))
colnames(traffic)<-c('Time','Road1','Road2','Road3');traffic

#library(reshape2)#加载reshape2 或者reshape包，这里上面已经加载过，你需要加载
trafficlong<-melt(traffic,id.vars = 'Time')#从宽表（二维）转化为长表（一维）
colnames(trafficlong)<-c('Time','Road','value')
head(trafficlong)

mode8.5<-aov(value~Time+Road+Time:Road,data = trafficlong)
summary(mode8.5)
mode8.5$coefficients

# (Intercept)           TimeLowTraffic                RoadRoad2 
# 36.28                    -6.28                    -5.92 
# RoadRoad3 TimeLowTraffic:RoadRoad2 TimeLowTraffic:RoadRoad3 
# -1.84                     0.12                     0.12 


EtaSq(mode8.5)

# eta.sq  eta.sq.part
# Time      5.082696e-01 0.7455777387
# Road      3.182453e-01 0.6472503358
# Time:Road 4.231172e-05 0.0002438925

#从数据中我们得出结论，
#1、堵车和时段有关系，堵的时候都堵
#2、堵车和路段有关系，热门的路肯定更堵
#3.没有明显的迹象表明，路段和时间之间有相互作用，只有非高峰期路段2路段3降低的非常明显

习题8.6

#习题8.6答案
advertisement<-data.frame(c('A','A','B','B',"C",'C'),
                          c(8,12,22,14,10,18),
                          c(12,8,26,30,18,14))
colnames(advertisement)<-c('Plan','报纸','电视')
advertisement
library(reshape2)
adv<-melt(advertisement,id.vars = 'Plan')
colnames(adv)<-c('Plan','Channel','Result')
mode8.6<-aov(Result~Plan+Channel,data = adv)
summary(mode8.6)
mode8.6$coefficients


mode8.62<-aov(Result~Plan+Channel+Plan:Channel,data = adv)
mode8.62$coefficients
summary(mode8.62)


library(DescTools)
EtaSq(mode8.62)
# 
# eta.sq eta.sq.part
# Plan         0.63235294   0.7818182
# Channel      0.08823529   0.3333333
# Plan:Channel 0.10294118   0.3684211
#结果显示广告效果与方案（Plan）最有关系，渠道，渠道与方案的互相作用对广告效果的影响都有限

小结

方差分析主要研究的是类型变量对于数值的影响，把握这个基本点，我们在做分析以及拿到数据做处理的时候，就都应该朝着这个方向去做。

值得注意的是，按道理来讲做所有方差分析之前都要检验数据正态性，方差齐性，以及数据独立性（数据独立性研究者在设计获取数据来源的时候可以设置，所以无需检测），如果不满足条件只能条用非参方法kruscal.test.文末放上我对于本章学习的一个小结的思维导图

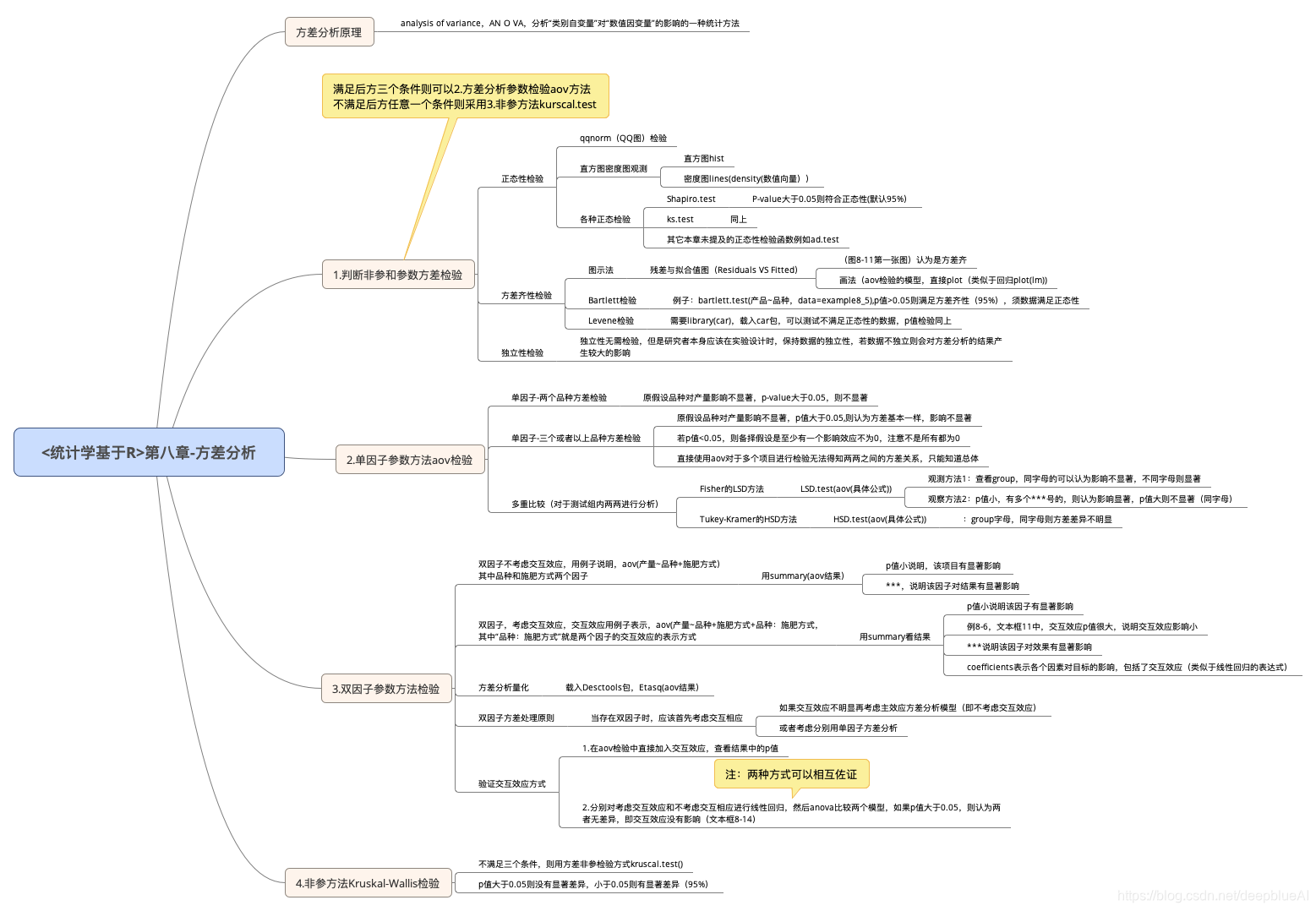
方差分析章节思维导图