实验1 线性表

1、用 SqList 类型自行建立两个有序的顺序表，然后将其合并成一个新的有序表（即实现算法2.7）。

#include <stdio.h>
#include <stdlib.h>
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
#define OK 1
#define OVERFLOW 0
#define ERROR 0
//目标： 顺序表的合并
typedef struct{
    int *elem; //数据元素
    int length; //元素长度
    int listsize; //存储空间大小
} SqList;

//初始化顺序表L
int InitList_Sq(SqList* L){
    L->elem = (int*)malloc(LIST_INIT_SIZE * sizeof(int));
    if( !L->elem )exit( OVERFLOW );
    L->length = 0; //元素长度为 0
    L->listsize = LIST_INIT_SIZE; //分配初始存储空间
    return OK;
}

//获取表中第 i 个位置元素，储存到 e
//void GetElem(SqList L, int i, int *e){
//    *e = *(L.elem + i - 1);
//}

//获取表中元素长度
int ListLength(SqList L){
    return L.length;
}

//扩容表的存储容量，每次增加 10 个数据的容量
void ListExpand(SqList* L){
    int* newbase = (int*)malloc((L->listsize + LISTINCREMENT)*sizeof(int));
    L->elem = newbase;
    L->listsize += LISTINCREMENT;
}

//在表L中第 i 个位置插入新的元素 e ，L元素长度加 1
void ListInsert(SqList* L, int i, int e){
    *(L->elem + i - 1) = e;
    L->length++;
}

//判断输入的数据是否非递减
void DataJudge(SqList L){
    for(int m=0; m<L.length-1; m++){
        if(L.elem[m] > L.elem[m+1]){
            printf("输入数据有误，请核对后按非递减顺序输入。\n");
            exit(ERROR);
        }
    }
}

//合并两个顺序表
void MergeList_Sq(SqList La, SqList Lb, SqList *Lc){
    //具体可实现：
    //已知的顺序表La，Lb中，元素按非递减顺序排列
    //归并La和Lb至Lc中，Lc仍然按非递减顺序排列
    int *pa = La.elem, *pb = Lb.elem; //定义两个操作指针
    
    Lc->listsize = Lc->length = ListLength(La) + ListLength(Lb); //Lc元素长度、储存空间赋值
    int *pc = Lc->elem = (int*)malloc(Lc->listsize * sizeof(int));//Lc操作指针
    if( !Lc->elem )exit(OVERFLOW); //内存分配失败
    
    int *pa_last = La.elem + ListLength(La) - 1; //顺序表末地址
    int *pb_last = Lb.elem + ListLength(Lb) - 1;
    
    //合并
    while(pa<=pa_last && pb<=pb_last){
        if(*pa <= *pb) *pc++ = *pa++;
        else *pc++ = *pb++;
    }
    while(pa <= pa_last) *pc++ = *pa++;
    while(pb <= pb_last) *pc++ = *pb++;
}

//输出合并后的顺序表
void PrintMergedList_Sq(SqList* Lc){
    printf("合并后的顺序表元素依次为：");
    for(int m=0; m<Lc->length; m++){
        printf("%d ", Lc->elem[m]);
    }
    printf("\n");
}

int main() {
    SqList La, Lb, Lc;
    
    InitList_Sq(&La);
    InitList_Sq(&Lb);
    InitList_Sq(&Lc);
    
    int len_a = 0, len_b = 0;
    printf("请分别输入顺序表La、Lb的元素长度，以空格键分开：\n");
    scanf("%d %d", &len_a, &len_b);
    
    if(len_a > La.listsize){ //输入元素长度是否溢出
        do{
            ListExpand(&La);
        }while(La.listsize >= len_a);
    }
    if(len_b > Lb.listsize){ //输入元素长度是否溢出
        do{
            ListExpand(&Lb);
        }while(Lb.listsize >= len_b);
    }
    
    int i = 0, e1 = 0;
    printf("请输入顺序表 La 的各元素(非递减顺序):\n");
    while(i<len_a){
        scanf("%d", &e1);
        ListInsert(&La, ++i, e1);
    }
    
    int j = 0, e2 = 0;
    printf("请输入顺序表 Lb 的各元素(非递减顺序):\n");
    while(j<len_b){
        scanf("%d", &e2);
        ListInsert(&Lb, ++j, e2);
    }
    
    DataJudge(La); //判断输入数据是否非递减
    DataJudge(Lb);
    
    MergeList_Sq(La, Lb, &Lc); //合并
    PrintMergedList_Sq(&Lc); //输出
    return 0;
}

运行结果示例：



（输入格式正确的情况）



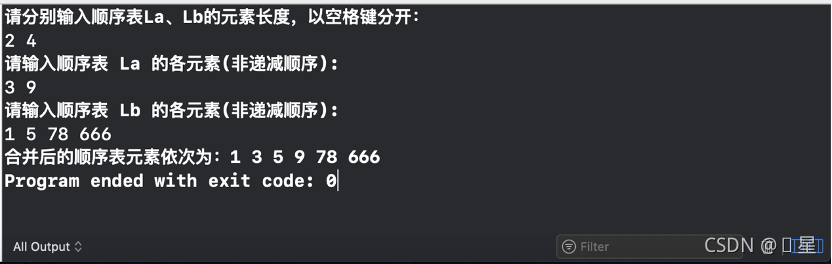
（输入格式错误的情况）




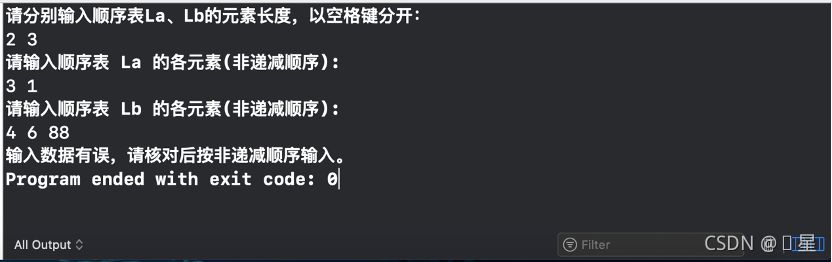
2、用 LinkList 类型自行建立两个有序的单链表，然后将其合并成一个新的有序单链表（即实现算法2.12）。

#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
//实现将两个单链表 La、Lb 的合并，储存于 La 中
typedef struct LNode{
    int data;
    struct LNode *next;
} LNode, *LinkList;

//初始化 L，分配内存
LinkList InitList_L(LinkList L){
    return (LinkList)malloc(sizeof(LNode));
}

//输入元素，创建链表
void CreatLink_L(LinkList L, int n){
    int temp = 0;
    LinkList p = L;
    while(n--){
        LinkList q = (LinkList)malloc(sizeof(LNode));
        q->next = NULL;
        scanf("%d", &temp);
        q->data = temp;
        p->next = q;
        p = p->next;
    }
}

//输出单链表
void PrintList(LinkList L){
    L = L->next;
    while(L){
        printf("%d ", L->data);
        L = L->next;
    }
    printf("\n");
}

//有序单链表合并
LinkList MergeList_L(LinkList La, LinkList Lb){
    LinkList pa, pb, pc;
    pa = La->next;
    pb = Lb->next;
    pc = La;
    LinkList Lc = pc;
    while(pa && pb){
        if(pa->data <= pb->data){
            pc->next = pa;
            pc = pa;
            pa = pa->next;
        }
        else{
            pc->next = pb;
            pc = pb;
            pb = pb->next;
        }
    }
    pc->next = pa ? pa : pb;
    pc->next->next = NULL;
    return Lc;
}

int main() {
    int m = 0, n = 0;
    LinkList La, Lb, Lc;
    La = InitList_L(La);
    Lb = InitList_L(Lb);
    Lc = InitList_L(Lc);
    
    printf("请分别输入单链表La、Lb的元素个数：\n");
    scanf("%d %d", &m, &n);
    
    printf("请依次输入 La 的元素（非递减顺序）：\n");
    CreatLink_L(La, m);
    printf("请依次输入 Lb 的元素（非递减顺序）：\n");
    CreatLink_L(Lb, n);
    
    Lc = MergeList_L(La, Lb);
    
    printf("合并后的链表元素依次为：\n");
    PrintList(Lc);
    return 0;
}

运行结果示例：






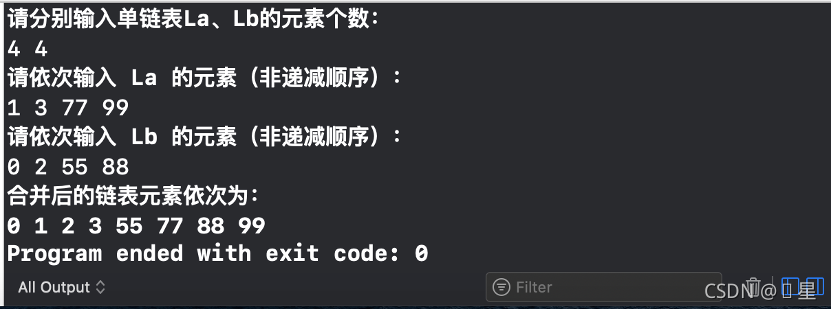
3、分别分析有序的顺序表合并，和有序的单链表合并的算法时间复杂度。


答：

• 假设顺序表La、Lb的元素数量分别为：m、n，单链表La、Lb的元素数量分别为：x、y。
• 由于算法中，对两个顺序表（单链表）中的元素，在进行相互比较这一操作时，每个元素是否立即插入合并后的新表这个判断语句只被遍历了一遍，故时间复杂度为两个表的元素数量之和。
• 则：
  
  顺序表合并的时间复杂度 O(n) = m + n .
  
  单链表合并的时间复杂度 O(n) = x + y .