1.自己实现迪杰斯特拉算法
function[P,d] = Dijkstra(G,start,End)
% 建立权重矩阵
% 判断是否存在权重矩阵,如果不存在,那么默认权重为1
[n,m] = size(G.Edges);x = length(unique(G.Edges.EndNodes));
W(1:x,1:x) = inf;W(logical(eye(size(W)))) = 0; % 初始化权重矩阵W,对角线赋值为0
if m ==1
for i = 1:n
W(G.Edges.EndNodes(i,1),G.Edges.EndNodes(i,2)) = 1;
try
if class(G) == 'graph' % 如果为有向图,那么该权重矩阵为对称
W(G.Edges.EndNodes(i,2),G.Edges.EndNodes(i,1)) = W(G.Edges.EndNodes(i,1),G.Edges.EndNodes(i,2));
end
end
end
elseif m == 2
for i = 1:n
W(G.Edges.EndNodes(i,1),G.Edges.EndNodes(i,2)) = G.Edges.Weight(i);
try
if class(G) == 'graph' % 如果为有向图,那么该权重矩阵为对称
W(G.Edges.EndNodes(i,2),G.Edges.EndNodes(i,1)) = W(G.Edges.EndNodes(i,1),G.Edges.EndNodes(i,2));
end
end
end
end
% 建立距离矩阵Distend 父节点矩阵Parent 是否已访问矩阵Visit
% 初始化距离矩阵,默认初始距离为无穷,起始点距离为0
D(1,1:x) = inf;D(1,start) = 0;D_ = D; % D_为D的傀儡
% 初始化父节点矩阵为0
Parent = zeros(1,x);
% 初始化访问矩阵 为访问完成为0,访问完成为1
Visit = zeros(1,x);
% 计算起始点到每个点的最短距离
for i = 1:x
[~,index] = min(D_);
for j = 1:x
if W(index,j) ~= inf && W(index,j) ~= 0 && Visit(j) == 0
distent = W(index,j) + D(index);
if distent < D(j)
D(j) = distent;D_(j) = distent;
Parent(j) = index; % 更新父节点
end
end
end
Visit(index) = 1;D_(index) =inf; %这里把已访问过的节点距离设为inf方便之后查询D的最短路径时排除已访问过的节点
end
% 得到最短路径
d = D(End);
% 得到父节点们
% 初始化路径
P = [];
p = Parent(End);
for i = 1:x
if any(P==start) == 0
P(1,i) = p;
p = Parent(p);
end
end
P = fliplr(P);P(1,end+1) =End;
end
实现效果
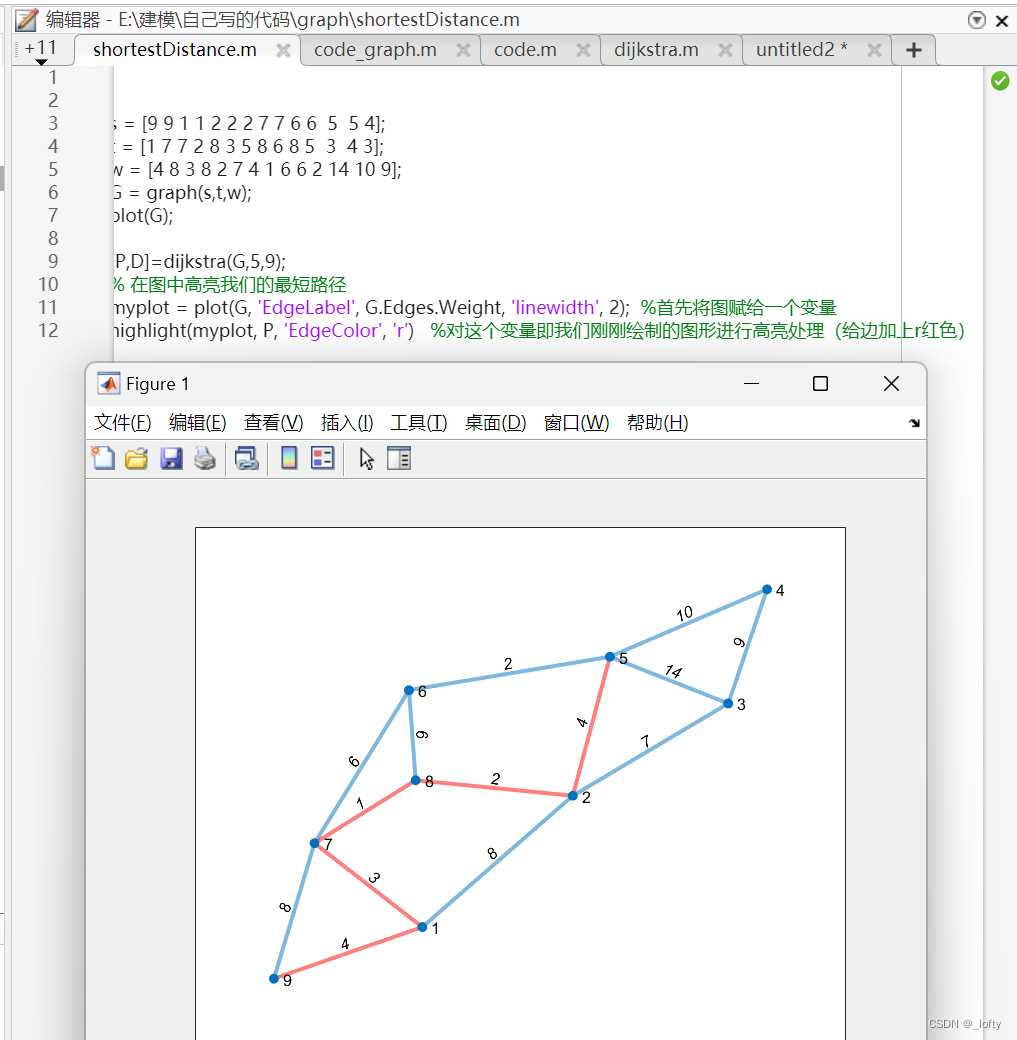
2.作业
% 构造带权有向图
s=[1 1 1 2 3 3 4 5 5 5 5 6 6 7 9 9];
t=[2 3 4 5 2 4 6 4 6 7 8 5 7 8 5 8];
w=[6 3 1 1 2 2 10 6 4 3 6 10 2 4 2 3];
G=digraph(s,t,w);
% 绘制图
plot(G,'EdgeLabel',G.Edges.Variables);
set(gca,'XTick',[],'YTick',[]);
% 找出最短路径
[P,D]=shortestpath(G,1,8,'Method','positive');
% 高亮显示最短的那条路
shortest = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2);
highlight(shortest, P, 'EdgeColor', 'r');
实现效果
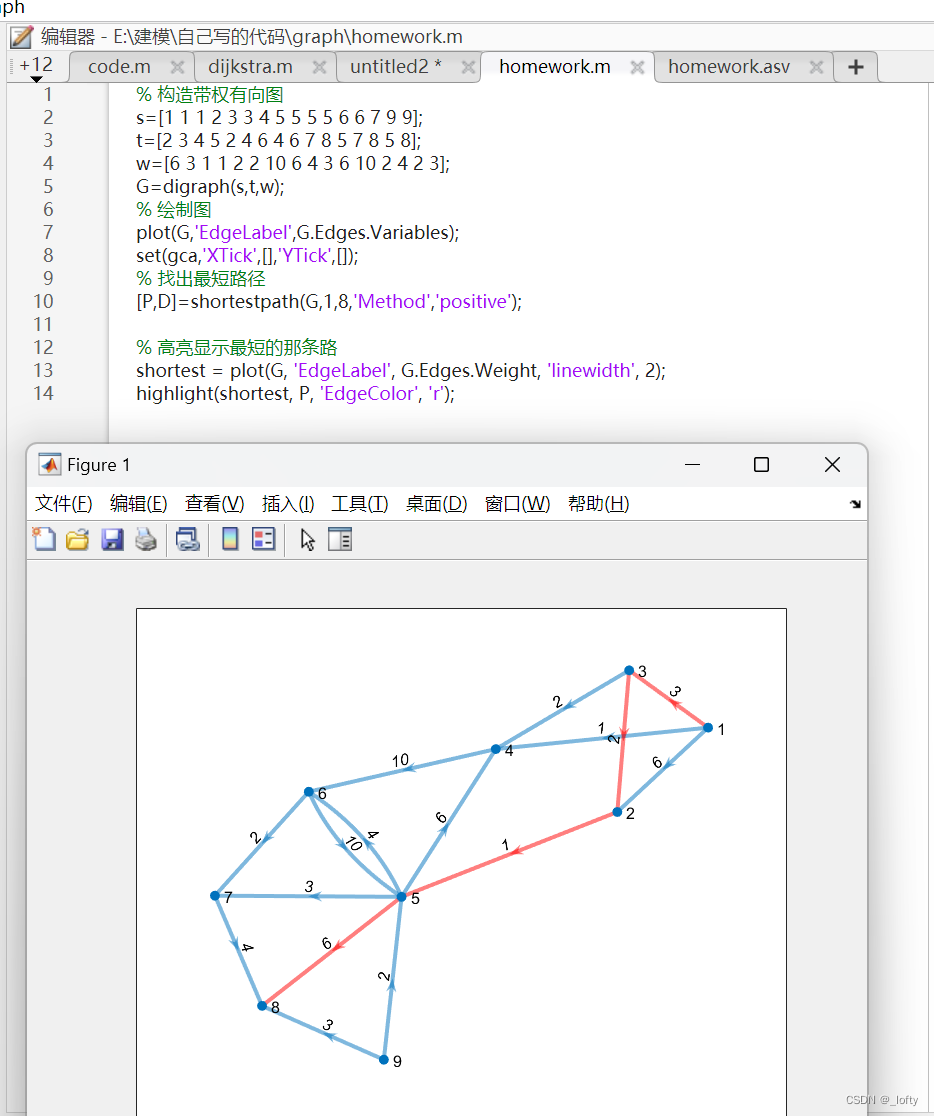
版权声明:本文为qq_52641289原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。