1、计算机为什么使用二进制:
1.计算机的元器件晶体管只有 2 种状态,
通电(1)&断电(0)
,用二进制可直接根据元器件的状态来设计计算机。
2.而且,数学中的“布尔代数”分支,可以用 True 和 False(可用 1 代表 True,0 代表 False)进行逻辑运算,代替实数进行计算。
3.计算的状态越多,信号越容易混淆,影响计算。对于当时每秒运算百万次以上的晶体管,信号混淆是特别让人头疼的的。
2、布尔代数&布尔代数在计算机中的实现
-
变量:没有常数,仅
True 和 False
这两个变量。 -
三个基本操作:
NOT/AND/OR
。 - 为什么称之为“门”:控制电流流过的路径
实现方式
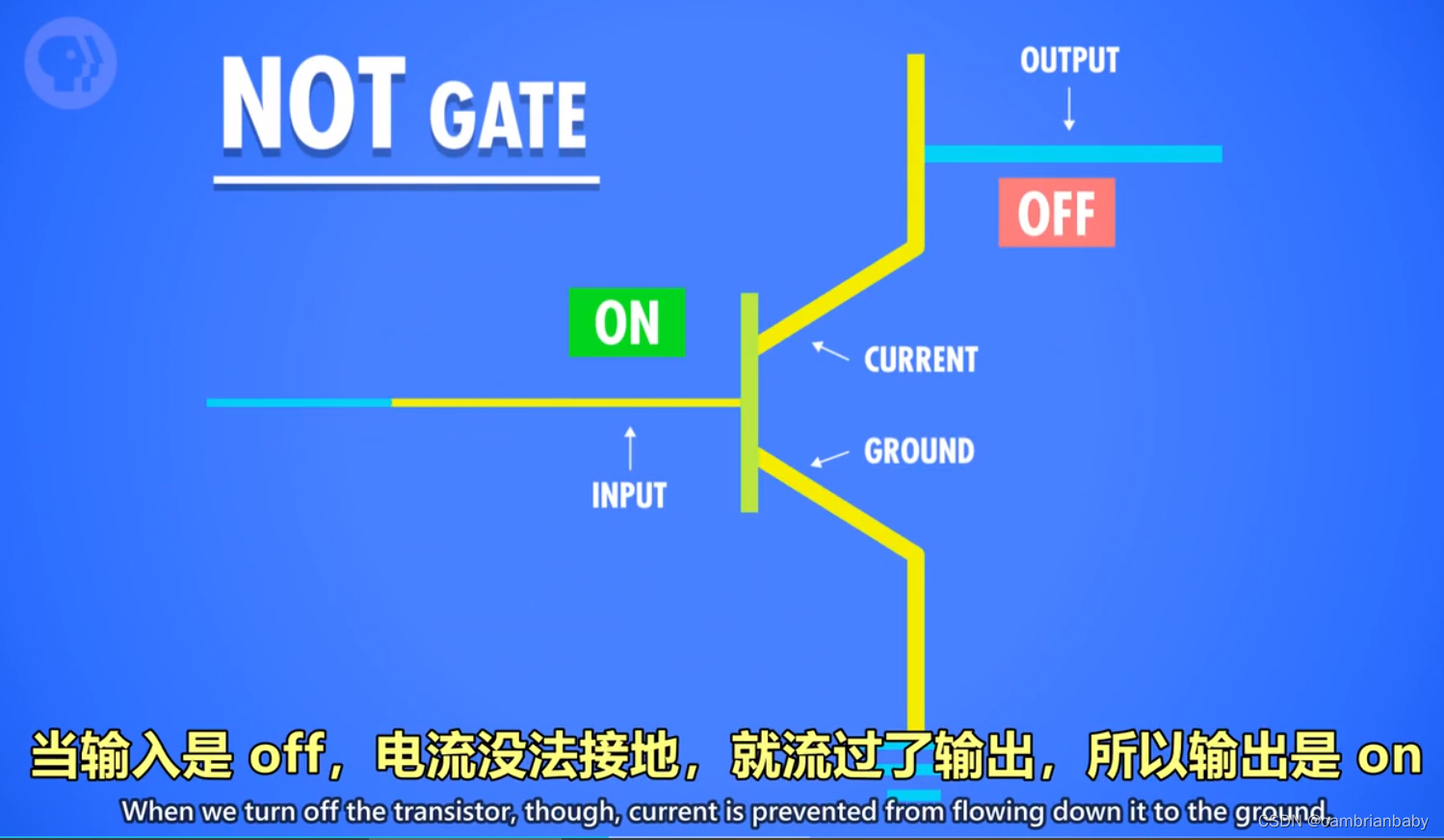
1)NOT 操作:
1 命名:称为 NOT 门/非门。
2 作用:
将输入布尔值反转。输入的 True 或 False
,输出为 False 或 True。
3 晶体管的实现方式:
- 半导体通电 True,则线路接地,无输出电流,为 False。
- 半导体不通电 False,则输出电流从右边输出,为 True
-
2)AND 操作
1 命名:AND 门/与门
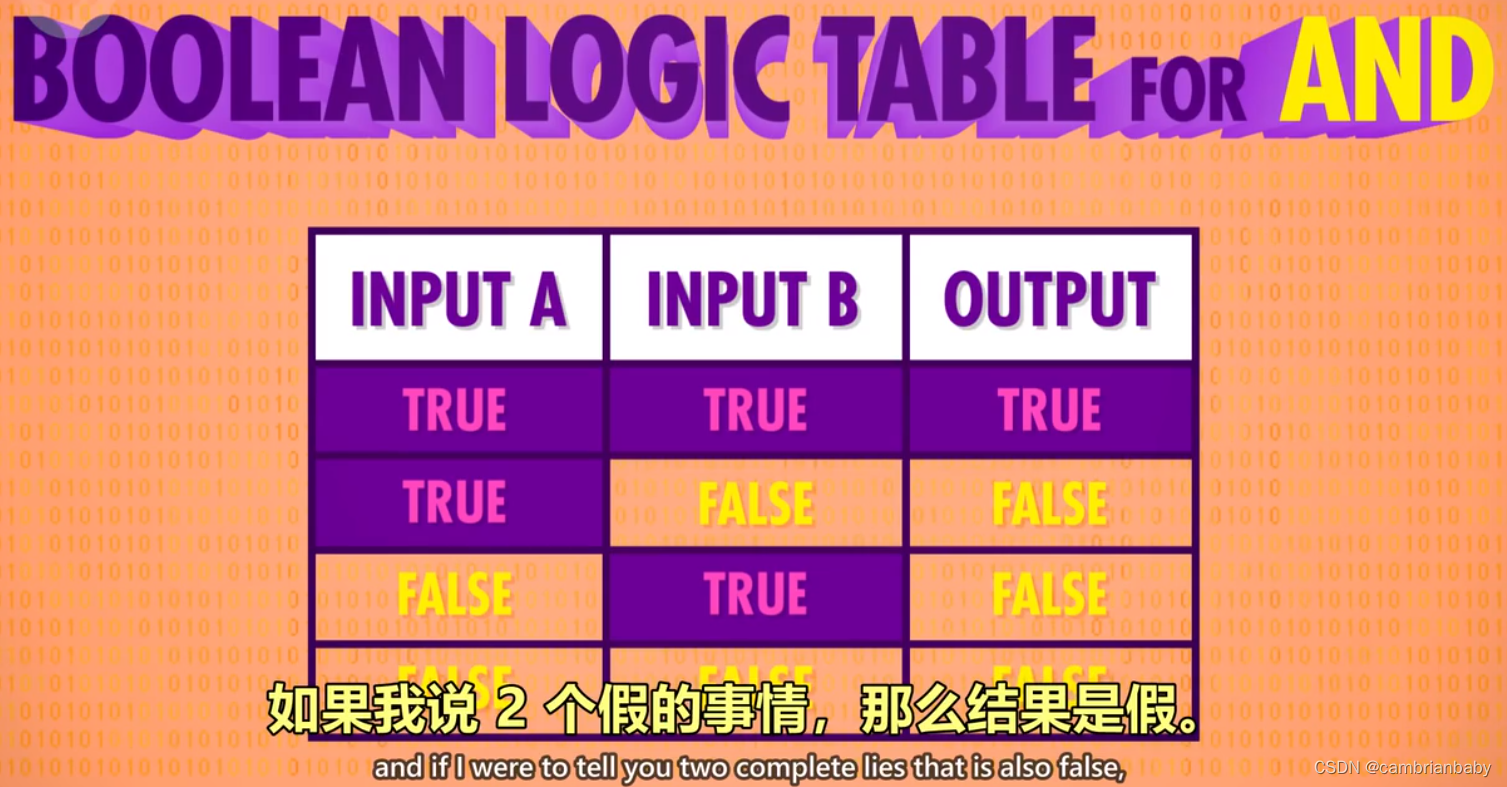
2 作用:
由 2 个输入控制输出,仅当 2 个输入 input1 和 input2 都为 True 时,输出才为 True,2 个输入的其余情况,输出均为 False。
*可以理解为,2 句话(输入)完全没有假的,整件事(输出)才是真的。
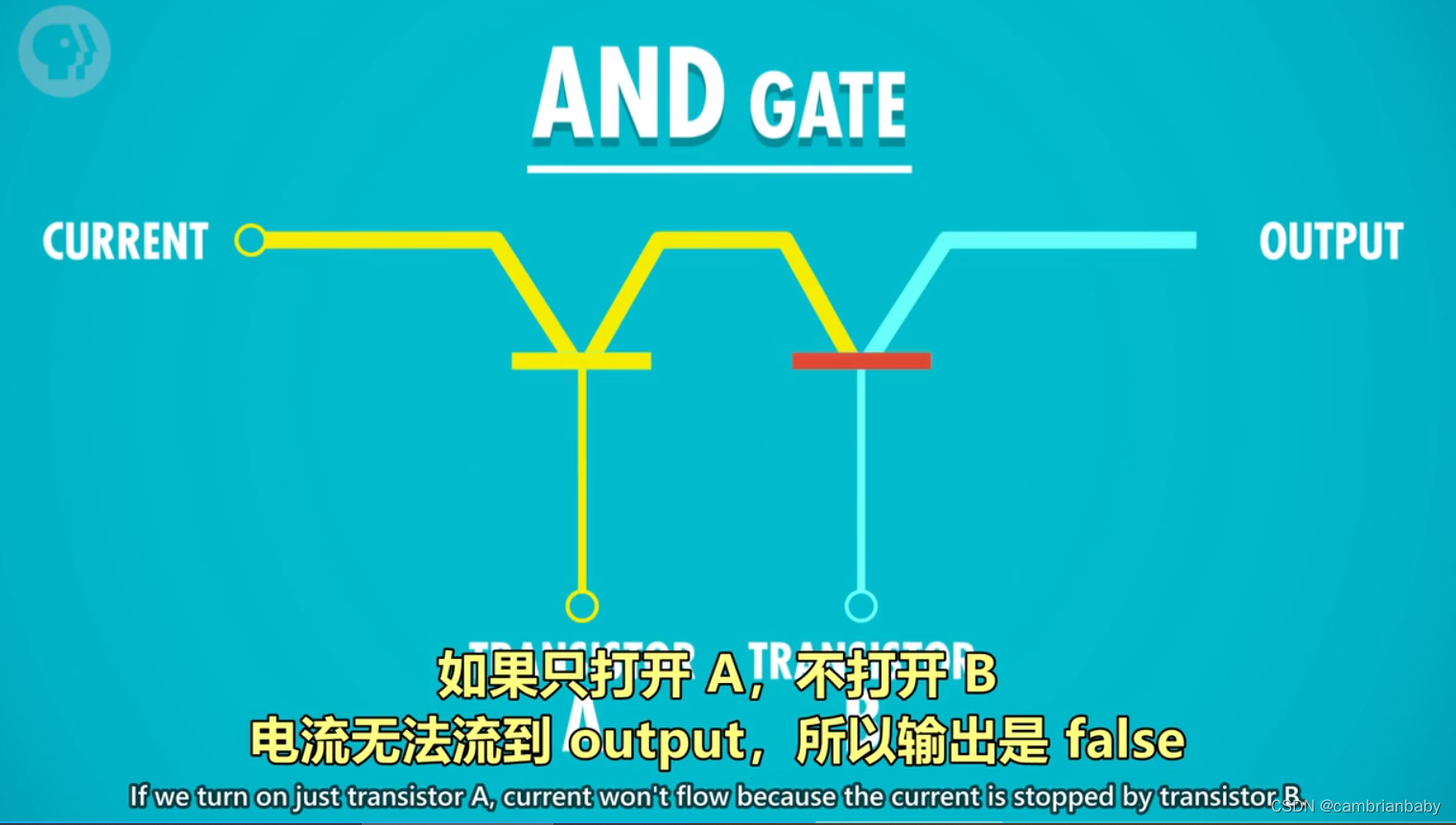
3 用晶体管实现的方式:
串联两个晶体管,仅当 2 个晶体管都通电,输出才有电流(True)
3)OR 操作
1 命名:OR 门/或门
2 作用:由 2 个输入控制输出,只要其中一个输入为 True,则输出 True。

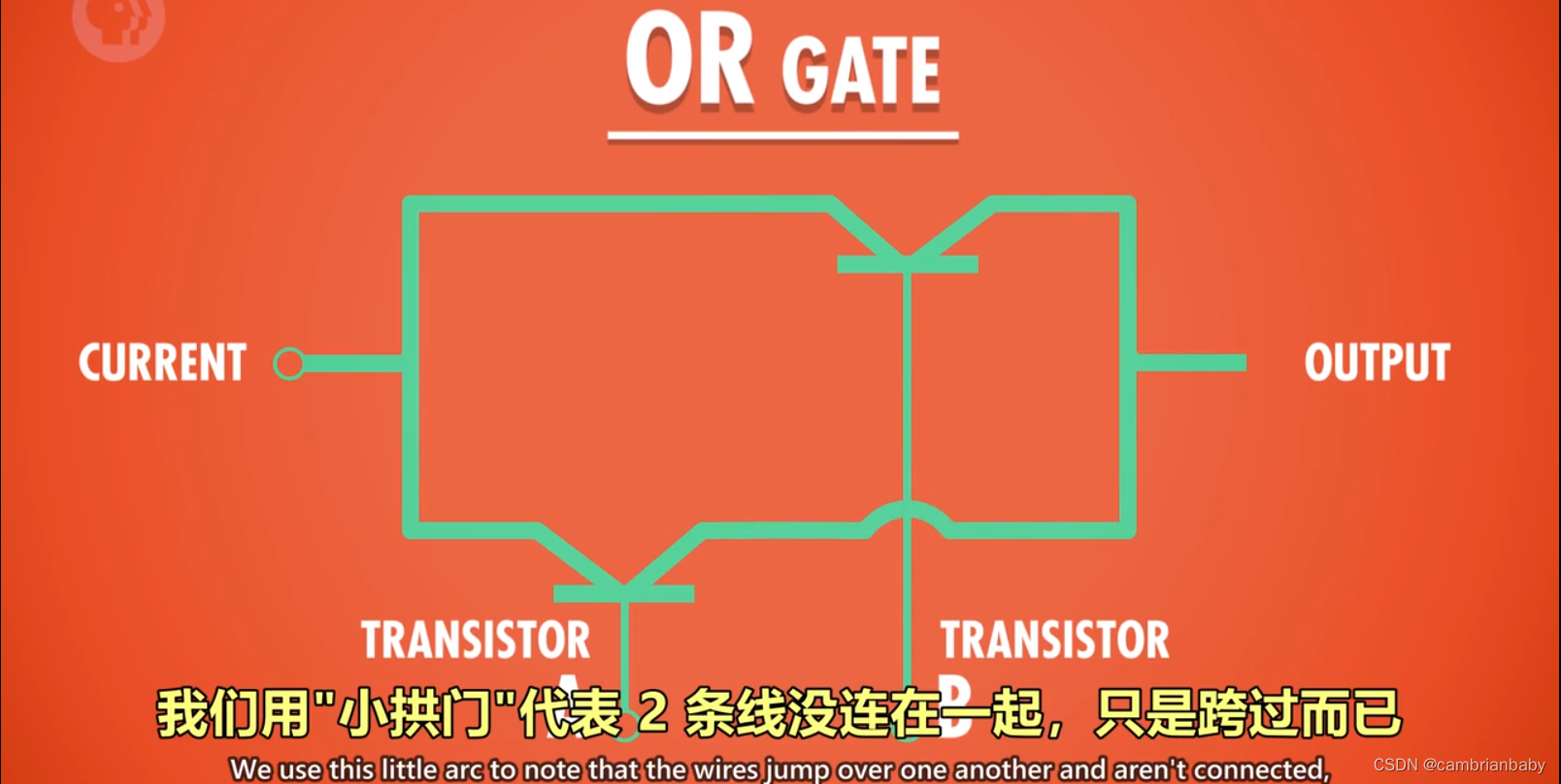
3 用晶体管实现的方式:
使用 2 个晶体管,将它们并联到电路中,只要有一个晶体管通电,则输出有电流(True)
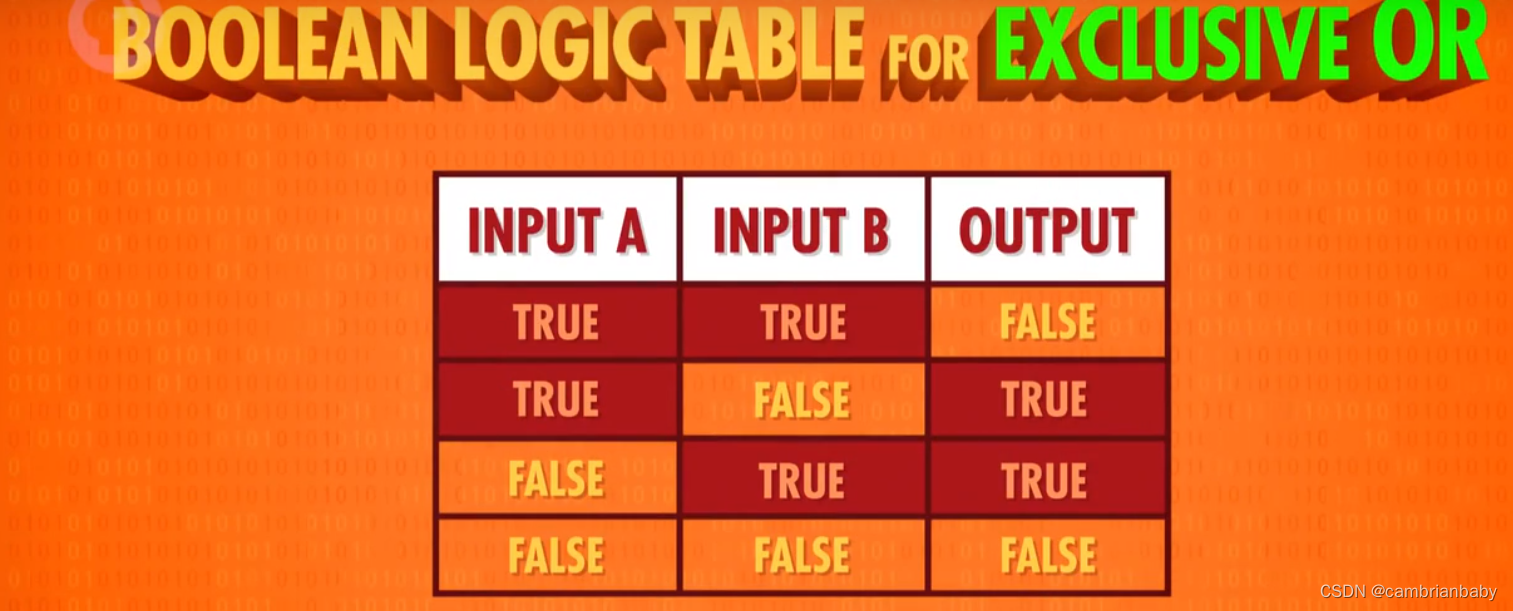
3、特殊的逻辑运算——异或
1 命名:XOR 门/异或门
2 作用:
2 个输入控制一个输出。当 2 个输入均为 True 时,输出 False,其余情况与 OR 门相同。
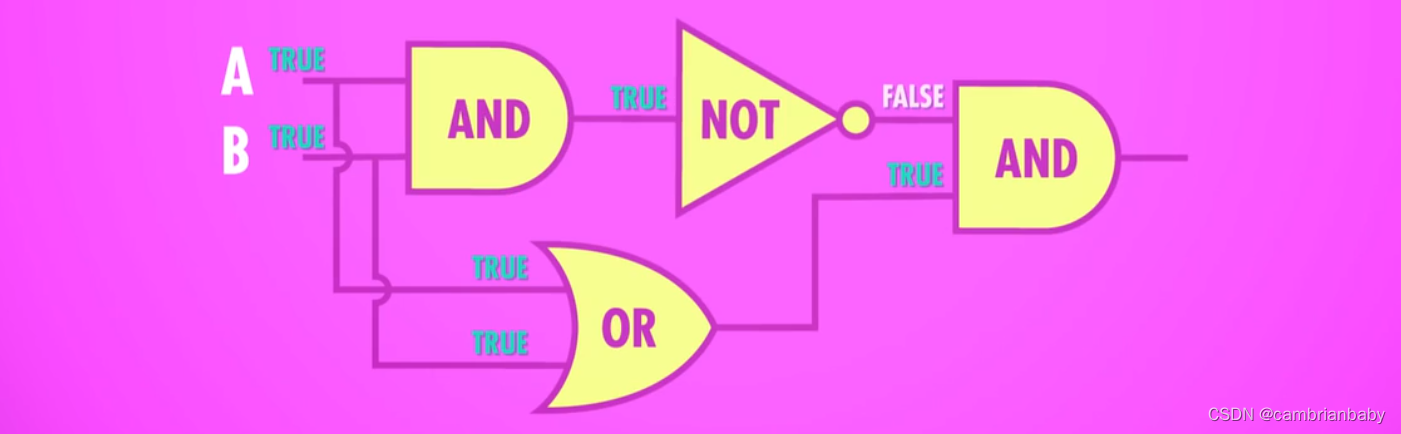
3 图示:
先用一个 OR 门,将其与 AND 门并联,AND 门与 NOT 门串联,最后让 NOT 与 AND 门并联,获得输出。
4、逻辑门的符号表示
1 作用:将逻辑门简化,将逻辑门用于构建更大的组件,而不至于太复杂。
2 图示:
- 非门:用三角形+圆圈表示
- 与门:用 D 型图案表示
- 或门:用类似 D 向右弯曲的图案表示
- 异或门:用或门+一个圆弧表示
5、抽象的好处
使得分工明确,不同职业的工程师各司其职,而不用担心其他细节。