矩阵的QR分解和LU分解的目的都是为了便于矩阵计算。
矩阵的QR分解
概述
A
=
Q
R
A=QR
A=QR这一过程将矩阵分解为
Q
Q
Q和
R
R
R两部分,其中
Q
Q
Q是标准正交矩阵,
R
R
R是一个上三角矩阵。
矩阵的
Q
R
QR
QR分解能够简化计算可以以线性系统的计算为例,
A
x
=
b
⟹
(
Q
R
)
x
=
b
Ax=b\Longrightarrow (QR)x=b
Ax=b⟹(QR)x=b
Q
−
1
Q
R
x
=
Q
−
1
b
⟹
R
x
=
Q
T
b
Q^{-1}QRx=Q^{-1}b\Longrightarrow Rx=Q^Tb
Q−1QRx=Q−1b⟹Rx=QTb
Q
T
Q^T
QT是非常好计算的,
R
R
R是一个上三角矩阵(相当于Gauss-Jordan消元法的前向过程结束),从下往上推就可以很快计算出线性系统的结果。
因为涉及到求取标准正交矩阵
Q
Q
Q的过程,所以矩阵
A
A
A可以进行
Q
R
QR
QR分解的条件是
A
A
A的各个列向量是线性无关的。因为只有满足这一点才能进行Gram-Schmidt过程。
演示分析
A
=
Q
R
,
其
中
A
=
(
a
1
⃗
,
a
2
⃗
,
.
.
.
,
a
n
⃗
)
A=QR,其中A=(\vec{a_1},\vec{a_2},…,\vec{a_n})
A=QR,其中A=(a1,a2,...,an)
对矩阵
A
A
A的各列执行Gram-Schmidt过程,得到正交向量
p
1
⃗
,
p
2
⃗
,
.
.
.
,
p
n
⃗
\vec{p_1},\vec{p_2},…,\vec{p_n}
p1,p2,...,pn,归一化后得到标准正交向量
q
1
⃗
,
q
2
⃗
,
.
.
.
,
q
n
⃗
\vec{q_1},\vec{q_2},…,\vec{q_n}
q1,q2,...,qn。
p
1
⃗
=
a
1
⃗
\vec{p_1}=\vec{a_1}
p1=a1
p
2
⃗
=
a
2
⃗
−
a
2
⃗
⋅
p
1
⃗
∣
∣
p
1
⃗
∣
∣
2
⋅
p
1
⃗
\vec{p_2}=\vec{a_2}-\frac{\vec{a_2}\cdot \vec{p_1}}{||\vec{p_1}||^2}\cdot\vec{p_1}
p2=a2−∣∣p1∣∣2a2⋅p1⋅p1
得到上三角矩阵
R
R
R的过程如下,以
A
A
A矩阵前3个列向量为例,
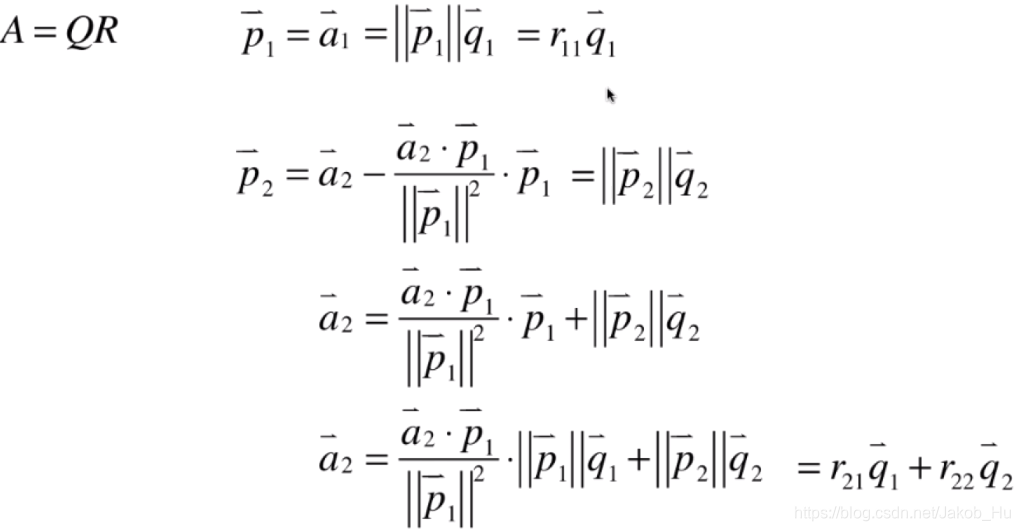
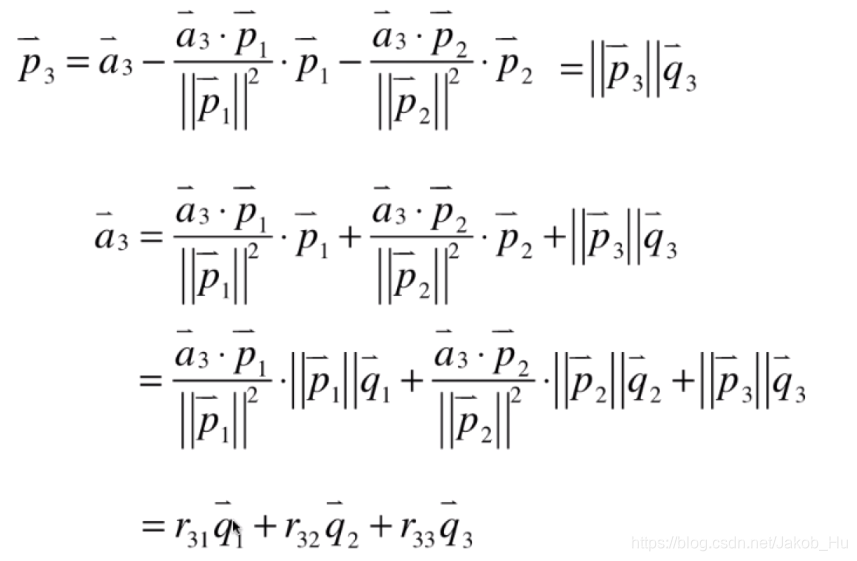
求取
R
R
R的过程是使用已经求取的标准正交基反推原来的列向量。每一个系数都是可以找到规律的。故矩阵的
Q
R
QR
QR分解实际上将矩阵A分解为如下形式,
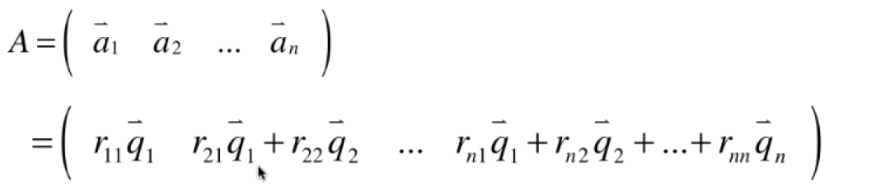
可以对该矩阵再进行推导,
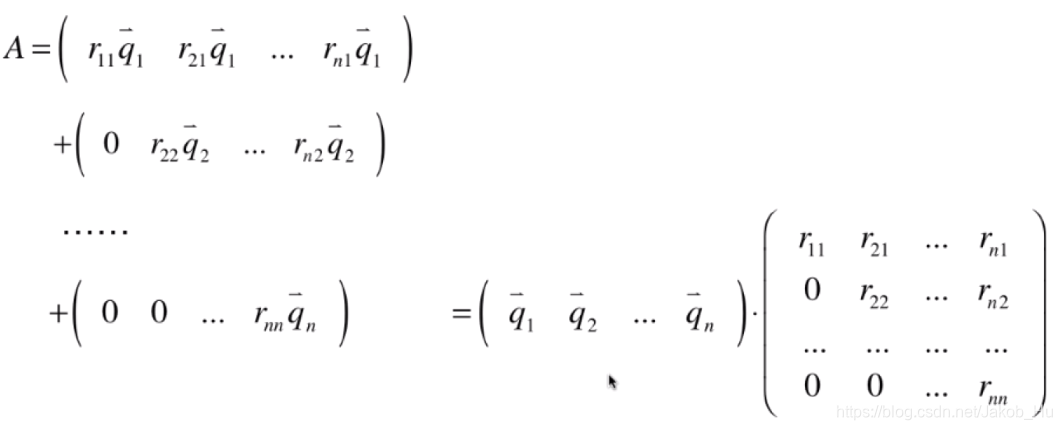
实现QR分解
上面的推导过程很复杂,但是在实际的计算过程中根本不需要求取
R
R
R中的每个值,而是只需通过Gram-Schmidt过程得到
A
A
A的标准正交矩阵
Q
Q
Q,很快速的求取出
R
R
R,通过如下形式,
A
=
Q
R
⟹
Q
−
1
A
=
R
A=QR\Longrightarrow Q^{-1}A=R
A=QR⟹Q−1A=R
由正交矩阵性质可得,
R
=
Q
−
1
A
⟹
R
=
Q
T
A
R=Q^{-1}A\Longrightarrow R=Q^TA
R=Q−1A⟹R=QTA
def qr(A):
"""
:param A: 一个矩阵对象,本节A是方阵,实际上一般矩阵也可以QR分解,只是本次不涉及
"""
assert A.row_num() == A.col_num(), "A must be square"
basis = [A.col_vector(i) for i in range(A.col_num())]
P = gram_schmidt_process(basis)
# 这里转置是因为在自定义的Matrix类中,是通过行向量创建矩阵的
Q = Matrix([v/v.norm() for v in P]).T()
R = Q.T.dot(A)
return Q, R
if __name__ == "__main__":
A = Matrix([[1, 1, 2], [1, 1, 0], [1, 0, 0]])
Q, R = qr(A)
print(Q.dot(R))