网络属性:如何衡量一个网络
关键网络属性:
- 度分布 P(k)
- 路径长度 h
- 聚类系数 C
- 连接单元 s
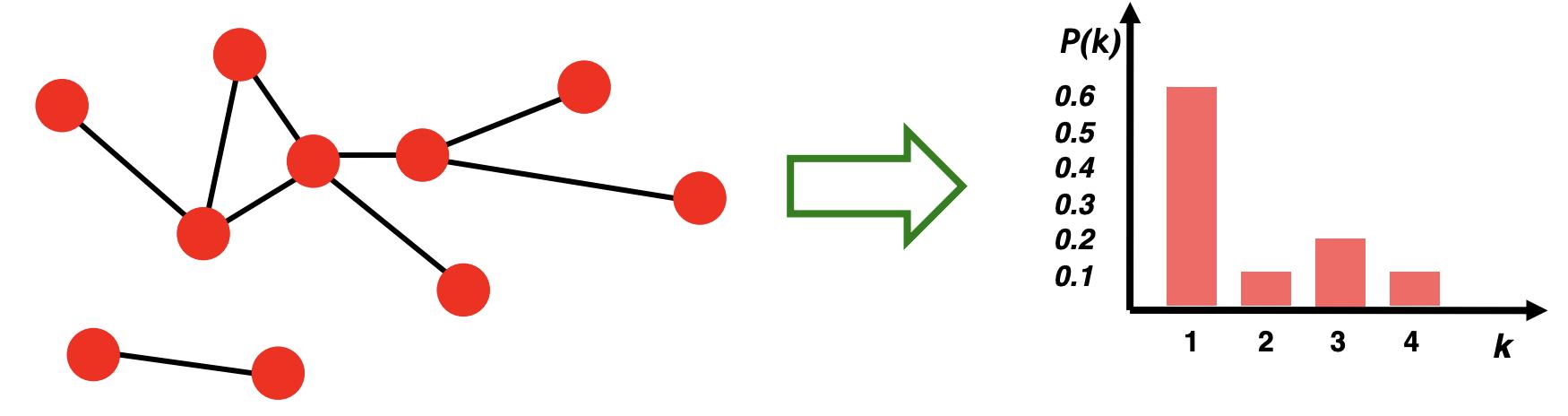
度分布 degree distribution
度分布 degree distribution
- 度分布P(k):
随机选择的节点的度数为k
Nk=#个度为k的节点 - 标准化直方图:
P(k)= Nk / N ➔ 图
图上的路径
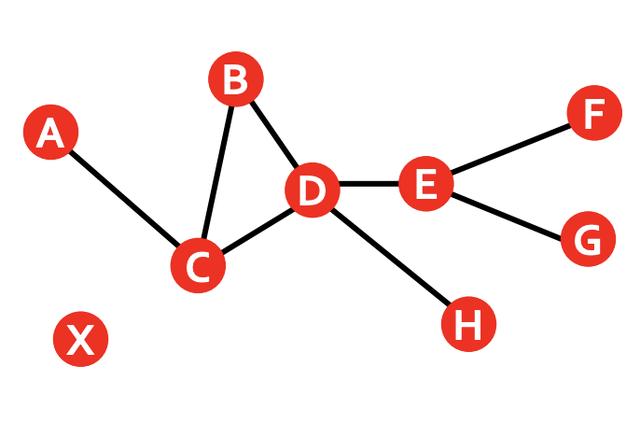
- 路径是一系列节点,其中每个节点链接到下一个节点
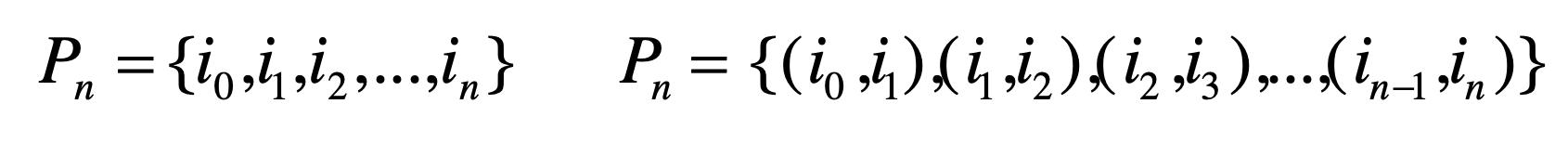
- 路径可以相交并多次通过相同边
- 例如:ACBDCDEG
距离
- 距离(最短路径,测地线)
一对节点之间的定义为沿边的数量连接节点的最短路径- 如果两个节点未连接,则距离通常定义为无限(或零)
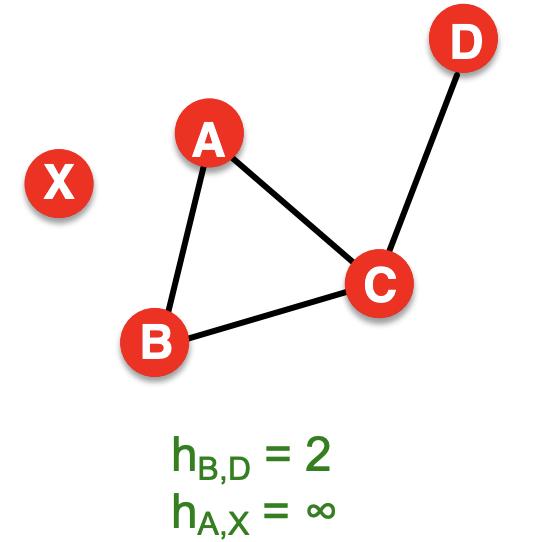
- 在有向图中,路径需要遵循箭头的方向
- 结果:距离为不对称:hB,C≠hC,B
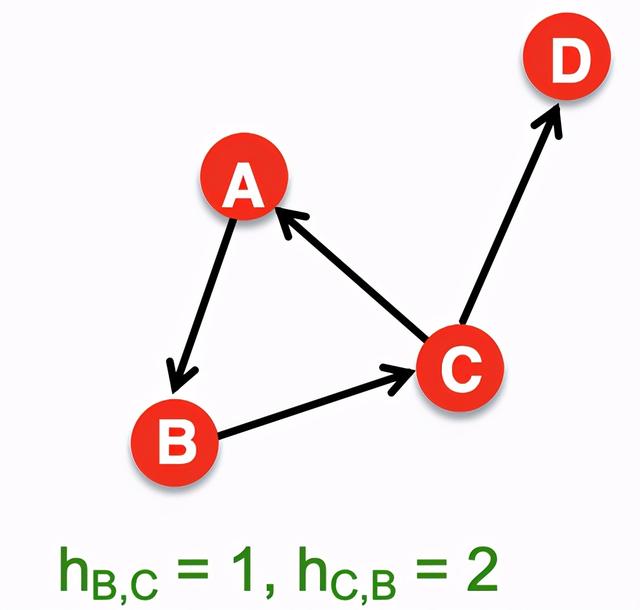
- 直径:最大(最短路径)图中任意一对节点之间的距离
- 平均路径长度:对于连接图形或者强连通有向图
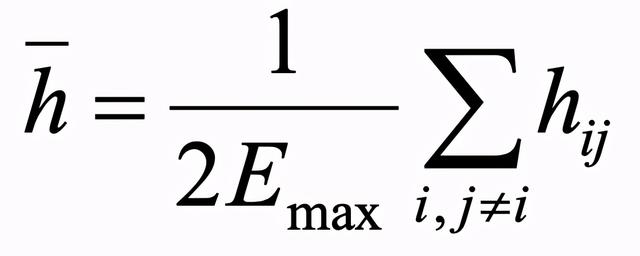
其中
- hij是从节点i到节点j的距离
- Emax是最大边数(总计节点对数)= n(n-1)/ 2
很多时候,我们仅计算连接的节点对(即,我们忽略“无限”长度路径)
请注意,此措施也适用于(强烈)连接图的组成部分
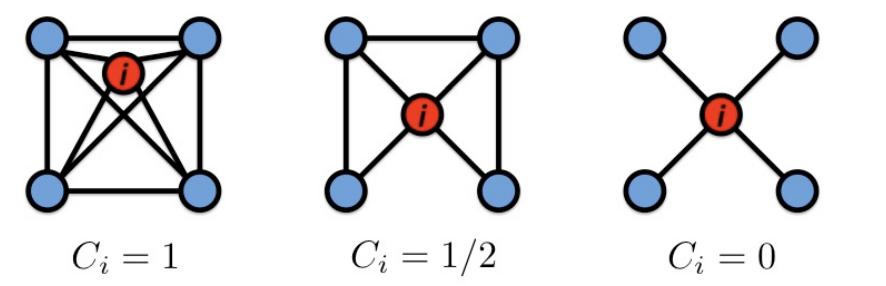
聚类系数
聚类系数(对于无向图):
- 节点i的邻居之间的联系如何?
- 节点i的度为ki
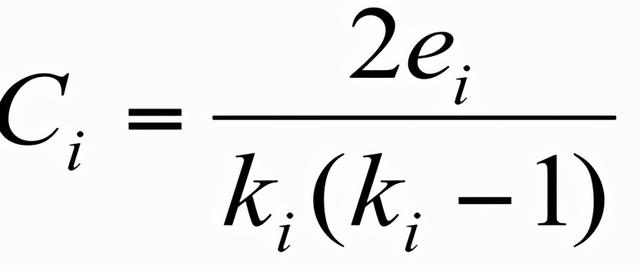
这里ei是节点i的邻接节点的边数。
平均聚类系数:
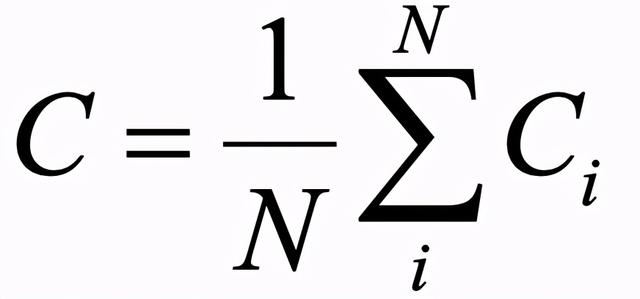
聚类系数(对于无向图):
- i的邻居之间的联系如何?
- 节点i的度为ki
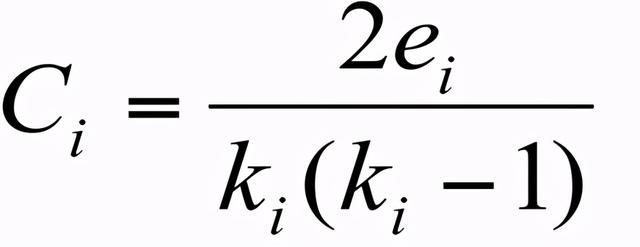
这里ei是节点i的邻接节点的边数。
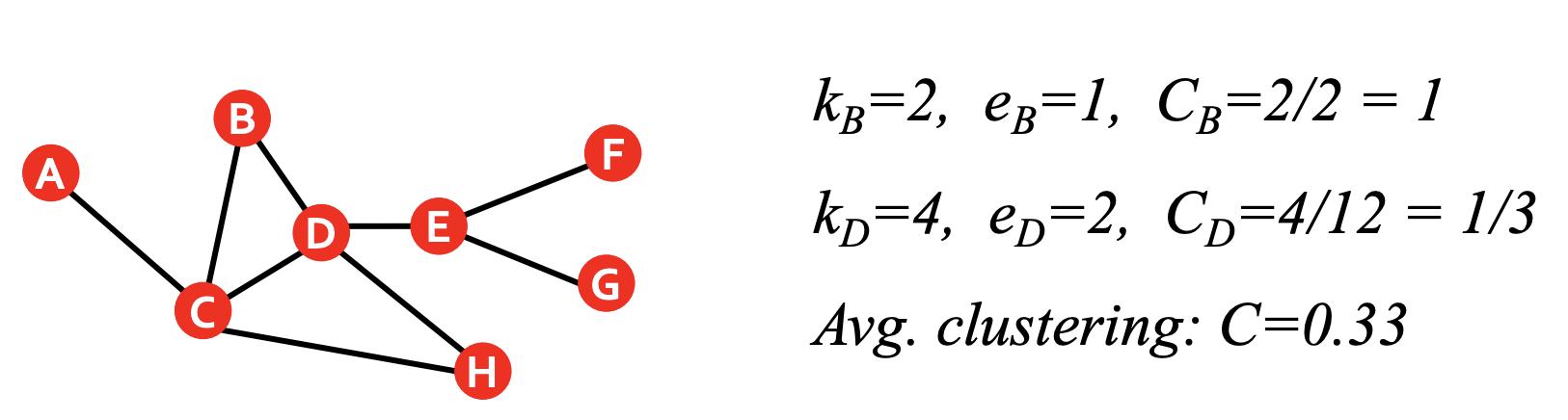
连接
- 最大连接组件的大小
- 通过一条路可以将任意两个顶点连接的最大的集合
- 最大组件=巨型组件
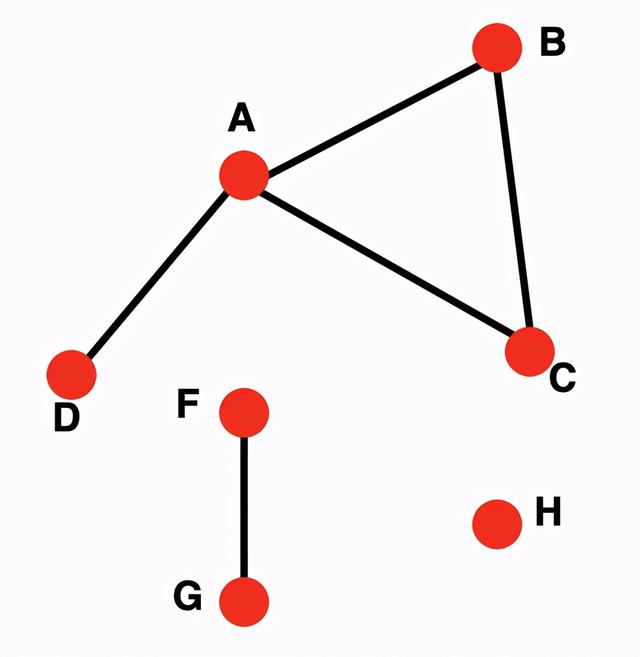
如何查找连接的组件:
•从随机节点开始执行,广度优先搜索(BFS)
•标记BFS访问的节点
•如果访问了所有节点,则说明网络已连接
•否则,找到一个未访问的节点并重复BFS
下面是一些现实世界的例子:
MSN的例子:
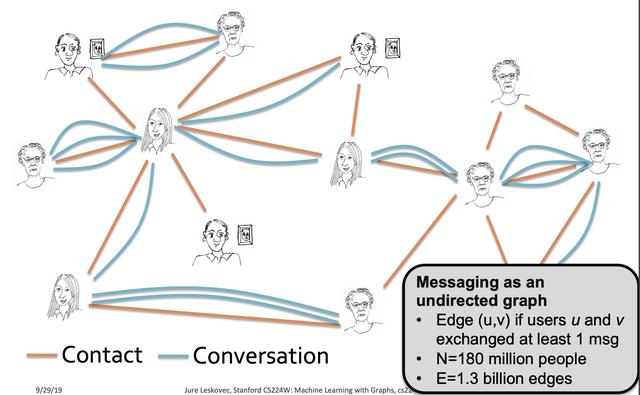
MSN网络的节点数是1.8亿
边数 13亿
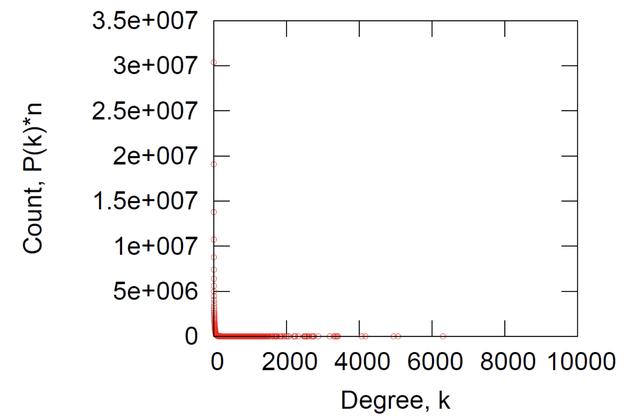
度分布
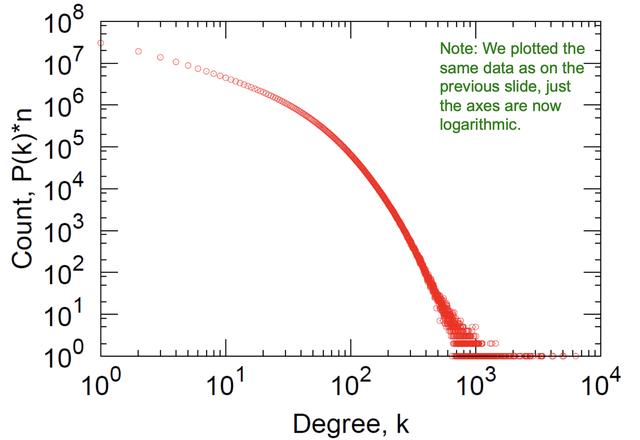
指数度分布
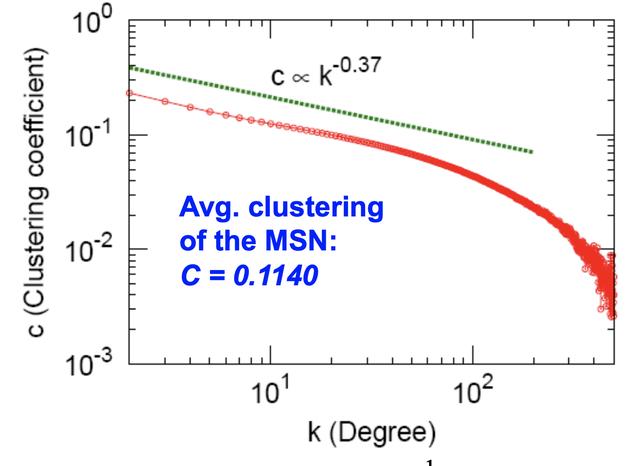
聚类系数
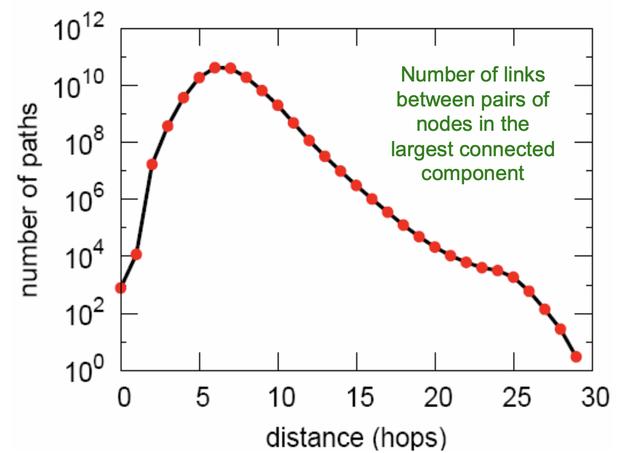
距离
随机图模型
图的简单模型
- Erdös-Renyi随机图[Erdös-Renyi,‘60]
- 两个变体:
- Gnp:n个节点上的无向图,其中每个节点边缘(u,v)出现概率为p
- Gnm:具有n个节点的无向图,并且m条随机均匀选择的边
随机图模型
- n和p不能唯一确定图!
- 该图是随机过程的结果
- 对于相同的n和p,我们可以给出许多不同的实现
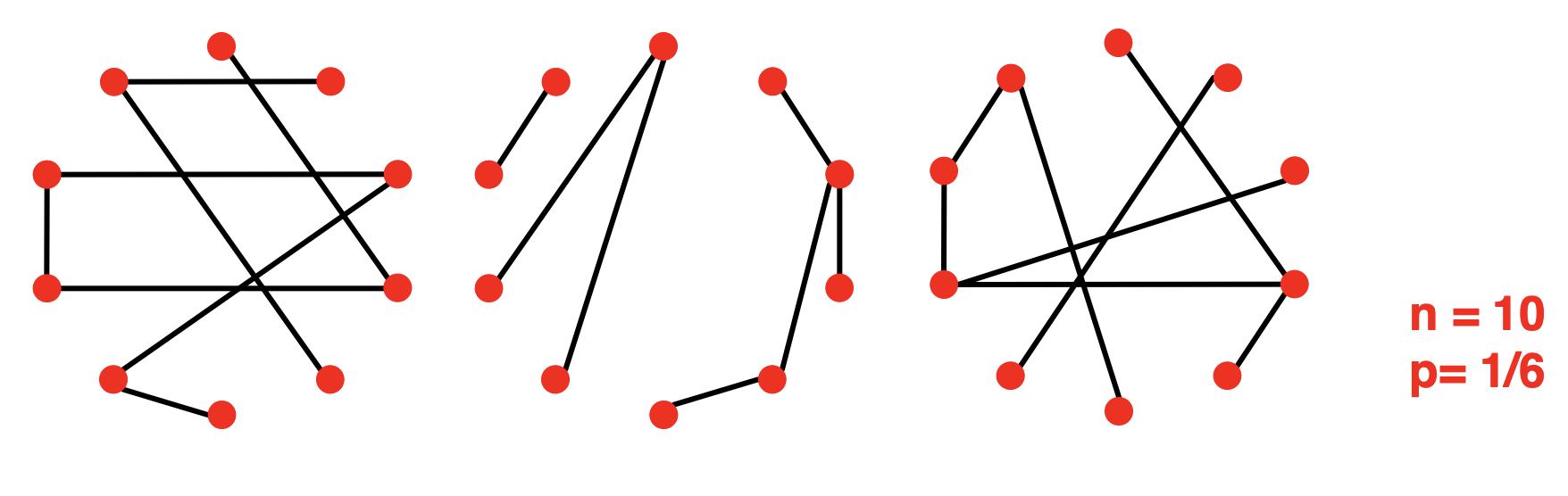
Gnp的度分布是二项式分布:
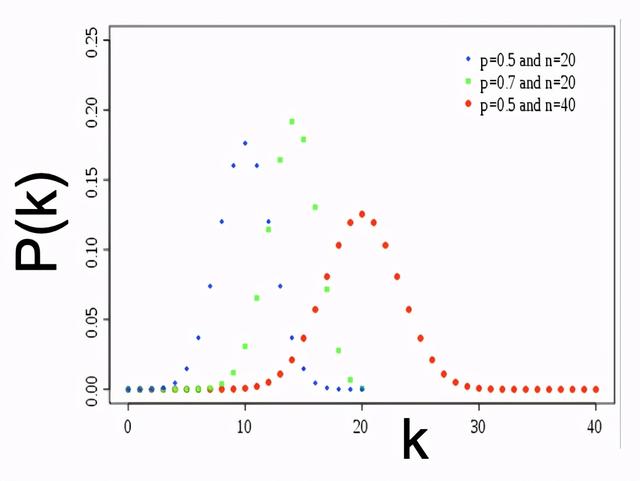
Gnp的聚类系数是:
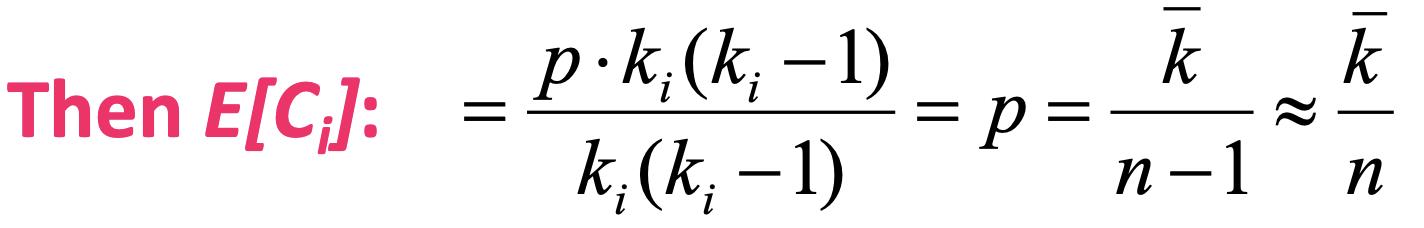
这个聚类系数是比较小的。
随着P的变化,Gnp的图结构的变化如下:

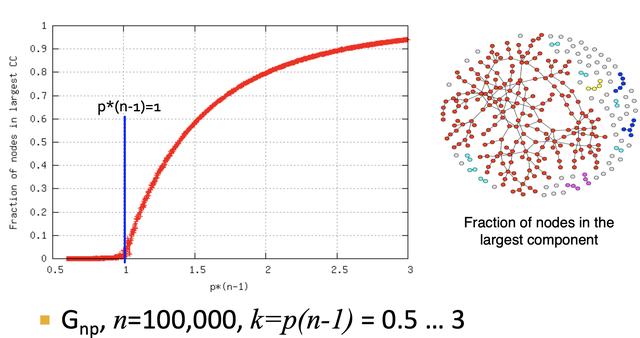
回到MSN的例子:

真实的网络像随机图吗?
- 巨型连接部件:[微笑]
- 平均路径长度:[微笑]
- 聚类系数:[发怒]
- 度分布:[发怒]
随机网络模型的问题:
- 度分布与实际网络不同
- 大多数实际网络中的巨型组件不会通过相变而出现
- 没有局部结构–聚类系数太低
最重要:真实网络是随机的吗?
答案很简单:不!
如果Gnp并不真实,为什么我们要花一些时间在它之上呢?
- 这是该课程其余部分的参考模型
- 这将帮助我们计算许多数量,然后与真实数据进行比较
- 这将有助于我们了解特定的属性是一些随机处理的结果
所以Gnp非常有用。
Small-World 问题
我们是否可以在拥有高聚集的同时拥有短的路径。
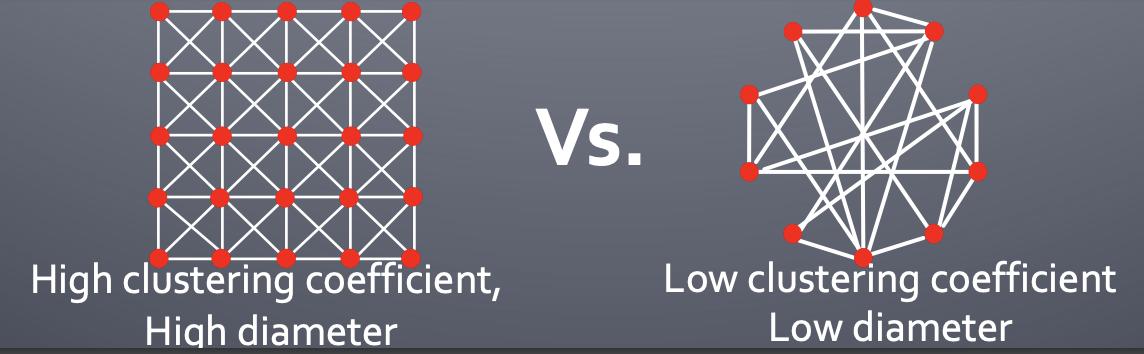
MSN网络聚类比相应的Gnp大7个数量级!
其它例子:
IMDB:N = 225,226个节点,平均度数 k = 61
电网:N = 4,941个节点,平均度数 k = 2.67
神经元网络:N = 282个节点,平均度数 k = 14
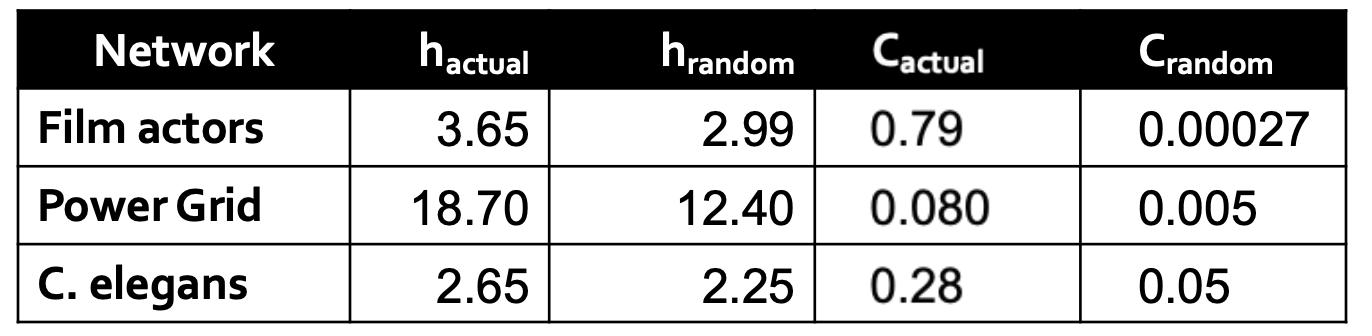
- h 是平均最短路径
- C 是聚类系数
- actual是实际网络
- random是随机图
扩张的后果:
- 短路径:O(log n)
- 如果我们保持度恒定,这是我们可以获得的最小直径
- 但是聚集系数很低
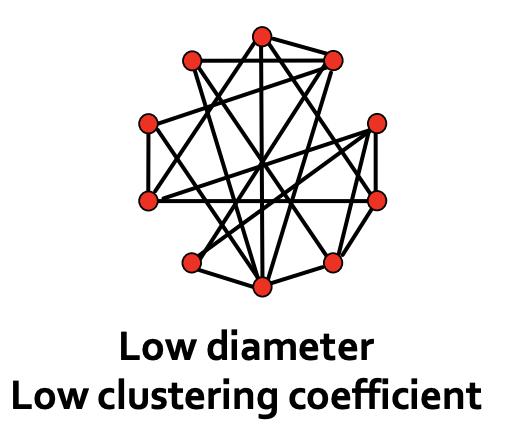
但是网络有“本地”结构:
- 三合会封闭:
- 朋友的朋友是我的朋友
- 高聚类但
- 直径也大
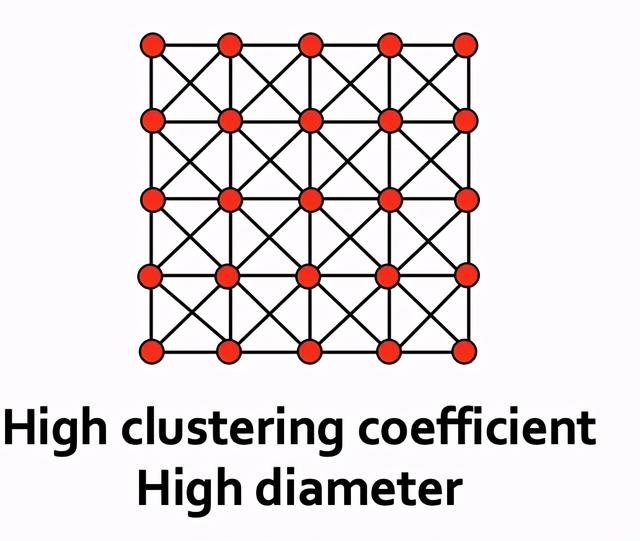
我们如何同时拥有高聚合但是短直径?
具有较高聚合的网络也可以是一个小世界(直径是对数logn)?
我们如何同时拥有高聚集和小直径?
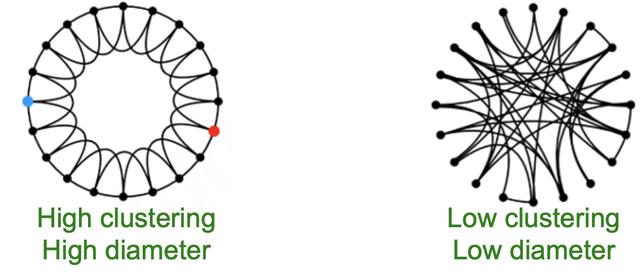
- 聚类意味着边缘的“局部性”
- 随机性实现“捷径”
解决方案:Small World 模型
小世界模型[Watts-Strogatz ‘98]
模型的两个组成部分:
- (1)从低维正则格子开始
- 在我们的例子中,我们使用环作为网络
- 聚类系数高
- (2)重新布线:引入随机性(“捷径”)
- 添加/删除边,以创建加入网络的远程部分
- 对于每个边,都有概率。 p,将另一个端点移至随机节点
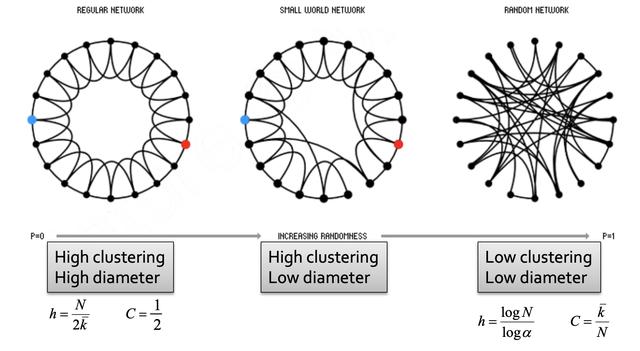
重新布线使我们能够在规则网络和随机图之间“过度”
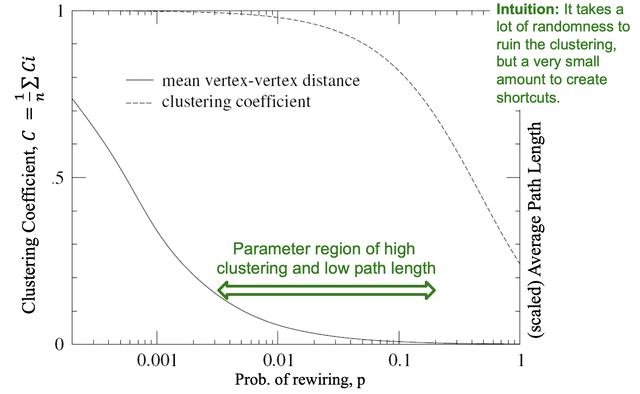
具有高群集的网络是否可以同时一个小世界?是的!您只需要几个随机链接
瓦特·斯特罗加兹(Watts Strogatz)模型:
- 提供有关聚类和小世界之间相互作用的见解
- 捕获许多现实网络的结构
- 真实网络的高度聚集
- 缺乏正确的度分配
Kronecker图模型:生成大型真实网络
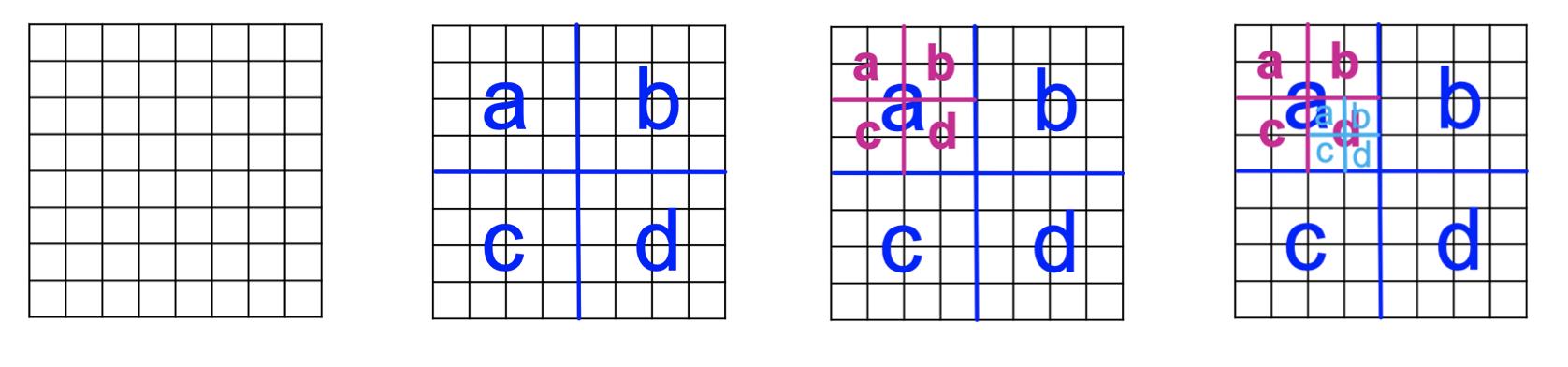
递归图生成:
我们如何递归地思考网络结构?直觉:自相似
- 对象类似于其自身的一部分:整体具有与一个或多个部分相同的形状
模仿递归图/社区增长:

Kronecker乘积是一种产生自相似矩阵的方法。
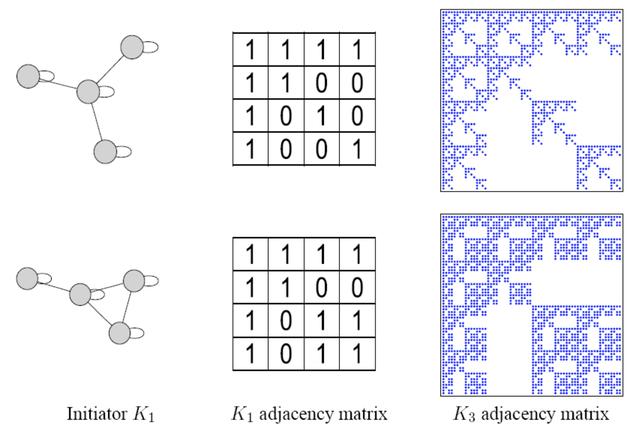
Kronecker图:网络结构的递归模型
矩阵A和B的Kronecker乘积为:
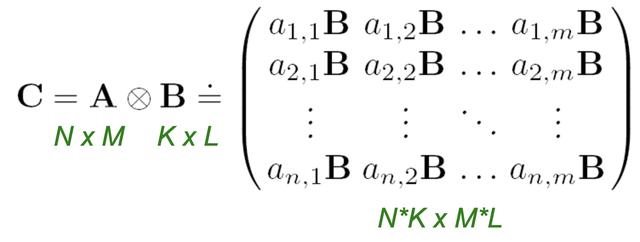
将两个图的Kronecker乘积定义为邻接矩阵的Kronecker乘积。
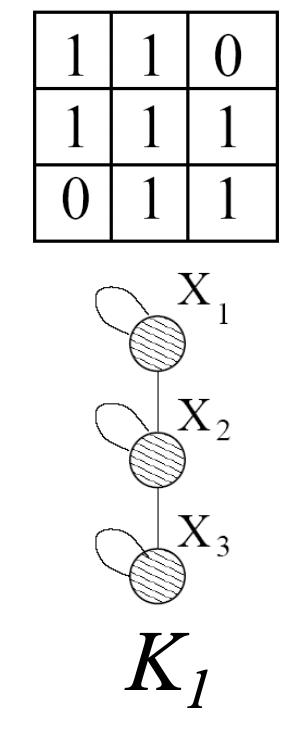
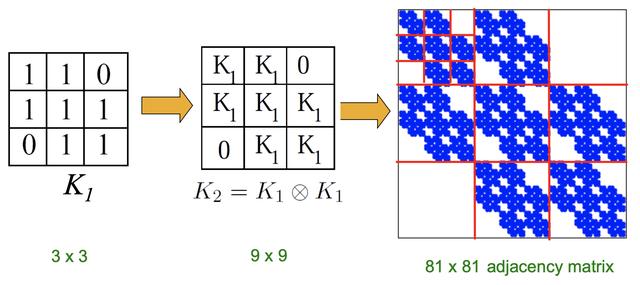
通过在初始矩阵Ki上迭代Kronecker乘积来增长图序列来获得Kronecker图:
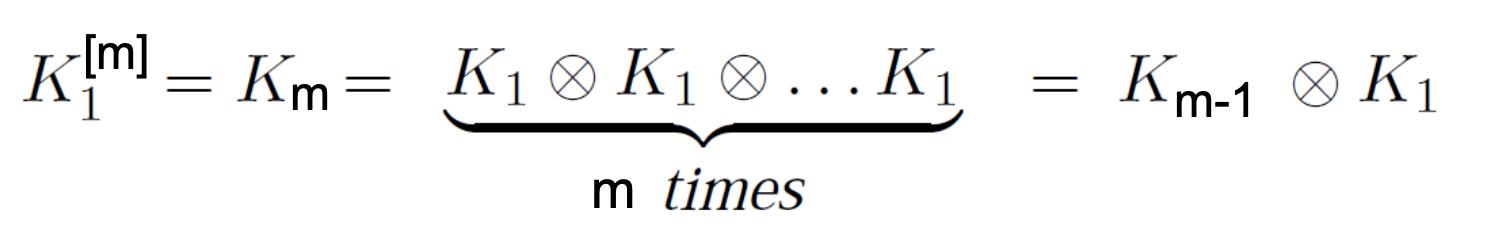
可以使用多个不同大小的初始矩阵。
随机Kronecker图
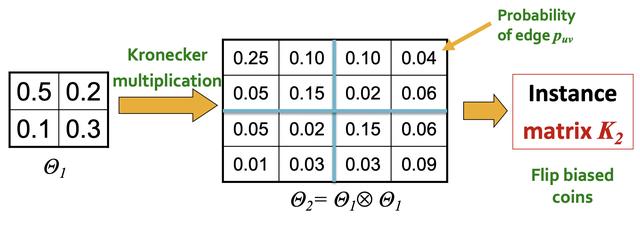
我们如何生成一个随机(定向)Kronecker图的实例?

想法:利用Kronecker图的递归结构,将边缘“拖放”到图形上
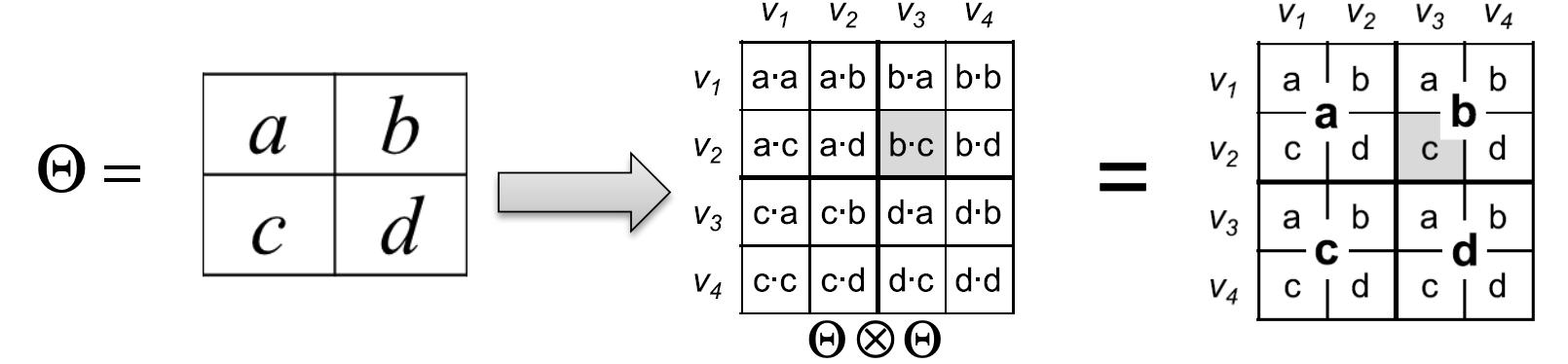
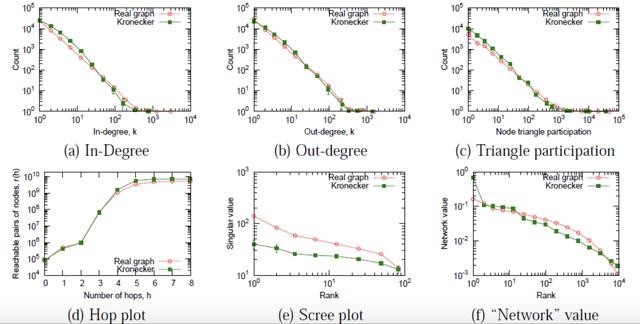
真实图和Kronecker图的指标非常接近: