在前三篇系列文章中,判定算法是基于图用邻接矩阵的表示,道路矩阵也是如此。事实上,因为邻接矩阵总是对称的,用一个上三角矩阵也可以表示。本文针对用上三角矩阵的表示法对原算法进行优化与实现。运算次数减少近一半。
1.源码:
1)优化的道路矩阵类头文件
#ifndef PATHARRAYOPTIMIZED_H
#define PATHARRAYOPTIMIZED_H
#include <iostream>
#include <vector>
using namespace std;
typedef vector<int> PATH;
typedef vector<PATH> PATHS;
typedef vector<vector<bool> > GRAPH_ADJ;
typedef vector<vector<PATH> > SINGLE_PATH_ARRAY;
typedef vector<vector<PATHS> > MULTI_PATHS_ARRAY;
class PathArrayOptimized
{
public:
PathArrayOptimized(const GRAPH_ADJ adjgraph);
PathArrayOptimized operator*(const PathArrayOptimized rc);
static vector<int> globalOffset;
private:
GRAPH_ADJ m_srcAdjArray;
SINGLE_PATH_ARRAY m_srcPathArray;
MULTI_PATHS_ARRAY m_multiPathsArray;
private:
void printAdjArray(const GRAPH_ADJ &adjArray);
void printPathArray(const SINGLE_PATH_ARRAY &pathArray);
void printPathsArray(const MULTI_PATHS_ARRAY &pathsArray);
PATH reversePath(PATH path);
public:
void adjArray2PathArray(const GRAPH_ADJ &srcAdjArray, SINGLE_PATH_ARRAY &dstPathArray);
void pathArray2PathsArray(const SINGLE_PATH_ARRAY &pathArray, MULTI_PATHS_ARRAY &pathsArray);
bool isZero();
void help();
PathArrayOptimized* clone() const { return new PathArrayOptimized( *this );}
};
#endif // PATHARRAYOPTIMIZED_H
2)优化的道路矩阵类实现文件
#include "patharrayoptimized.h"
vector<int> PathArrayOptimized::globalOffset = {0,1,2,3,4};
PathArrayOptimized::PathArrayOptimized(const GRAPH_ADJ adjgraph):
m_srcAdjArray(adjgraph)
{
adjArray2PathArray(m_srcAdjArray,m_srcPathArray);
pathArray2PathsArray(m_srcPathArray, m_multiPathsArray);
}
//print the source adjacency matrices to debug
void PathArrayOptimized::printAdjArray(const GRAPH_ADJ &adjArray)
{
if(adjArray.size() == 0)
{
cout << "Adjacency Array vector is null\n";
return;
}
int i = 0;
for (auto& line : adjArray) {
for (int j=0; j< i; j++) {
cout << " ";
}
for (const auto& v : line) {
cout << v << " ";
}
cout << endl;
i++;
}
}
//print the source path Array to debug
void PathArrayOptimized::printPathArray(const SINGLE_PATH_ARRAY &pathArray)
{
if(pathArray.size() == 0)
{
cout << "Path Array vector is null\n";
return;
}
int i = 0;
for (auto& line : pathArray) {
for (int j=0; j< i; j++) {
cout << " ";
}
for (const auto& path : line) {
if (path.size() == 1){
cout << "[0]";
continue;
}
cout << "[";
for (size_t i = 0; i < path.size(); ++i) {
cout << path[i];
if (i != path.size() - 1)
cout << "->";
}
cout << "] ";
}
cout << endl;
i++;
}
}
//print the source paths Array to debug
void PathArrayOptimized::printPathsArray(const MULTI_PATHS_ARRAY &pathsArray)
{
if(pathsArray.size() == 0)
{
cout << "Paths Array vector is null\n";
return;
}
int i = 0;
for (auto& line : pathsArray) {
for (int j=0; j< i; j++) {
cout << " ";
}
for (const auto& column : line) {
cout << "[";
for (const auto& path: column) {
if (path.size() == 1){
cout << "[0]";
continue;
}
cout << "[";
for (size_t i = 0; i < path.size(); ++i) {
cout << path[i];
if (i != path.size() - 1)
cout << "->";
}
cout << "]";
}
cout << "]";
}
cout << endl;
i++;
}
}
void PathArrayOptimized::help()
{
printPathsArray(m_multiPathsArray);
}
void PathArrayOptimized::adjArray2PathArray(const GRAPH_ADJ &srcAdjArray, SINGLE_PATH_ARRAY &dstPathArray)
{
dstPathArray.resize(srcAdjArray.size());
for (int i = 0; i < srcAdjArray.size(); ++i){
dstPathArray[i].resize(srcAdjArray[i].size());
}
for (int i = 0; i < srcAdjArray.size(); ++i){
for(int j= 0; j< srcAdjArray[i].size(); ++j)
{
if(srcAdjArray[i][j] == 0)
{
dstPathArray[i][j].push_back(0);
} else {
dstPathArray[i][j].push_back(i);
dstPathArray[i][j].push_back(j + globalOffset[i]);
}
}
}
}
void PathArrayOptimized::pathArray2PathsArray(const SINGLE_PATH_ARRAY &pathArray, MULTI_PATHS_ARRAY &pathsArray)
{
pathsArray.resize(pathArray.size());
for (int i = 0; i < pathArray.size(); ++i){
pathsArray[i].resize(pathArray[i].size());
}
for (int i = 0; i < pathArray.size(); ++i){
for(int j= 0; j< pathArray[i].size(); ++j)
{
pathsArray[i][j].resize(1);
pathsArray[i][j][0]=pathArray[i][j];
}
}
}
PathArrayOptimized PathArrayOptimized::operator*(const PathArrayOptimized pathArrayG)
{
PathArrayOptimized retgraph(pathArrayG.m_srcAdjArray);
retgraph.m_multiPathsArray.clear();
MULTI_PATHS_ARRAY retPathsArr;
//initialize the retPathArray
retPathsArr.resize(this->m_multiPathsArray.size());
for (int i=0; i < this->m_multiPathsArray.size(); ++i) {
retPathsArr[i].resize(this->m_multiPathsArray[i].size());
}
for (int i = 0; i < this->m_multiPathsArray.size(); ++i){
for(int j1= 0; j1< this->m_multiPathsArray[i].size(); ++j1)
{
int j = j1 + globalOffset[i];
PATHS retPaths;
for (int k=0; k < this->m_multiPathsArray.size(); ++k) {
//if one of path is [0], the result is 0
if (k<i) {
if((this->m_multiPathsArray[k][i-globalOffset[k]].size() == 1) && (this->m_multiPathsArray[k][i-globalOffset[k]][0].size() == 1))
{
continue;
}
} else {
if((this->m_multiPathsArray[i][k - globalOffset[i]].size() == 1) && (this->m_multiPathsArray[i][k - globalOffset[i]][0].size() == 1))
{
continue;
}
}
if (j<k) {
if((pathArrayG.m_multiPathsArray[j][k - globalOffset[j]].size() == 1) && (pathArrayG.m_multiPathsArray[j][k - globalOffset[j]][0].size() == 1))
{
continue;
}
} else {
if((pathArrayG.m_multiPathsArray[k][j - globalOffset[k]].size() == 1) && (pathArrayG.m_multiPathsArray[k][j - globalOffset[k]][0].size() == 1))
{
continue;
}
}
if(k< i) {
for (int x = 0; x < this->m_multiPathsArray[k][i - globalOffset[k]].size(); ++x){
if (j<k) {
for(int y= 0; y< pathArrayG.m_multiPathsArray[j][k - globalOffset[j]].size(); ++y)
{
PATH tempPath;
PATH inversePath1;
PATH inversePath2;
inversePath1 = reversePath(this->m_multiPathsArray[k][i-globalOffset[k]][x]);
inversePath2 = reversePath(pathArrayG.m_multiPathsArray[j][k-globalOffset[j]][y]);
PATH op1path = inversePath1;
PATH op2path = inversePath2;
bool bFlagCross = false;
int nCrossCount = 0;
if(op1path[op1path.size() -1] == op2path[0])
{
for (int m = 0; m < op1path.size() - 1; ++m) {
for (int n=0; n < op2path.size(); ++n) {
if (op1path[m] == op2path[n]){
bFlagCross = true;
nCrossCount ++;
}
}
}
if((op1path[0] == op2path[op2path.size() -1]) && (nCrossCount == 1))
{
if(this->m_multiPathsArray.size() == op1path.size() + op2path.size() - 2)
bFlagCross = false;
}
if( !bFlagCross ){
tempPath = op1path;
for(int n=1; n< op2path.size(); ++n)
{
tempPath.push_back(op2path[n]);
}
}
}
retPaths.push_back(tempPath);
}
} else {
for(int y= 0; y< pathArrayG.m_multiPathsArray[k][j-globalOffset[k]].size(); ++y)
{
PATH tempPath;
PATH inversePath1;
inversePath1 = reversePath(this->m_multiPathsArray[k][i-globalOffset[k]][x]);
PATH op1path = inversePath1;
PATH op2path = pathArrayG.m_multiPathsArray[k][j-globalOffset[k]][y];
bool bFlagCross = false;
int nCrossCount = 0;
if(op1path[op1path.size() -1] == op2path[0])
{
for (int m = 0; m < op1path.size() - 1; ++m) {
for (int n=0; n < op2path.size(); ++n) {
if (op1path[m] == op2path[n]){
bFlagCross = true;
nCrossCount ++;
}
}
}
if((op1path[0] == op2path[op2path.size() -1]) && (nCrossCount == 1))
{
if(this->m_multiPathsArray.size() == op1path.size() + op2path.size() - 2)
bFlagCross = false;
}
if( !bFlagCross ){
tempPath = op1path;
for(int n=1; n< op2path.size(); ++n)
{
tempPath.push_back(op2path[n]);
}
}
}
retPaths.push_back(tempPath);
}
}
}
} else {
for (int x = 0; x < this->m_multiPathsArray[i][k-globalOffset[i]].size(); ++x){
if (j<k) {
for(int y= 0; y< pathArrayG.m_multiPathsArray[j][k-globalOffset[j]].size(); ++y)
{
PATH tempPath;
PATH inversePath2;
inversePath2 = reversePath(pathArrayG.m_multiPathsArray[j][k-globalOffset[j]][y]);
PATH op1path = this->m_multiPathsArray[i][k-globalOffset[i]][x];
PATH op2path = inversePath2;
bool bFlagCross = false;
int nCrossCount = 0;
if(op1path[op1path.size() -1] == op2path[0])
{
for (int m = 0; m < op1path.size() - 1; ++m) {
for (int n=0; n < op2path.size(); ++n) {
if (op1path[m] == op2path[n]){
bFlagCross = true;
nCrossCount ++;
}
}
}
if((op1path[0] == op2path[op2path.size() -1]) && (nCrossCount == 1))
{
if(this->m_multiPathsArray.size() == op1path.size() + op2path.size() - 2)
bFlagCross = false;
}
if( !bFlagCross ){
tempPath = op1path;
for(int n=1; n< op2path.size(); ++n)
{
tempPath.push_back(op2path[n]);
}
}
}
retPaths.push_back(tempPath);
}
} else {
for(int y= 0; y< pathArrayG.m_multiPathsArray[k][j-globalOffset[k]].size(); ++y)
{
PATH tempPath;
PATH op1path = this->m_multiPathsArray[i][k-globalOffset[i]][x];
PATH op2path = pathArrayG.m_multiPathsArray[k][j-globalOffset[k]][y];
bool bFlagCross = false;
int nCrossCount = 0;
if(op1path[op1path.size() -1] == op2path[0])
{
for (int m = 0; m < op1path.size() - 1; ++m) {
for (int n=0; n < op2path.size(); ++n) {
if (op1path[m] == op2path[n]){
bFlagCross = true;
nCrossCount ++;
}
}
}
if((op1path[0] == op2path[op2path.size() -1]) && (nCrossCount == 1))
{
if(this->m_multiPathsArray.size() == op1path.size() + op2path.size() - 2)
bFlagCross = false;
}
if( !bFlagCross ){
tempPath = op1path;
for(int n=1; n< op2path.size(); ++n)
{
tempPath.push_back(op2path[n]);
}
}
}
retPaths.push_back(tempPath);
}
}
}
}
}
for (const auto& path: retPaths) {
if (path.size() !=0){
retPathsArr[i][j1].push_back(path);
}
}
//if the path is null, fill it with zero
if(retPathsArr[i][j1].size() == 0)
{
retPathsArr[i][j1].resize(1);
retPathsArr[i][j1][0].push_back(0);
}
}
}
retgraph.m_multiPathsArray.assign(retPathsArr.begin(),retPathsArr.end());
return retgraph;
}
PATH PathArrayOptimized::reversePath(PATH path){
PATH pathRet = path;
reverse(pathRet.begin(), pathRet.end());
return pathRet;
}
bool PathArrayOptimized::isZero()
{
bool bRet = true;
for (int i = 0; i < m_multiPathsArray.size(); ++i){
for(int j= 0; j< m_multiPathsArray[i].size(); ++j)
{
if (!((m_multiPathsArray[i][j].size() == 1) && (m_multiPathsArray[i][j][0][0] == 0)
|| (m_multiPathsArray[i][j].size() ==0)))
return false;
}
}
return bRet;
}
3)测试主程序
#include "patharrayoptimized.h"
using namespace std;
int main(int argc, char *argv[])
{
/*
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3)-------(4)
*/
vector<vector<bool>> graph = {
{0, 1, 0, 1, 0},
{0, 1, 1, 1},
{0, 0, 1},
{0, 1},
{0}
};
cout << "G1" << endl;
PathArrayOptimized G1(graph);
G1.help();
PathArrayOptimized G = G1;
for (int i=0; i<4; i++) {
G = G * G1;
cout << "G" << i+2 << endl;
G.help();
}
if(G.isZero()){
cout << "G does not have Hamilton circle\n";
} else {
cout << "G is Hamilton Graph with hamilton circle\n";
}
return 1;
}
2.执行结果:
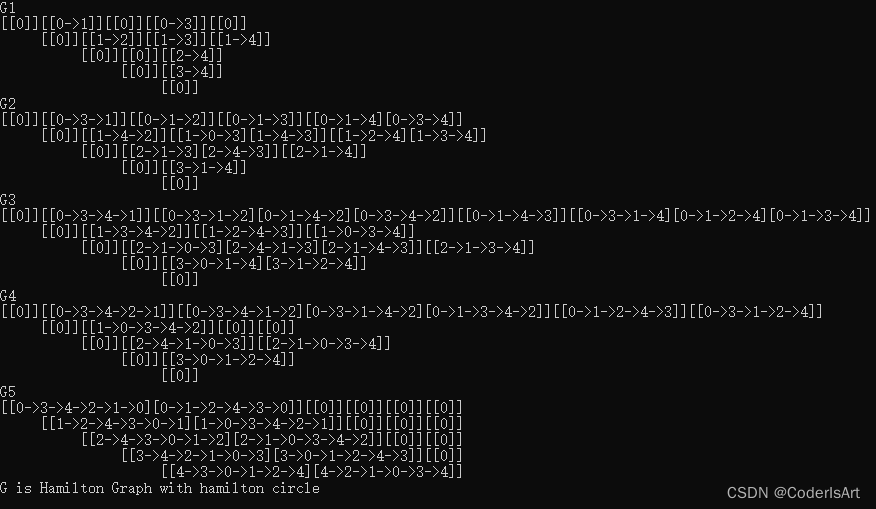
版权声明:本文为zkmrobot原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。