基础知识
文本相似度计算是把文本投影到向量空间,文本的相似度是把文本投影到向量空间,用向量相似度来表示语义相似度,通过比较计算向量的空间距离来比较文本的相似度。
Jaccard系数
Jaccard系数是计算两个集合重合度的常用方法:两个集合A和B交集元素的个数在A、B并集中所占的比例,称为这两个集合的Jaccard系数,用符号 J(A,B) 表示。Jaccard系数是衡量两个集合相似度的一种指标,公式如下:

其中,A,B集合中的元素为是文本中的全部词项,且集合中相同词项只保留一个。
余弦相似度
余弦相似度,是通过计算两个向量的夹角余弦值来评估向量间的相似度。将向量根据坐标映射到向量空间。求得他们的夹角,并得出夹角对应的余弦值,余弦值就可以用来表示这两个向量的相似性。
夹角越小,余弦值越接近于1,它们的方向更加吻合,则越相似。两个向量A,B之间的余弦相似度计算公式如下:
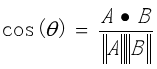
计算文本之间的余弦相似度时,首先要对文本分词、去除停用词,构建所有文本的词袋,然后计算文本词项的tf-idf值,接着利用词袋模型将每个文本都映射到统一的向量空间中,向量的坐标值就是对应的特征词项的tf-idf值。
实验内容
- 选定3个文本:doc1,doc2,doc3,其中doc1和doc2是两篇关于“机器学习”的介绍,doc3是1篇人大会议报道。
- 计算上述3个文档之间的Jaccard系数矩阵(行列为文档,元素值为两个文档之间的系数值)。
- 利用向量空间模型计算词项-文档关联矩阵,并计算3个文档之间余弦相似度矩阵(行列为文档,元素值为两个文档之间的相似度值)。
- 对比分析Jaccard系数和余弦相似度的性能。
步骤
- 获取停用词表,文本分词
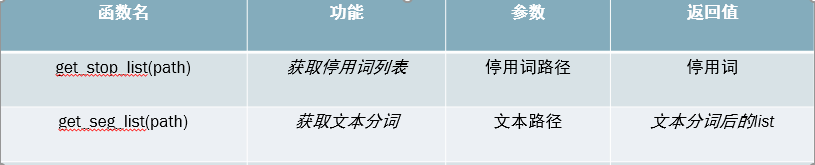
这一步是自然语言处理的基本操作,代码略。 - 获取去停用词后的词典

def get_dic(text_list, stop_words_list):
dic = {}
for myword in text_list:
if not (myword.strip() in stop_words_list):
dic.setdefault(myword, 0)
dic[myword] += 1
return dic
dic为该文本去除停用词之后的词典,键是文本中的词,值是这个词出现的频数
- 计算余弦相似度
首先,调用步骤1中的函数,清洗文本,获取全部词项
def get_cossimi_matrix(corpus_path, stop_path):
all = []
catelist = os.listdir(corpus_path)
stop_list = get_stop_list(stop_path)
for mydir in catelist:
print(' %s ' % mydir, end='')
text_path = corpus_path + '/' + mydir
samp_seg_list = get_seg_list(text_path) # 样例文本分词后的list
samp_str = ''
for word in samp_seg_list:
if word not in stop_list:
samp_str += word
samp_str += ' '
all.append(samp_str)
然后,计算每一个单词的tf-idf值,将文本用tf-idf矩阵表示,将文本映射到向量空间
vectorizer = CountVectorizer()
transformer = TfidfTransformer() # 统计每个词语的tf-idf权值函数
X = vectorizer.fit_transform(all) # 将文本转为词频矩阵
tfidf = transformer.fit_transform(X) # 计算tf-idf值
# 将tf-idf矩阵抽取出来,元素a[i][j]表示词项j在文本i中的tf-idf权重, 每一行表示一个文本在总的向量空间模型中映射的向量
tfidf_matrix = tfidf.toarray()
接着,编写计算余弦相似度函数
def get_cossimi(x, y):
myx = np.array(x)
myy = np.array(y)
cos1 = np.sum(myx * myy)
cos21 = np.sqrt(sum(myx * myx))
cos22 = np.sqrt(sum(myy * myy))
return cos1/float(cos21 * cos22)#return: 两个向量夹角的余弦值
传入参数为上一步求得的用tf-idf表示的文本,返回值是两个文本的余弦相似度。
最后,调用余弦相似度计算函数,按照列表循环的方式,分别比较三个文本的相似度
print('\n\t\tML_1\t\t\tML_2\t\t\trenda')
cossimi_matrix = [[0 for i in range(len(tfidf_matrix))] for i in range(len(tfidf_matrix))]
for i in range(0, len(tfidf_matrix)):#i元素为三个文本
print('text_%d\t' % (i + 1), end='')
for j in range(0, len(tfidf_matrix)):#j为被比较的文本,也是这三个文本,和i顺序相同。
cossimi_matrix[i][j] = get_cossimi(tfidf_matrix[i], tfidf_matrix[j])#计算余弦相似度
if i == j:
print("1.000000\t\t", end=' ')#如果i,j是同一篇文本,则余弦相似度为1
else:
print("%f\t\t"%get_cossimi(tfidf_matrix[i], tfidf_matrix[j]), end=' ')
采用嵌套循环的方式,两两比较文本相似度:
1)如果是同一篇文本,那么余弦值为1,输出余弦值
2)如果是不同文本,则调用余弦相似度计算函数,输出余弦值
因为本文语料是三篇文本,所以该程序一共输出3*3=9次。
- 计算Jaccard系数
首先,清洗文本,获取每篇文档的文本字典
fstop_seg_list = get_stop_list(stop_path)
dics = []
text_name = []
catelist = os.listdir(corpus_path)
for mydir in catelist:
text_path = corpus_path + '/'+ mydir
seg_list = get_seg_list(text_path) # 样例文本分词后的list
# 获取文本的去除停用词之后的字典
dics.append(get_dic(seg_list, fstop_seg_list))
text_name.append(mydir)
print(' %s '%mydir, end='')
这里,字典dics获取的是来自上文中统计好的去除停用词后的词典。
接着,编写计算jaccard系数函数
def get_jaccard(x, y):
all_words = {} # 大字典
all_words.update(x) # 用字典sample_words更新大字典
all_words.update(y) # 用字典mytest1_words更新大字典
xORy = len(all_words) #x和y并集中元素的个数
xANDy = 0 # x和y交集中元素的个数
for key in x.keys():
for key2 in y.keys():
if key == key2:
xANDy += 1
simi = float(xANDy)/xORy
return simi
在这个函数中,传入参数是用词典表示的文本,返回值是两个文本之间的Jaccard系数。
最后,采用嵌套循环的方式,两两计算Jaccard系数。
jaccard_matrix = [[0 for i in range(len(dics))] for i in range(len(dics))]
for i in range(0, len(dics)):
print('text_%d\t'%(i+1), end='')
for j in range(0, len(dics)):
jaccard_matrix[i][j] = get_jaccard(dics[i], dics[j])
print('%f\t\t'%get_jaccard(dics[i], dics[j]), end='')
print('\n')
return jaccard_matrix
结果及分析
实验结果如下:
余弦相似度矩阵为:

text_1和ML_1,text_2和ML_2,text_3和renda为同一篇文档。
两篇机器学习文档的相似度为:0.146312
机器学习文档与人大会议文档的相似度为:0.004487,0.014308.
可以看出,两篇相同主题的文档相似度较高,且远远高于不同主题的文档。
Jaccard系数矩阵为:

两篇机器学习文档的相似度为:0.091429
机器学习文档与人大会议文档的相似度为:0.009019,0.009231.
对比余弦相似度矩阵,综合来看,余弦相似度较jaccard系数在衡量文本相似度时区分度更高,效果更明显。
分析:
这是由于mjaccard系数在计算时,不考虑词项在文档中出现的次数,也不考虑罕见词可能带来更大的信息量这个问题。而向量空间模型兼顾到了这两点,因而余弦相似度取得了更好的效果。