目录
重排链表
链表1
L2-022 重排链表 (25 分)
给定一个单链表 L1→L2→⋯→Ln−1→Ln,请编写程序将链表重新排列为 Ln→L1→Ln−1→L2→⋯。例如:给定L为1→2→3→4→5→6,则输出应该为6→1→5→2→4→3。
输入格式:
每个输入包含1个测试用例。每个测试用例第1行给出第1个结点的地址和结点总个数,即正整数N (≤105)。结点的地址是5位非负整数,NULL地址用−1表示。
接下来有N行,每行格式为:
Address Data Next
其中Address是结点地址;Data是该结点保存的数据,为不超过105的正整数;Next是下一结点的地址。题目保证给出的链表上至少有两个结点。
输出格式:
对每个测试用例,顺序输出重排后的结果链表,其上每个结点占一行,格式与输入相同。
输入样例:
00100 6
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218
输出样例:
68237 6 00100
00100 1 99999
99999 5 12309
12309 2 00000
00000 4 33218
33218 3 -1思路:根据地址,先将各个节点串起来。(在串起来的过程中,分配个权重,用来排序,这样就可以避免链表,直接使用数组来操作)
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
struct node{
int address,value,next;
int id;
}a[N];
bool cmp(node a,node b){
return a.id<b.id;
}
int main(){
for(int i = 0;i<=N-1;++i)a[i].id = INT_MAX;
int head,n;scanf("%d %d",&head,&n);
for(int i = 1;i<=n;++i){
int address,value,next;scanf("%d %d %d",&address,&value,&next);
a[address].address=address;
a[address].value = value;
a[address].next = next;
}
int id= 0;
while(head!=-1){
a[head].id = id++;
head = a[head].next;
}
id--;
sort(a,a+N,cmp);
//for(int i = 0;i<=id;++i)cout<<a[i].value<<endl;
int i=0,j=id;
while(i<=j){
if(i==j)printf("%05d %d -1\n",a[j].address,a[j].value),j--;
else printf("%05d %d %05d\n",a[j].address,a[j].value,a[i].address),j--;
if(i>j)break;
if(i==j)printf("%05d %d -1\n",a[i].address,a[i].value),i++;
else printf("%05d %d %05d\n",a[i].address,a[i].value,a[j].address),i++;
}
return 0;
} 链表2
给定一个单链表 L,我们将每 K 个结点看成一个区块(链表最后若不足 K 个结点,也看成一个区块),请编写程序将 L 中所有区块的链接反转。例如:给定 L 为 1→2→3→4→5→6→7→8,K 为 3,则输出应该为 7→8→4→5→6→1→2→3。
思路:只是排序的标准不一样了,先分块,再分在每一块里具体的下标
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
struct node{
int address,value,next;
int tag1,tag2;
}a[N];
bool cmp(const node a,const node b){
if(a.tag1!=b.tag1)return a.tag1>b.tag1;
return a.tag2<b.tag2;
}
int main(){
int head,n,k;;
while(~scanf("%d %d %d",&head,&n,&k)){
for(int i = 0;i<=N-1;++i)a[i].tag1=a[i].tag2=-1;
for(int i = 1;i<=n;++i){
int address,value,next;scanf("%d %d %d",&address,&value,&next);
a[address].address=address;
a[address].value = value;
a[address].next = next;
}
int id= 0;
while(head!=-1){
a[head].tag1 = id/k;
a[head].tag2 = id%k;
head = a[head].next;
++id;
}
id--;
sort(a,a+N,cmp);
int i=0,j=id;
while(i<=j){
if(i==j)printf("%05d %d -1\n",a[i].address,a[i].value);
else printf("%05d %d %05d\n",a[i].address,a[i].value,a[i+1].address);
++i;
}
}
return 0;
} 部落
在一个社区里,每个人都有自己的小圈子,还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里,于是要请你统计一下,在一个给定社区中,到底有多少个互不相交的部落?并且检查任意两个人是否属于同一个部落。
输入格式:
输入在第一行给出一个正整数N(≤1e4),是已知小圈子的个数。随后N行,每行按下列格式给出一个小圈子里的人:
K P[1] P[2] ⋯ P[K]
其中K是小圈子里的人数,P[i](i=1,⋯,K)是小圈子里每个人的编号。这里所有人的编号从1开始连续编号,最大编号不会超过1e4。
之后一行给出一个非负整数Q(≤1e4),是查询次数。随后Q行,每行给出一对被查询的人的编号。
输出格式:
首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询,如果他们属于同一个部落,则在一行中输出Y,否则输出N。
输入样例:
4
3 10 1 2
2 3 4
4 1 5 7 8
3 9 6 4
2
10 5
3 7
输出样例:
10 2
Y
N#include<bits/stdc++.h>
using namespace std;
int n;
const int N = 1e4+5;
int root[N];
void init(){
for(int i = 1;i<=N-1;++i)root[i]=i;
}
int Find(int x){
if(x!=root[x])root[x]=Find(root[x]);
return root[x];
}
set<int>ss;
set<int>e;
int main(){
init();
scanf("%d",&n);
for(int i = 1;i<=n;++i){
int k;scanf("%d",&k);
int basic;scanf("%d",&basic);ss.insert(basic);
int fx = Find(basic);
for(int j=2;j<=k;++j){
int x;scanf("%d",&x);ss.insert(x);
int fy = Find(x);
if(fx!=fy)root[fy] = fx; //fx相当于是一个小部落中的源 root[fx] = fy 这样就有问题
}
}
printf("%d ",ss.size());
set<int>::iterator it = ss.begin();
for(;it!=ss.end();++it){
e.insert(Find(*it));
}
printf("%d\n",e.size());
int q;scanf("%d",&q);
while(q--){
int x,y;scanf("%d %d",&x,&y);
int fx = Find(x),fy = Find(y);
if(fx!=fy)printf("N\n");
else printf("Y\n");
}
return 0;
} 分而治之
分而治之,各个击破是兵家常用的策略之一。在战争中,我们希望首先攻下敌方的部分城市,使其剩余的城市变成孤立无援,然后再分头各个击破。为此参谋部提供了若干打击方案。本题就请你编写程序,判断每个方案的可行性。
输入格式:
输入在第一行给出两个正整数 N 和 M(均不超过10 000),分别为敌方城市个数(于是默认城市从 1 到 N 编号)和连接两城市的通路条数。随后 M 行,每行给出一条通路所连接的两个城市的编号,其间以一个空格分隔。在城市信息之后给出参谋部的系列方案,即一个正整数 K (≤ 100)和随后的 K 行方案,每行按以下格式给出:
Np v[1] v[2] ... v[Np]
其中 Np 是该方案中计划攻下的城市数量,后面的系列 v[i] 是计划攻下的城市编号。
输出格式:
对每一套方案,如果可行就输出YES,否则输出NO。
输入样例:
10 11
8 7
6 8
4 5
8 4
8 1
1 2
1 4
9 8
9 1
1 10
2 4
5
4 10 3 8 4
6 6 1 7 5 4 9
3 1 8 4
2 2 8
7 9 8 7 6 5 4 2
输出样例:
NO
YES
YES
NO
NO 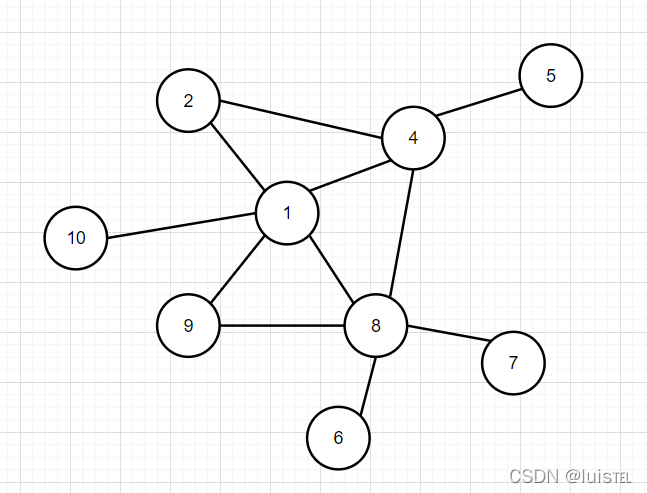
思路:先统计出每个点的度是多少,记为a[i]。之后输入每个攻占的点的时候,将这个点邻接的点的度数都减1,千万记得,被攻占的点度数要直接赋值为0! 最后再遍历一遍a[i]数组,如果有节点的度数是大于0的,那就说明还有连接在一起的节点。a[i]在遍历之后,可能为负值。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
vector<int>v[N];
int a[N]; // 记录各节点的度
int main(){
int n,m;scanf("%d %d",&n,&m);
while(m--){
int x,y;scanf("%d %d",&x,&y);
v[x].push_back(y),v[y].push_back(x);
}
int k;scanf("%d",&k);
while(k--){
for(int i = 1;i<=n;++i)a[i]=v[i].size();
int np;scanf("%d",&np);
while(np--){
int x;scanf("%d",&x);a[x] = 0; // 一定要把去除的这个点的度置0,当时找错误找死了
for(int j = 0;j<v[x].size();++j)a[v[x][j]]--;
}
int sign = 0;
for(int i = 1;i<=n;++i){
if(a[i]>0){
printf("NO\n");
sign = 1;
break;
}
}
if(!sign)printf("YES\n");
}
return 0;
} 完全二叉树的层序遍历
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是完美二叉树。对于深度为 D 的,有 N 个结点的二叉树,若其结点对应于相同深度完美二叉树的层序遍历的前 N 个结点,这样的树就是完全二叉树。
给定一棵完全二叉树的后序遍历,请你给出这棵树的层序遍历结果。
输入格式:
输入在第一行中给出正整数 N(≤30),即树中结点个数。第二行给出后序遍历序列,为 N 个不超过 100 的正整数。同一行中所有数字都以空格分隔。
输出格式:
在一行中输出该树的层序遍历序列。所有数字都以 1 个空格分隔,行首尾不得有多余空格。
输入样例:
8
91 71 2 34 10 15 55 18
输出样例:
18 34 55 71 2 10 15 91是完全二叉树,不是满二叉树,所以节点8个是可以的。当时还在想,完全二叉树节点数不应该是 1 3 7 15 吗….
#include<bits/stdc++.h>
using namespace std;
int n,tree[105];
void create(int i) {
if(i>n) return ;
create(2*i);
create(2*i+1);
scanf("%d",&tree[i]);
}
int main() {
scanf("%d",&n);
create(1);
for(int i=1;i<=n;i++) {
if(i>1)putchar(' ');
printf("%d",tree[i]);
}
return 0;
}病毒溯源
现给定一些病毒之间的变异关系,要求你找出其中最长的一条变异链。
在此假设给出的变异都是由突变引起的,不考虑复杂的基因重组变异问题 —— 即每一种病毒都是由唯一的一种病毒突变而来,并且不存在循环变异的情况。
输入格式:
输入在第一行中给出一个正整数 N(≤1e4),即病毒种类的总数。于是我们将所有病毒从 0 到 N−1 进行编号。
随后 N 行,每行按以下格式描述一种病毒的变异情况:
k 变异株1 …… 变异株k
其中 k 是该病毒产生的变异毒株的种类数,后面跟着每种变异株的编号。第 i 行对应编号为 i 的病毒(0≤i<N)。题目保证病毒源头有且仅有一个。
输出格式:
首先输出从源头开始最长变异链的长度。
在第二行中输出从源头开始最长的一条变异链,编号间以 1 个空格分隔,行首尾不得有多余空格。如果最长链不唯一,则输出最小序列。
注:我们称序列 { a1,⋯,an } 比序列 { b1,⋯,bn } “小”,如果存在 1≤k≤n 满足 ai=bi 对所有 i<k 成立,且 ak<bk。
输入样例:
10
3 6 4 8
0
0
0
2 5 9
0
1 7
1 2
0
2 3 1
输出样例:
4
0 4 9 1 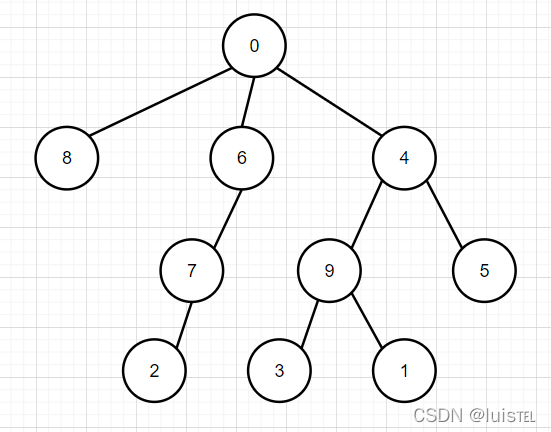
思路:先将每个节点的子节点按编号从大到小排序,方便输出最小序列。只要后面出现层数相同的链,就可以直接替换。
坑点: 0不一定是病毒的源头。该怎么找到源头?在所有的子节点中没有出现的编号就是源头。
#include<bits/stdc++.h>
using namespace std;
const int N = 1E5+5;
int temp[N];
vector<int>v[N];
int depth = 0;
int a[N];
// pos : 病毒的编号 layer: 搜索的层数
void dfs(int pos,int layer){
if(v[pos].size()==0){
if(layer-1>=depth){
for(int i = 1;i<=layer-1;++i)a[i] = temp[i];
depth = layer-1;
}
}
for(int i = 0;i<v[pos].size();++i){
temp[layer] = v[pos][i];
dfs(v[pos][i],layer+1);
}
}
int sign[N]; //标记病源
int main(){
int n;scanf("%d",&n);
for(int i = 0;i<n;++i){
int k;scanf("%d",&k);
int x;
for(int j = 1;j<=k;++j)scanf("%d",&x),v[i].push_back(x),sign[x]=1;
sort(v[i].begin(),v[i].end(),greater<int>());
}
// pos 病毒的编号
int pos = -1;
for(int i = 0;i<n;++i){
if(!sign[i]){
pos = i;
break;
}
}
dfs(pos,1);
printf("%d\n%d",depth+1,pos);
for(int i = 1;i<=depth;++i)printf(" %d",a[i]);
putchar(10);
return 0;
} L2-039 清点代码库
输入样例:
7 3
35 28 74
-1 -1 22
28 74 35
-1 -1 22
11 66 0
35 28 74
35 28 74
输出样例:
4
3 35 28 74
2 -1 -1 22
1 11 66 0
1 28 74 35思路:对数组之间进行排序。此前都只是对一个数组之内的元素进行排序。首次接触数组之间的排序
#include<bits/stdc++.h>
using namespace std;
int n,m,x;
#define ll long long
map<vector<int>,int>mp; // dev里, pair的vector要放在int前, 不懂呀...
vector<pair<vector<int>,int> >v;
bool cmp(pair<vector<int>,int> a,pair<vector<int>,int> b){
if(a.second!=b.second)return a.second>b.second;
else{ // 实现对数组之间进行排序
for(int i = 0;i<m;++i){
if(a.first[i]!=b.first[i])return a.first[i]<b.first[i];
}
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 1;i<=n;++i){
vector<int>_; //如果想要并列写,就要注意用逗号分隔,不是分号
for(int j = 1;j<=m;++j)scanf("%d",&x),_.push_back(x);
mp[_]++;
}
map<vector<int>,int>::iterator it = mp.begin();
for(;it!=mp.end();++it)v.push_back({it->first,it->second});
sort(v.begin(),v.end(),cmp);
printf("%d\n",mp.size());
for(int i = 0;i<v.size();++i){
printf("%d",v[i].second);
for(int j = 0;j<v[i].first.size();++j)printf(" %d",v[i].first[j]);
putchar(10);
}
return 0;
} 倍数问题
题目描述
众所周知,小葱同学擅长计算,尤其擅长计算一个数是否是另外一个数的倍数。
但小葱只擅长两个数的情况,当有很多个数之后就会比较苦恼。
现在小葱给了你 n 个数,希望你从这 n 个数中找到三个数
使得这三个数的和是 K 的倍数,且这个和最大。数据保证一定有解。输入
第一行包括 2 个正整数 n, K。
第二行 n 个正整数,代表给定的 n 个数。
1 <= n <= 10^5, 1 <= K <= 10^3,给定的 n 个数均不超过 10^8。输出
输出一行一个整数代表所求的和。
样例输入
4 3 1 2 3 4样例输出
9
其实是个背包问题,但我还不太会。
关键点:
设模为 m ,要加入的数为 x
那么, 再加入余数为 m – x%m 的数,那么和的余数就为0了。
如果想余数为k,那就在后面加k好了, 即 ( m – x%m + k ) % m 注意再取模一下。因为加了一个k,前面那一部分的和就大于 m 了。
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int n,m;
vector<int>a[N];
int f[4][N];
int main(){
while(~scanf("%d %d",&n,&m)){
for(int i = 0;i<=m;++i)a[i].clear();
for(int i = 1;i<=n;++i){
int x;scanf("%d",&x);
a[x%m].push_back(x);
}
memset(f,-9999,sizeof(f));
f[0][0] = 0;
for(int i = 0;i<m;++i){
sort(a[i].begin(),a[i].end(),greater<int>());
for(int u = 0;u<3&&a[i].size()>u;++u){ //每个余数最多只取3个,因为最多就取3个
int x = a[i][u]; // 准备要放进背包的数
for(int j = 3;j>=1;--j){
for(int k = 0;k<m;++k){
// f[j][k] : 选j个数,和的余数为 k
f[j][k] = max(f[j][k],f[j-1][(m-x%m+k)%m]+x);
// 注意取模 (m-x%m+k)%m 加k后,要再去模
// m-x%m 放进余数为这个数的数,那和的余数就为0了,
// 如果想余数为k,在后面直接加 k 就好了
}
}
}
}
printf("%d\n",f[3][0]); // 选3个数,余数为0
}
return 0;
}接雨水
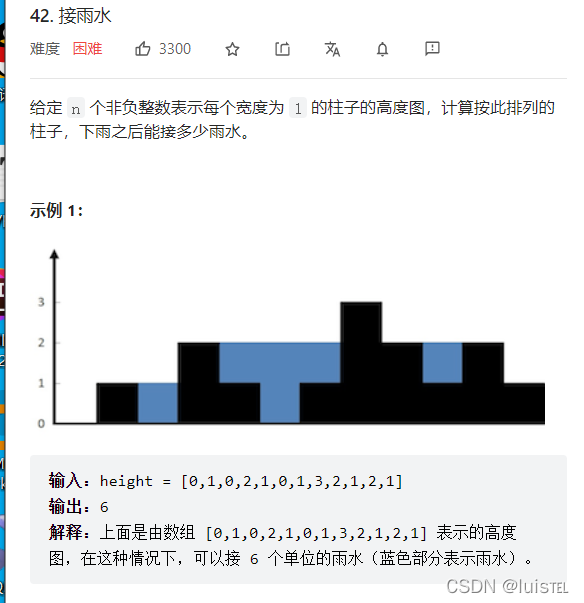
分析:这题算是一题逻辑题吧!只要想通了就很好理解。没做过这种题型,想的话,可能会的比较久,或者想偏吧。
对于某一个位置,算出左边的最高和右边的最高,两者再取最小值(短板效应),再减去自身的高度,得到的就是这个位置能够接到水的高度!
class Solution {
public:
int f[20005],v[20005];// 存放i位置的 左边的最大值和右边的最大值
int trap(vector<int>& height) {
int n = height.size();
f[0] = 0;
for(int i = 1;i<=n;++i){
f[i] = max(f[i-1],height[i-1]);
}
v[n+1] = 0;
for(int i = n;i;--i){
v[i] = max(v[i+1],height[i-1]);
}
int ans = 0;
for(int i = 1;i<=n;++i){
ans += min(f[i],v[i]) - height[i-1];
}
return ans;
}
};模型抽象
求逆序数
P1908 逆序对 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P1908解法1:归并排序
https://www.luogu.com.cn/problem/P1908解法1:归并排序
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n;
#define ll long long
int a[N];
int temp[N];
ll ans = 0;
void merge_sort(int l,int r){
if(l == r)return;
int mid = (l+r)>>1;
merge_sort(l,mid);
merge_sort(mid+1,r);
int i = l, j = mid+1, k = l;
while(i<=mid&&j<=r){
if(a[i]<=a[j])temp[k++] = a[i++];
else temp[k++] = a[j++],ans += mid - i + 1; // 与归并排序的模板就多了这一行
}
while(i<=mid)temp[k++] = a[i++];
while(j<=r)temp[k++] = a[j++];
for(int i = l;i<=r;++i)a[i] = temp[i];
}
int main(){
scanf("%d",&n);
for(int i = 1;i<=n;++i)scanf("%d",&a[i]);
merge_sort(1,n);
printf("%lld\n",ans);
return 0;
}解法2:数组数组 + 离散化
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n;
#define ll long long
struct node{
int v;
int index;
}a[N];
int tree[N];
int lowbit(int x){
return x&-x;
}
void add(int x){
while(x<=n){
tree[x]++; // 相当于新增一个数 ,所以是加1操作,就不用多传一个参数k了
x += lowbit(x);
}
}
int query(int x){
int ans = 0;
while(x){
ans += tree[x];
x -= lowbit(x);
}
return ans;
}
bool cmp(const node&a,const node&b){
return a.v<b.v;
}
int main(){
scanf("%d",&n);
for(int i = 1;i<=n;++i){
scanf("%d",&a[i].v);
a[i].index = i;
}
// 要保证两个数相等时,相对下标是不变的
stable_sort(a+1,a+1+n,cmp);
ll ans = 0;
for(int i = 1;i<=n;++i){
add(a[i].index);
ans += i - query(a[i].index);
}
cout<<ans<<endl;
return 0;
}278. 数字组合 – AcWing题库![]() https://www.acwing.com/problem/content/280/
https://www.acwing.com/problem/content/280/
可以抽象成n个物品,背包体积为M的 01背包问题。
#include<bits/stdc++.h>
using namespace std;
int dp[10005];
int a[105];
int main(){
int n,m;scanf("%d %d",&n,&m);
for(int i = 1;i<=n;++i)scanf("%d",&a[i]);
dp[0] = 1;
for(int i = 1;i<=n;++i){
for(int j = m;j>=a[i];--j){
dp[j] += dp[j-a[i]];
}
}
printf("%d\n",dp[m]);
return 0;
}
279. 自然数拆分 – AcWing题库![]() https://www.acwing.com/problem/content/281/
https://www.acwing.com/problem/content/281/

这题其实是跟数的划分是一样的,不过我之前的代码是这样的:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n;
int f[1005][1005];
int main() {
while(~scanf("%d",&n)){
memset(f,0,sizeof(f));
f[0][0] = 1; // 0分成0份也是一种分法
// f[i][j] 把 i 划分成 j 份的分法
for(int i = 1;i<=n;++i){
for(int j = 1;j<=i;++j){
f[i][j] = f[i-1][j-1]+f[i-j][j];
}
}
int ans = 0;
for(int i = 1;i<=n;++i)ans += f[n][i];
printf("%d\n",ans);
}
return 0;
}如果数据大一点,再使用long long,那么使用二维数组就会内存超限。
其实这题,可以抽象为完全背包问题,把一个数划分成其他数,也就是 由其他数去组成一个数。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll f[4005];
const ll mod = 2147483648;
int main(){
int n;scanf("%d",&n);
f[0] = 1;
for(int i = 1;i<n;++i){ // 限制至少由两个数组成
for(int j = i;j<=n;++j){
f[j] = (f[j] + f[j- i])%mod;
}
}
printf("%lld\n",f[n]);
return 0;
}