视觉SLAM总结-前端视觉里程计-特征点法

一、2D-2D相机位姿估计

2D-2D相机位姿估计通常利用 对极几何 进行计算，是单目SLAM初始化时的关键技术。

2D-2D 对极几何主要涉及到基础矩阵、本质矩阵和单应性矩阵的求解，并从中恢复出旋转矩阵 R 和平移向量 t，参考基础矩阵F和本质矩阵E 单应矩阵H计算，然后三角化一些点，参考三角形法

注意事项：

1.使用条件

计算基础矩阵或本质矩阵适用于特征点不共面的情况，计算单应矩阵适用于特征点共面的情况

2.退化.

当特征点共面或者相机发生纯旋转时，基础矩阵 F的自由度下降，就会出现所谓的退化(degenerate)。为了能够避免退化现象的影响，通常会同时估计基础矩阵 F和单应矩阵 H，选择重投影误差比较小的那个作为最终的运动估计矩阵。

3. 尺度不确定性

尺度不确定性，用上面的方法估计出的相机平移向量t的值并没有单位，也就是说相机移动的距离只有相对值，没有绝对值。这是单目相机固有的尺度不确定性问题，无法从根本上解决。因此单目SLAM中一般把初始化后的t归一化，即把初始化时移动的距离默认为1，此后的距离都以这个1为单位。

4.初始化问题

初始化的纯旋转问题：单目初始化不能只有旋转，必须要有一定程度的平移，否则由于t趋近于0，导致无从求解R或者误差非常大

5.多于8对点：RANSAC

如果匹配的点对数多于8（大多数情况都是这样），可以考虑充分利用这些点，而不是只从中选择8对用于计算。推荐的算法是随机采样一致性（Random Sample Consensus，RANSAC），该算法可以有效地避免错误数据对整体结果的影响。在代码中，只需要将findFundamentalMat函数的第三个参数从CV_FM_8POINT换成CV_FM_RANSAC就可以了。

Ref: 2D-2D相机位姿估计计算机视觉对极几何之FEH

opencv函数实现2D-2D相机姿态估计

void pose_estimation_2d2d ( std::vector<KeyPoint> keypoints_1,
                            std::vector<KeyPoint> keypoints_2,
                            std::vector< DMatch > matches,
                            Mat& R, Mat& t )
{
    // 相机内参,TUM Freiburg2
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );

    //-- 把匹配点转换为vector<Point2f>的形式
    vector<Point2f> points1;
    vector<Point2f> points2;

    for ( int i = 0; i < ( int ) matches.size(); i++ )
    {
        points1.push_back ( keypoints_1[matches[i].queryIdx].pt );
        points2.push_back ( keypoints_2[matches[i].trainIdx].pt );
    }

    //-- 计算基础矩阵
    Mat fundamental_matrix;
    fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
    cout<<"fundamental_matrix is "<<endl<< fundamental_matrix<<endl;

    //-- 计算本质矩阵
    Point2d principal_point ( 325.1, 249.7 );	//相机光心, TUM dataset标定值
    double focal_length = 521;			//相机焦距, TUM dataset标定值
    Mat essential_matrix;
    essential_matrix = findEssentialMat ( points1, points2, focal_length, principal_point );
    cout<<"essential_matrix is "<<endl<< essential_matrix<<endl;

    //-- 计算单应矩阵
    Mat homography_matrix;
    homography_matrix = findHomography ( points1, points2, RANSAC, 3 );
    cout<<"homography_matrix is "<<endl<<homography_matrix<<endl;

    //-- 从本质矩阵中恢复旋转和平移信息.
    recoverPose ( essential_matrix, points1, points2, R, t, focal_length, principal_point );
    cout<<"R is "<<endl<<R<<endl;
    cout<<"t is "<<endl<<t<<endl;
    
}

二、3D-2D相机位姿估计

PnP(Perspective-n-Point) 是求解3D到2D点对运动的方法，它描述了当知道n个空间点及其投影位置时，如何估计相机的姿态。求解PnP问题目前主要有直接线性变换（DLT）、P3P、EPnP、UPnP以及非线性优化方法。维基百科Perspective-n-Point（Wikipedia）

1.直线线性变换法DLT

考虑某个空间点，坐标为 $P(X,Y,Z,1)^{T}$ ,图像I1中，投影到特征点 $x1=(u1,v1,1)^{T}$ (归一化平面平面的坐标)，此时的相机位姿为R，t是未知的。写T=【R,t】

T的行向量为t1,t2,t3 ,化简得

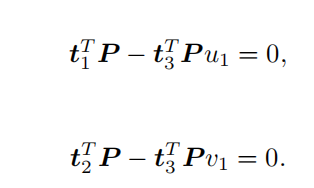
一对匹配点得到2对，T有12个元素，至少需要6对点匹配，对于大于6点可采用SVD进行超定方程的求解

注意：需要对左边的3*3的矩阵块用一个最好的旋转矩阵来近似，可以用QR分解完成。

2. 三对点匹配P3P算法

P3P原理示意图：

以上的图，OA,OB,OC是未知量。x=OA/OC,y=OB/OC，用余弦定理得到：

把等式右侧的三项设为v，u*v，w*v，v=AB2/OC2，u=BC2/AB2，w=AC2/AB2是已知的，cos都已知，那么目前是x，y不知道，v不知道。把第一个式子代入后俩，消去v，式子变成：

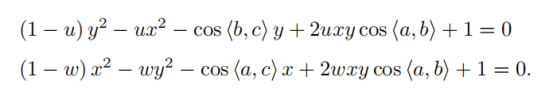
求出x，y以后，代入第上面三个式子中的第一个，可以求出v，v是AB2/OC2，就可以求出OC

注意事项：

1.cos值:2D点图像位置已知，光心位置已知，可以计算其夹角，进而计算余弦。

2.P3P只利用了3点的信息，当给的匹配点多于3个得时候。难于利用更多的信息

3.如果3D或2D点的受噪声的影响，或者出现无匹配时，则算法失效

4.相机坐标系下3D坐标已知，可以据此求解3D-3D的ICP问题。

opencv函数设计函数：

solvePnP
Rodrigues

    vector<KeyPoint> keypoints_1, keypoints_2;
    vector<DMatch> matches;
    find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
    cout<<"一共找到了"<<matches.size() <<"组匹配点"<<endl;

    // 建立3D点
    Mat d1 = imread ( argv[3], CV_LOAD_IMAGE_UNCHANGED );       // 深度图为16位无符号数，单通道图像
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector<Point3f> pts_3d;
    vector<Point2f> pts_2d;
    for ( DMatch m:matches )
    {
        ushort d = d1.ptr<unsigned short> (int ( keypoints_1[m.queryIdx].pt.y )) [ int ( keypoints_1[m.queryIdx].pt.x ) ];
        if ( d == 0 )   // bad depth
            continue;
        float dd = d/5000.0;
        Point2d p1 = pixel2cam ( keypoints_1[m.queryIdx].pt, K );
        pts_3d.push_back ( Point3f ( p1.x*dd, p1.y*dd, dd ) );
        pts_2d.push_back ( keypoints_2[m.trainIdx].pt );
    }

    cout<<"3d-2d pairs: "<<pts_3d.size() <<endl;

    Mat r, t;
    solvePnP ( pts_3d, pts_2d, K, Mat(), r, t, false ); // 调用OpenCV 的 PnP 求解，可选 
  择EPNP，DLS等方法
    Mat R;
    cv::Rodrigues ( r, R ); // r为旋转向量形式，用Rodrigues公式转换为矩阵

    cout<<"R="<<endl<<R<<endl;
    cout<<"t="<<endl<<t<<endl;

    cout<<"calling bundle adjustment"<<endl;

3.非线性优化BA

在双目或RGB-D的视觉里程计中，可以直接使用PnP估计相机运动；而在单目视觉里程计中，必须先进行初始化，然后才能使用PnP。在SLAM中，通常先使用 P3P或EPnP 等方法估计相机位姿，再构建最小二乘优化问题对估计值进行调整（BA）。

把 PnP问题构建成一个定义于李代数上的非线性最小二乘问题，求解最好的相机位姿。

定义残差（观测值-预测值）或重投影误差

构建最小二乘问题:

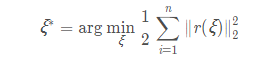
采用的g2o库优化工具：

void bundleAdjustment (
    const vector< Point3f > points_3d,
    const vector< Point2f > points_2d,
    const Mat& K,
    Mat& R, Mat& t )
{
    // 初始化g2o
    typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>(); // 线性方程求解器
    Block* solver_ptr = new Block ( linearSolver );     // 矩阵块求解器
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm ( solver );

    // vertex
    g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
    Eigen::Matrix3d R_mat;
    R_mat <<
          R.at<double> ( 0,0 ), R.at<double> ( 0,1 ), R.at<double> ( 0,2 ),
               R.at<double> ( 1,0 ), R.at<double> ( 1,1 ), R.at<double> ( 1,2 ),
               R.at<double> ( 2,0 ), R.at<double> ( 2,1 ), R.at<double> ( 2,2 );
    pose->setId ( 0 );
    pose->setEstimate ( g2o::SE3Quat (
                            R_mat,
                            Eigen::Vector3d ( t.at<double> ( 0,0 ), t.at<double> ( 1,0 ), t.at<double> ( 2,0 ) )
                        ) );
    optimizer.addVertex ( pose );

    int index = 1;
    for ( const Point3f p:points_3d )   // landmarks
    {
        g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
        point->setId ( index++ );
        point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
        point->setMarginalized ( true ); // g2o 中必须设置 marg 参见第十讲内容
        optimizer.addVertex ( point );
    }

    // parameter: camera intrinsics
    g2o::CameraParameters* camera = new g2o::CameraParameters (
        K.at<double> ( 0,0 ), Eigen::Vector2d ( K.at<double> ( 0,2 ), K.at<double> ( 1,2 ) ), 0
    );
    camera->setId ( 0 );
    optimizer.addParameter ( camera );

    // edges
    index = 1;
    for ( const Point2f p:points_2d )
    {
        g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
        edge->setId ( index );
        edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
        edge->setVertex ( 1, pose );
        edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
        edge->setParameterId ( 0,0 );
        edge->setInformation ( Eigen::Matrix2d::Identity() );
        optimizer.addEdge ( edge );
        index++;
    }

    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    optimizer.setVerbose ( true );
    optimizer.initializeOptimization();
    optimizer.optimize ( 100 );
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>> ( t2-t1 );
    cout<<"optimization costs time: "<<time_used.count() <<" seconds."<<endl;

    cout<<endl<<"after optimization:"<<endl;
    cout<<"T="<<endl<<Eigen::Isometry3d ( pose->estimate() ).matrix() <<endl;
}

ref 视觉SLAM位姿估计

三、3D-3D相机位姿估计

3D-2D相机位姿估计，采用PnP方法估计单目SLAM的相机位姿。而对于RGBD深度相机来说，每张图片都有深度信息，如果还用PnP方法，就无法充分利用已知的信息。本部分将介绍专门用于3D-3D相机位姿估计的方法。

两组3D点中恢复出相机位姿信息的方法通常称为迭代最近点（Iterative Closest Point，ICP）。和PnP类似，ICP的求解也分为两种方式：利用线性代数求解（SVD方法）以及利用非线性优化方式求解（类似于Bundle Adjustment）

1.SVD线性求解

推导：

代码：

void pose_estimation_3d3d (
    const vector<Point3f>& pts1,
    const vector<Point3f>& pts2,
    Mat& R, Mat& t
)
{
    Point3f p1, p2;     // center of mass
    int N = pts1.size();
    for ( int i=0; i<N; i++ )
    {
        p1 += pts1[i];
        p2 += pts2[i];
    }
    p1 = Point3f( Vec3f(p1) /  N);
    p2 = Point3f( Vec3f(p2) / N);
    vector<Point3f>     q1 ( N ), q2 ( N ); // remove the center
    for ( int i=0; i<N; i++ )
    {
        q1[i] = pts1[i] - p1;
        q2[i] = pts2[i] - p2;
    }

    // compute q1*q2^T
    Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
    for ( int i=0; i<N; i++ )
    {
        W += Eigen::Vector3d ( q1[i].x, q1[i].y, q1[i].z ) * Eigen::Vector3d ( q2[i].x, q2[i].y, q2[i].z ).transpose();
    }
    cout<<"W="<<W<<endl;

    // SVD on W
    Eigen::JacobiSVD<Eigen::Matrix3d> svd ( W, Eigen::ComputeFullU|Eigen::ComputeFullV );
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();
    cout<<"U="<<U<<endl;
    cout<<"V="<<V<<endl;

    Eigen::Matrix3d R_ = U* ( V.transpose() );
    Eigen::Vector3d t_ = Eigen::Vector3d ( p1.x, p1.y, p1.z ) - R_ * Eigen::Vector3d ( p2.x, p2.y, p2.z );

    // convert to cv::Mat
    R = ( Mat_<double> ( 3,3 ) <<
          R_ ( 0,0 ), R_ ( 0,1 ), R_ ( 0,2 ),
          R_ ( 1,0 ), R_ ( 1,1 ), R_ ( 1,2 ),
          R_ ( 2,0 ), R_ ( 2,1 ), R_ ( 2,2 )
        );
    t = ( Mat_<double> ( 3,1 ) << t_ ( 0,0 ), t_ ( 1,0 ), t_ ( 2,0 ) );
}

2.非线性优化BA

仍然是构造一个图优化问题，这里我们把相机位姿作为优化变量，3D点对之间的坐标变换作为误差项。由于g2o没有为我们提供3D到3D的边，因此需要我们自己来定义。这是一个一元边，观测量即3D点的维度为3，代码如下所示

// g2o edge
class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, g2o::VertexSE3Expmap>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    EdgeProjectXYZRGBDPoseOnly( const Eigen::Vector3d& point ) : _point(point) {}

    virtual void computeError()
    {
        const g2o::VertexSE3Expmap* pose = static_cast<const g2o::VertexSE3Expmap*> ( _vertices[0] );
        // measurement is p, point is p'
        _error = _measurement - pose->estimate().map( _point );
    }

    virtual void linearizeOplus()
    {
        g2o::VertexSE3Expmap* pose = static_cast<g2o::VertexSE3Expmap *>(_vertices[0]);
        g2o::SE3Quat T(pose->estimate());
        Eigen::Vector3d xyz_trans = T.map(_point);
        double x = xyz_trans[0];
        double y = xyz_trans[1];
        double z = xyz_trans[2];

        _jacobianOplusXi(0,0) = 0;
        _jacobianOplusXi(0,1) = -z;
        _jacobianOplusXi(0,2) = y;
        _jacobianOplusXi(0,3) = -1;
        _jacobianOplusXi(0,4) = 0;
        _jacobianOplusXi(0,5) = 0;

        _jacobianOplusXi(1,0) = z;
        _jacobianOplusXi(1,1) = 0;
        _jacobianOplusXi(1,2) = -x;
        _jacobianOplusXi(1,3) = 0;
        _jacobianOplusXi(1,4) = -1;
        _jacobianOplusXi(1,5) = 0;

        _jacobianOplusXi(2,0) = -y;
        _jacobianOplusXi(2,1) = x;
        _jacobianOplusXi(2,2) = 0;
        _jacobianOplusXi(2,3) = 0;
        _jacobianOplusXi(2,4) = 0;
        _jacobianOplusXi(2,5) = -1;
    }

    bool read ( istream& in ) {}
    bool write ( ostream& out ) const {}
protected:
    Eigen::Vector3d _point;
};

void bundleAdjustment (
    const vector< Point3f >& pts1,
    const vector< Point3f >& pts2,
    Mat& R, Mat& t )
{
    // 初始化g2o
    typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose维度为 6, landmark 维度为 3
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>(); // 线性方程求解器
    Block* solver_ptr = new Block( linearSolver );      // 矩阵块求解器
    g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm( solver );

    // vertex
    g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
    pose->setId(0);
    pose->setEstimate( g2o::SE3Quat(
        Eigen::Matrix3d::Identity(),
        Eigen::Vector3d( 0,0,0 )
    ) );
    optimizer.addVertex( pose );

    // edges
    int index = 1;
    vector<EdgeProjectXYZRGBDPoseOnly*> edges;
    for ( size_t i=0; i<pts1.size(); i++ )
    {
        EdgeProjectXYZRGBDPoseOnly* edge = new EdgeProjectXYZRGBDPoseOnly(
            Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z) );
        edge->setId( index );
        edge->setVertex( 0, dynamic_cast<g2o::VertexSE3Expmap*> (pose) );
        edge->setMeasurement( Eigen::Vector3d(
            pts1[i].x, pts1[i].y, pts1[i].z) );
        edge->setInformation( Eigen::Matrix3d::Identity()*1e4 );
        optimizer.addEdge(edge);
        index++;
        edges.push_back(edge);
    }

    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    optimizer.setVerbose( true );
    optimizer.initializeOptimization();
    optimizer.optimize(10);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2-t1);
    cout<<"optimization costs time: "<<time_used.count()<<" seconds."<<endl;

    cout<<endl<<"after optimization:"<<endl;
    cout<<"T="<<endl<<Eigen::Isometry3d( pose->estimate() ).matrix()<<endl;

}

ref 3D-3D相机位姿估计

参考：

1.https://blog.csdn.net/u011178262/article/details/89685134

2.https://blog.csdn.net/u011178262/article/details/85016981(雅各比)

3.https://www.jianshu.com/p/504f0e5d9c26

原文链接：https://blog.csdn.net/weixin_39752599/article/details/103497938

视觉SLAM总结-前端视觉里程计-特征点法

一、2D-2D相机位姿估计

二、3D-2D相机位姿估计

1.直线线性变换法DLT

2. 三对点匹配P3P算法

3.非线性优化BA

三、3D-3D相机位姿估计

1.SVD线性求解

2.非线性优化BA

标签云

近期文章

分类

视觉SLAM总结-前端视觉里程计-特征点法

一、2D-2D相机位姿估计

二、3D-2D相机位姿估计

1.直线线性变换法DLT

2. 三对点匹配P3P算法

3.非线性优化BA

三、3D-3D相机位姿估计

1.SVD线性求解

2.非线性优化BA

相关文章