1.缺项幂级数的解法
2.函数可导、可微、连续和偏导数连续之间的关系


答案:D
3.曲面的切平面存在–>>某点可微时
4.求函数是否有极限

答案:C
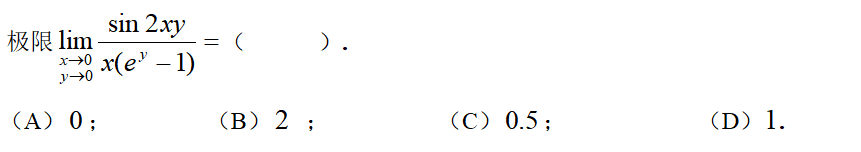
答案:B
思路:把sin2xy换成2xy,然后对y求偏导
这里涉及到一个问题:运用洛必达的时候是求全导还是偏导也可以
5.求多元函数的极限问题
- 判断极限是否存在可以让它趋于某一直线y=kx(ppt44)
- 利用之前学过的对表达式化简和转化
6.二重积分计算步骤
- 画图
- 选坐标系
- 选择积分次序
- 计算
7.求多元函数的极值
极值点只可能在驻点或使偏导数 不存在的点中产生
- 没有约束条件的时候(课本P113)


- 有约束条件的时候(P118)

- 有约束条件时的一个例子

我的看法:先假设在第一象限内的能取得最大值的点,对于相应的面积函数,xyz有在椭球上,就转化成有约束条件的求极值问题,就可以用拉格朗日乘数法来解
8.三重积分
几何意义:空间不规则物体的质量

解法:

答案:B
解法:

解法:
9.二重积分
1.几何意义
曲顶柱体体积
平面薄片质量
2.计算二重积分的时候,看到表达式比较复杂,就要考虑奇偶性来化简

3.二重积分的导数
- 关键是根据积分的对象之间是否向影响来构造函数

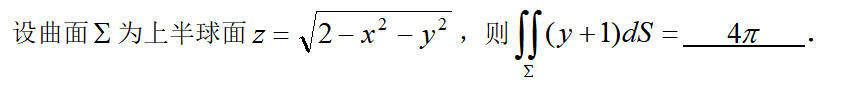
4.其他

答案:D
解法:高斯公式
例题:

10.曲线和曲面积分还要再看看
11.方向导数

12.傅里叶级数


答案:(1+pi)/2
13.函数展开成幂级数

14.幂级数与和函数的相杀
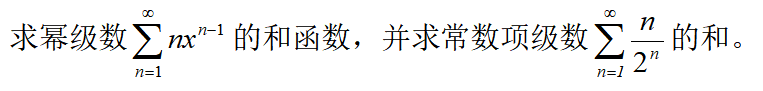




15.拉格朗日乘数法


16.方向导数是一个数值,梯度是一个向量
17.敛散性
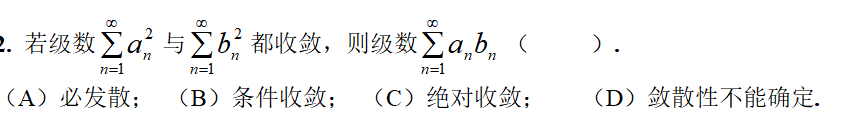
答案:C
18.积分与路径无关和存在全微分(P208)
版权声明:本文为weixin_50970194原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。