---

严平稳和宽平稳

严平稳

严平稳是真的很严格 ，可以用分布函数族来定义，也可以用密度函数族来定义 ( 由于特征函数和它们的一一对应性，所以也可以用特征函数族来证明 )

• 分布不会随着时间而改变
  ||
  ||
  V
• 期望是个常量（因为分布函数与 t 无关，积分的时候就会把 t 消掉 ）

所以随机过程的期望一般来说不是常量（还是个随机过程） ，就像随机过程的导数和积分也一般来说不是常量，还是个随机过程

• 证严平稳的思路

图

宽平稳

宽平稳则是从数字特征函数方面进行下手定义的

分布改变只和时间差有关联

• 可以用两种方式刻画（ 自相关 和 协方差 ） 因为只要期望是常数 ，自相关和协方差之间只相差一个变量而已（分析详见琐碎联想）

严平稳和宽平稳的关系

• 没有特殊说明的话 ，我们指的平稳过程都是宽平稳，因为这样的过程比较好表达，只用数字特征表达就可以了

• 两者其实没有什么必然的联系。严平稳是很严格的，宽平稳实际上只要满足相应的数字特征即可（均值和方差相同但是分布不一致的随机过程太多 了）满足是二阶矩的严一定是宽，满足宽的正态分布一定是严

• 求出分布密度函数里面，和t₁以及t₂无关，只与

  τ

  \tau

  τ = t₂ – t₁有关

  • 因为分布密度函数只与$\tau$有关，那么分布函数是分布密度函数的积分，也只与$\tau$有关，所以可以看出这是个严平稳过程
    
    老肖这也不知道在证啥…密度函数族只与时间之差有关的话，积出来的分布函数族还是只与时间之差有关= =

宽其实和严关系不大 只是满足了那几个数字特征的一个过程而已

宽平稳的性质

• 简单证明
  • 第一行 共轭对称性
  • 第二行就是利用R(0)就是EX²的以及DX非负的性质
  • 第三行利用第二行的性质以及斯沃茨不等式的性质（证明协方差的时候 还用到了Cov($\tau$) =R($\tau$) –${\mu }^2$ 【这是对于自相关和自协方差来说，如果是互相关和互协方差就不能这么写了】

平稳过程的自相关函数非负如何理解？ -》 不必纠结，任何过程和的自相关函数都是非负的

这是关于求导的性质

注意，性质1，等式右边有个负号，是因为

R

(

τ

)

=

R(\tau)=

R(τ)=R(s-t)，先对s求导(这一步没毛病），再对 t 求导，但是此时 t 前面有个负号啊别忘了

还没摸清这个性质有啥用…

例题

联合平稳过程

定义

互相关函数与 t 无关，仅与

τ

\tau

τ相关

平稳过程的互相关函数也是与t无关的话，他们的线性组合也平稳…

• 性质证明
  • 第一个的话，跟自相关函数是一样的，共轭对称性
  • 第二个的话，用斯沃茨不等式
  • 第三个的话，就是用定义证出来的，如下
    

各态历经性( 均方遍历性 )

意义

可以用时间 ( t ) 上的平均来代替样本函数上的采样( w )平均

• 定义
  
  
  非退化随机变量的意思是，<ξ(t)>算出来不会是是个常数，而Eξ(t)是常数，所以肯定不相等

• 这里证明的思路就是：

1. 先对ξ(t)求时间平均 ( 对t求平均积分然后再求均方极限 )，看看和自己本身的期望是不是相同的( 这个时候是对非 t 参数进行积分 ) 。如果ok下一步
2. 再对ξ(t)ξ( t+$\tau$)求时间平均 ( 对t求平均积分然后再求均方极限 )，看看和自己本身的自相关函数是不是相同的( 自相关函数就是ξ(t)ξ( t+$\tau$)对参非t参数进行积分 )

• 大概可以看出含义是：
  如果均方遍历的，我们就可以用某一个时刻的情况去估计整体时刻的情况

至于为什么只考察一阶矩和二阶矩 ，因为高阶矩（>2) 被 低阶矩( 《=2 ) 控制，而一阶矩被二阶矩控制 （Eξ <= Eξ² )

均值遍历定理

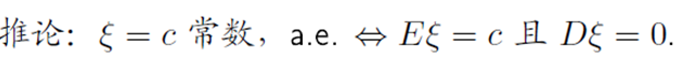
均值遍历性 等价于 均值为常数，方差为0

自相关函数遍历定理

例题

---

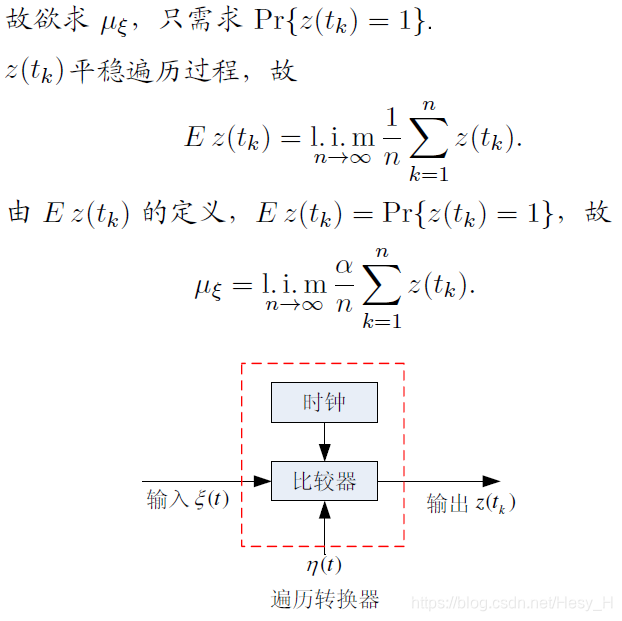
琐碎联想

• 随机过程中的协方差函数，如果取t1=t2 实际上跟方差函数很像
• 方差是EX² – E²X
• 协方差是R(t₁,t₂) – Et₁Et₂