概率论中独立事件的讨论

开始之前，我们要明确描述一个问题的概率问题时，必须准确把握这个”样本空间”，概率书上一般称这个为所有可能的结果构成的集合为”样本空间”。如果甲在描述的一个问题的样本空间为A,它基于这个A的出一个概率 $P_{1}$ ，而乙在另外一个不同的样本空间B中得出一个概率 $P_{2}$ ，那么讨论 $P_{1}$ 和 $P_{2}$ 的关系需要谨慎，要不然就是驴唇不对马嘴。

1. 条件概率

学习条件概率的时候会碰到下面的条件概率公式：

$P(E|F)=\frac{P(EF)}{P(F)}, P(F)>0$

这个式子的意思就是F事件发生的条件下，E事件发生的概率。从字面上，主观的感受觉这个是很容易被理解的一个公式。要深刻理解这个条件概率公式的话，是需要深刻理解这里面讨论概率问题时”样本空间”的切换。用“维恩图”来理解更容易掌握实质：

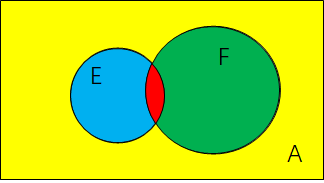
$P(E|F)=\frac{S_{red}}{S_{F}}$ ，即条件概率P(E|F)等于红色部分面积（EF相交部分面积）除以F事件面积（绿色+红色面积）

也就是说求 $P(E|F)$ 时候的样本空间是以F事件的样本空间为参考的，这与 $P(E)=\frac{S_{E}}{S_{A}}$ （即E事件面积除以A原始样本空间面积）。

也就是说 $P(E|F)$ 和 $P(E)$ 两个概率所参考的样本空间完全不一样：

$P(E)$ 是基于原始样本空间A， $P(E|F)$ 是基于新的样本空间F。

2. 事件独立

定义：对于事件E和事件F,如果满足下面的公式，那么称它们是独立的。若两个事件E和F不独立，则称它们是相依的，或者相互不独立。

$P(EF)=P(E)P(F)$

因此如果事件E和事件F独立，那么肯定满足下满的式子：

$P(E)=P(E|F)$

观察上面的维恩图，可知:

$\frac{S_{red}}{S_{F}}=\frac{S_{E}}{S_{A}}$

这也就说明了事件F的样本空间对事件E样本空间的切割后这部分(即形成维恩图中红色部分空间)在F中的比例和事件E在原来总体样本空间A中的比例是一致的，实际上这种”同比例切割”的特性，是确定F与E是否独立的一个标志，如果F事件样本空间同比例切割E事件空间，那么E和F就是独立的。这样子的描述和”F事件的发生并不影响E发生的概率，那么E和F就是独立的”, 事实上这样子的描述在主观上有时候不是特别容易判断的。用”同比例切割”有时候更容易判断两个事件是否是独立的。相反的，不能同比例切割的话，那可以判断E和F是不独立的。

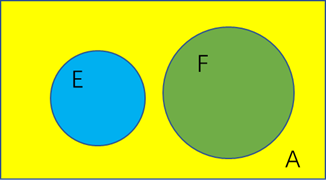
利用这个结论，观察上面这个维恩图，它告诉我们，E和F事件没有相交的部分，按照”同比例切割”的观点，F事件和E事件是”不独立”的！当然也可以利用是否满足公式 $P(EF)=P(E)P(F)$ 方式去验证独立性。这个图告诉我们：

两个不相交的事件，反而是”相互不独立”的。除了一种情况，事件E不可能出现，也就是P(E)=0。

这给我们一种新的认识：世界上两个没有任何交集的人，却相互不独立。除非你不存在。

造成这种错觉的原因是，讨论问题的角度不一样，相交讨论的是两个事件的集合，而”独立性”与否讨论的是比例(也就是概率)的问题。另外，概率论中的”独立”都是特别针对概率值的影响的，而人的独立性讨论的是人格特征。概率论中只是借用了”独立”这个词，概念上被赋予了严格的数学意义。

例1. 从一副洗好的52张扑克牌里随机抽取一张牌，令E表示事件”抽取的牌为一张A”，令F表示事件”抽取的牌为一张黑桃”，那么E和F就是独立的。因为P(EF)=1/52，而P(E)=4/52且P(F)=13/52。

这个例子也可以用”同比例分割”的方法来判断。原始样本空间大小为52，事件E空间大小有4（因为有4张牌A），因此事件E在原来空间中的分割比例时4/52。相交事件EF样本空间（既是牌A又是黑桃）1，事件F的样本空间很明显是13（因为有13张黑桃），因此，EF在F中的分割比例为1/13。4/52=1/13，因此是独立的。

例2. 掷两枚均匀的骰子，令 $E_{1}$ 表示事件”骰子点数和为6″，令F表示事件”第一枚骰子点数为4″，那么