坐标旋转

坐标旋转包含绕x、y、z轴旋转，在右手坐标系中，x-翻滚(roll)，y-俯仰(pitch)，z-航向(yaw)，详细可参考维基百科。自动驾驶中，还需要将车体坐标系转换到大地坐标系，此时还需要当前车体的位置、姿态。

从baseLink到map的转换关系为:先绕x轴旋转,在绕y轴旋转,最后绕z轴旋转,即左乘为Rzyx, 然后在平移t. 从map到baseLink的转换关系正好相反,先平移-t, 然后绕z轴旋转,在绕y轴,最后绕x轴. 注意,此时旋转的角度与baseLink到map的正好相反.

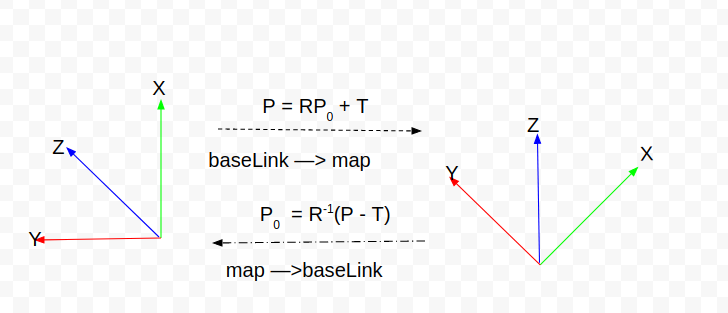
已知当前车体坐标系的点云cloud，当前车体的位置即姿态x, y, z, roll, pitch, yaw。通过pcl::getTransformation获取从车体坐标系到大地坐标系的旋转矩阵。

Eigen::Affine3f transCur = pcl::getTransformation(x, y, z, roll, pitch, yaw);

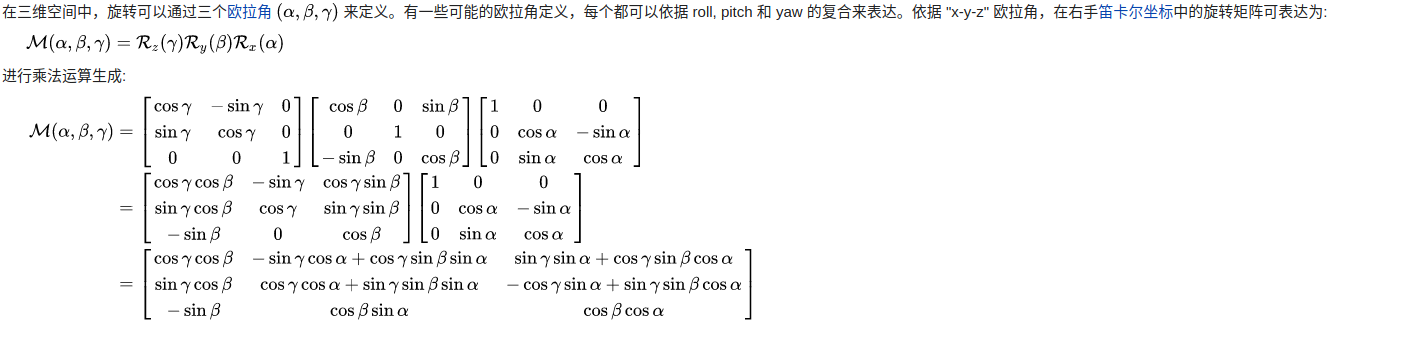
其中getTransformation的计算过程如下，先计算旋转，在加上平移量x, y, z：计算过程如下

Eigen::Matrix3f getRomateZYXMat(float yaw, float pitch, float roll){
    float cz = cos(yaw);
    float sz = sin(yaw);
    float cx = cos(roll);
    float sx = sin(roll);
    float cy = cos(pitch);
    float sy = sin(pitch);

    Eigen::Matrix3f Rx, Ry, Rz, mat;

    Rx << 1,   0, 0,
          0,  cx, -sx,
          0,  sx, cx;

    Ry << cy, 0, sy,
           0, 1, 0,
         -sy, 0, cy;

    Rz << cz, -sz, 0,
          sz,  cz, 0,
          0 ,   0, 1;

    mat = Rx * Ry * Rz;

    return mat;
}

pcl中中的计算方式,二者的结果是一样的.

template <typename Scalar> void 
pcl::getTransformation (Scalar x, Scalar y, Scalar z, 
                        Scalar roll, Scalar pitch, Scalar yaw, 
                        Eigen::Transform<Scalar, 3, Eigen::Affine> &t)
{
  Scalar A = cos (yaw),  B = sin (yaw),  C  = cos (pitch), D  = sin (pitch),
         E = cos (roll), F = sin (roll), DE = D*E,         DF = D*F;

  t (0, 0) = A*C;  t (0, 1) = A*DF - B*E;  t (0, 2) = B*F + A*DE;  t (0, 3) = x;
  t (1, 0) = B*C;  t (1, 1) = A*E + B*DF;  t (1, 2) = B*DE - A*F;  t (1, 3) = y;
  t (2, 0) = -D;   t (2, 1) = C*F;         t (2, 2) = C*E;         t (2, 3) = z;
  t (3, 0) = 0;    t (3, 1) = 0;           t (3, 2) = 0;           t (3, 3) = 1;
}

最后pcl::transformPointCloud将cloud转换到大地坐标系。

pcl::transformPointCloud(cloud, *colorPclPtr, transCur);

void se3 (const float* src, float* tgt) const
{
     const Scalar p[3] = { src[0], src[1], src[2] };//车体坐标系的点  
     tgt[0] = static_cast<float> (tf (0, 0) * p[0] + tf (0, 1) * p[1] + tf (0, 2) * p[2] + tf (0, 3));
     tgt[1] = static_cast<float> (tf (1, 0) * p[0] + tf (1, 1) * p[1] + tf (1, 2) * p[2] + tf (1, 3));
     tgt[2] = static_cast<float> (tf (2, 0) * p[0] + tf (2, 1) * p[1] + tf (2, 2) * p[2] + tf (2, 3));
     tgt[3] = 1;
}

如果大地坐标系下的点云想转换到车体坐标系，则需要先减去当前车体的坐标，然后在反方向旋转得到原始点云。

Eigen::Matrix3f getRomateXYZMat(float roll, float pitch, float yaw){
    float cz = cos(yaw);
    float sz = sin(yaw);
    float cx = cos(roll);
    float sx = sin(roll);
    float cy = cos(pitch);
    float sy = sin(pitch);

    Eigen::Matrix3f Rx, Ry, Rz, mat;

    Rx << 1,   0, 0,
          0,  cx, -sx,
          0,  sx, cx;

    Ry << cy, 0, sy,
           0, 1, 0,
         -sy, 0, cy;

    Rz << cz, -sz, 0,
          sz,  cz, 0,
          0 ,   0, 1;

    mat = Rz * Ry * Rx;

    return mat;
}

也可以按照前面的公式，求出旋转和平移的联合矩阵$\left [R^{-1} : R^{-1} * -T \right ] $。

 //获取反向旋转矩阵
Eigen::Matrix3f transCurMap = getRomateZYXMat(-yaw, -pitch, -roll);
//平移向量
Eigen::MatrixXf t0(3,1);
t0<<-x, -y, -z;
Eigen::MatrixXf transMat(3, 1);
transMat = transCurMap.matrix() * t0;

最后，如果通过TF获取base_link和map的坐标转换关系ts(base_link to map)、tsMap(map to base_link)，发现与上述自己计算的一致。

                //Rzyx轴旋转
                auto tsStamped = buffer.lookupTransform("map", "base_link", ros::Time(0));
                //Rzyx轴旋转
                auto tsStampedMap = buffer.lookupTransform("base_link", "map", ros::Time(0));
                Eigen::Matrix4f ts = tf2::transformToEigen(tsStamped.transform).matrix().cast<float>();
                Eigen::Matrix4f tsMap = tf2::transformToEigen(tsStampedMap.transform).matrix().cast<float>();