编译原理: Thompson 构造法(正则表达式 转 NFA)
文章目录
简介
编译过程往往依赖于有限状态机的构建,其中最具代表性的就是正则表达式(Regular Expression),当然有限状态机的应用不止于此,在词法、语法分析都占有很重要的地位。
接下来几篇将会依序介绍由正则表达式(RegExp)构建确定有限状态机(DFA)的流程:
- Thompson 构造法:正则表达式 RegExp -> 不确定有限状态机 NFA
- 子集构造法:不确定有限状态机 NFA -> 确定有限状态机 DFA
- 最小化:最小化确定有限状态机 DFA
- 验证:DFA 转换为的等价正则表达式并验证等价
本篇将会介绍解析正则表达式的第一步骤:Thompson 构造法
参考
| 什么是NFA(不确定的有穷自动机)和DFA(确定的有穷自动机) | https://www.cnblogs.com/AndyEvans/p/10240790.html |
| Thompson构造法 | https://www.beichengjiu.com/mathematics/173003.html |
| 从正则表达式到NFA:Thompson构造法 | https://www.cnblogs.com/peng-lei/articles/5755107.html |
正文
什么是状态机
在开始介绍 Thompson 构造法之前我们先来了解一下 NFA、DFA 究竟是啥,又为啥我们要透过简介提到的流程来识别正则表达式
- 非确定有限状态机 NFA = NonDeterministic Finite Automation
- 确定有限状态机 DFA = Deterministic Finite Automation
两者的构成元素就是一个有限状态机 FA = Finite Automation
有限状态机 FA
我们可以以下列五个元素的集合表示一个有限状态机:
A
=
(
S
,
∑
,
δ
,
s
0
,
F
s
)
A = (S, \sum, \delta, s0, Fs)
A=(S,∑,δ,s0,Fs)
-
S
S
S:状态集合 -
∑
\sum
∑:输入的字母表(输入字符的集合) -
δ
\delta
δ:状态转移函数,δ
:
S
×
∑
→
S
\delta: S \times \sum \to S
δ:S×∑→S -
s
0
s0
s0:初始状态,s
0
∈
S
s0 \in S
s0∈S -
F
F
F:终止状态,F
⊆
S
F \subseteq S
F⊆S
一个有限状态机从初始状态
s
0
s0
s0 出发,到终止状态
F
F
F 结束,中间透过输入字符
c
∈
∑
c \in \sum
c∈∑ 和转移函数
δ
\delta
δ 决定状态的变化。
NFA vs DFA
两种的差别在于确定和不确定,也就是对于转换函数
δ
\delta
δ 的限制:
- DFA 的转换函数
δ
\delta
δ 对于一组输入(
s
,
c
)
,
s
∈
S
,
c
∈
∑
(s,c), s \in S, c \in \sum
(s,c),s∈S,c∈∑ 有唯一确定的输出,即∣
δ
(
s
,
c
)
∣
=
1
|\delta(s, c)| = 1
∣δ(s,c)∣=1 - 而 NFA 的转换函数对于同一种输入则可能存在多个
输出状态,即∣
δ
(
s
,
c
)
∣
>
0
|\delta(s, c)| > 0
∣δ(s,c)∣>0
现在我们知道要能够正确并顺序解析正则表达式并加以利用我们需要构建出一个 DFA,因为 NFA 在解析时存在状态转换的不确定性
Thompson 构造法
接下来就进入本篇的重点:Thompson 构造法(正则表达式 -> NFA)
Thompson 构造法将定义基本单元以及三种合并基本单元的原则,接下来我们使用两个正则表达式作为例子逐步构造
-
a
(
b
∣
c
)
∗
a(b|c)*
a(b∣c)∗ -
(
a
∣
b
)
∗
a
b
b
(a|b)*abb
(a∣b)∗abb
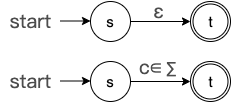
基本单元:单个字符
Thompson 构造法的第一步就是先构建所有基本单元,这边我们就为符号表中的每一个 符号
c
∈
∑
c \in \sum
c∈∑ 构建一个基本单元
接下来给出两个例子的基本单元集合
-
a
(
b
∣
c
)
∗
a(b|c)*
a(b∣c)∗

-
(
a
∣
b
)
∗
a
b
b
(a|b)*abb
(a∣b)∗abb
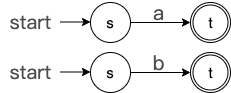
后面我们可以用下面的简图简化基本单元的表示

三种转换规则:并(或) |、连接
⋂
\bigcap
⋂、闭包 *
- 并:
a
∣
b
a|b
a∣b
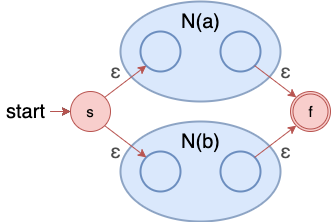
规则:另外添加一个起始状态和终止状态,起始状态可以转移到两个基本单元的起始状态,两个基本单元的终止状态可以转移到最终终止状态
- 连接:
a
b
ab
ab
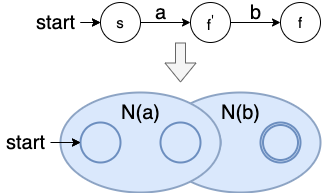
规则:连接操作就直接将前一个字符的终止状态于后一个字符的起始状态重叠就好了
- 闭包:
a
∗
a*
a∗
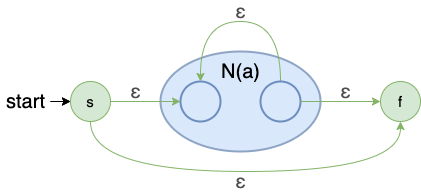
规则:对于一个闭包,
a
a
a 相当于是一个存在起始和终止状态的单元(可以替换成其他任意组成的复杂单元)可以重复 0 到多次,所以加入一个新的起始状态和终止状态,并使得
a
a
a 的终止状态能重新回到起始状态
示例
接下来给出两个例子使用 Thompson 转换后的 NFA
a
(
b
∣
c
)
∗
a(b|c)^{*}
a(b∣c)∗

(
a
∣
b
)
∗
a
b
b
(a|b)^{*}abb
(a∣b)∗abb
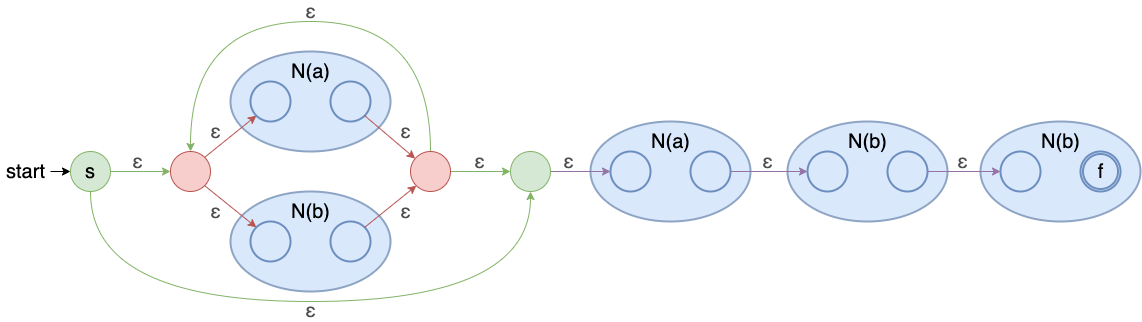
结语
到此我们就完成正则表达式到 NFA 的转换了,下一篇将延续本篇的结果,将 NFA 装换成 DFA。