文章目录
Reference
[1] Hung-yi Lee: https://youtu.be/OAKAZhFmYoI
1. Policy Gradient
一种policy-based方法,由策略网络直接输出动作。
1.1 Actor, Enviroment, Reward
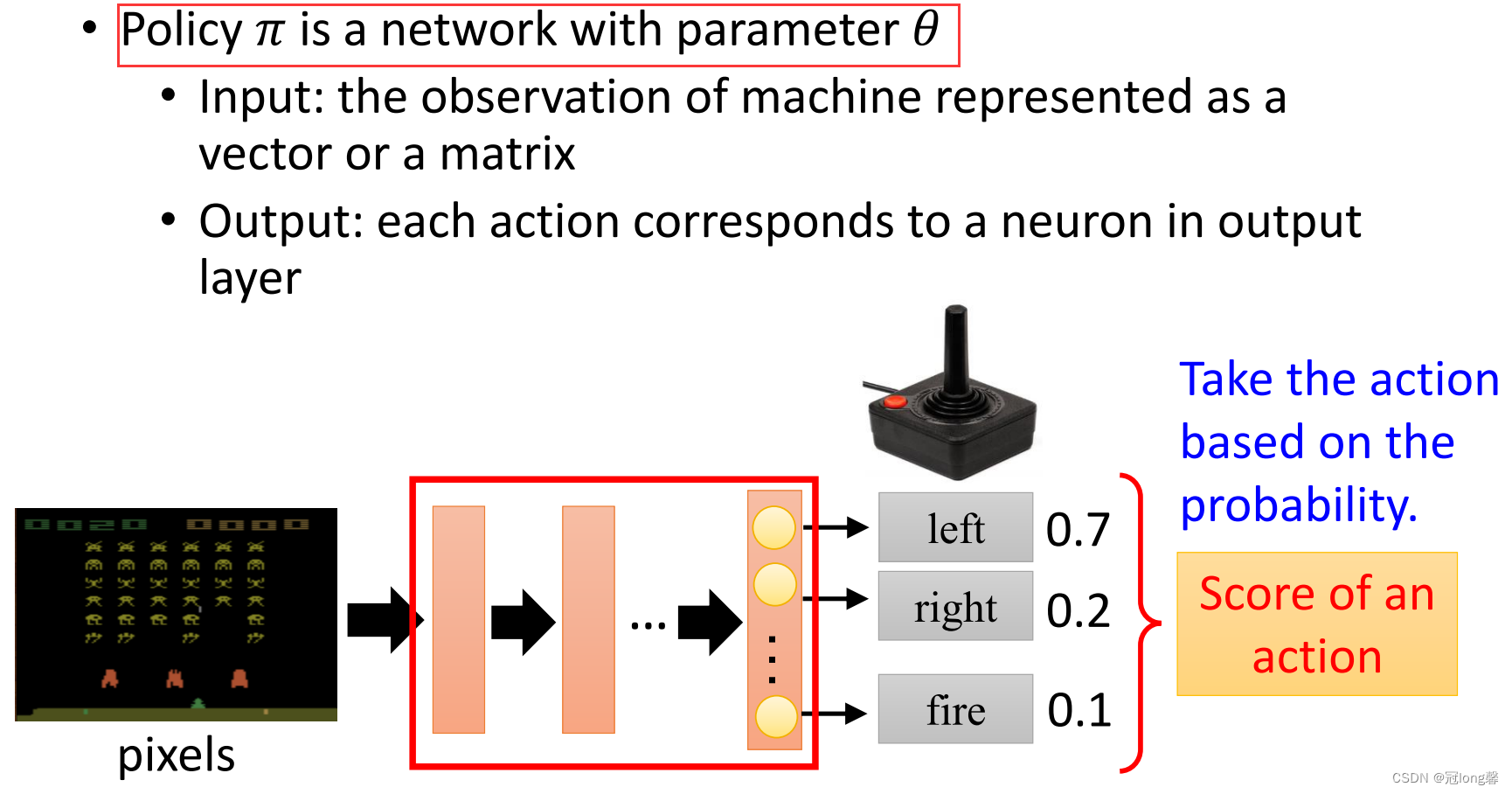
(1)Actor
Actor指策略网络
π
θ
\pi_\theta
πθ,输入状态s输出动作。
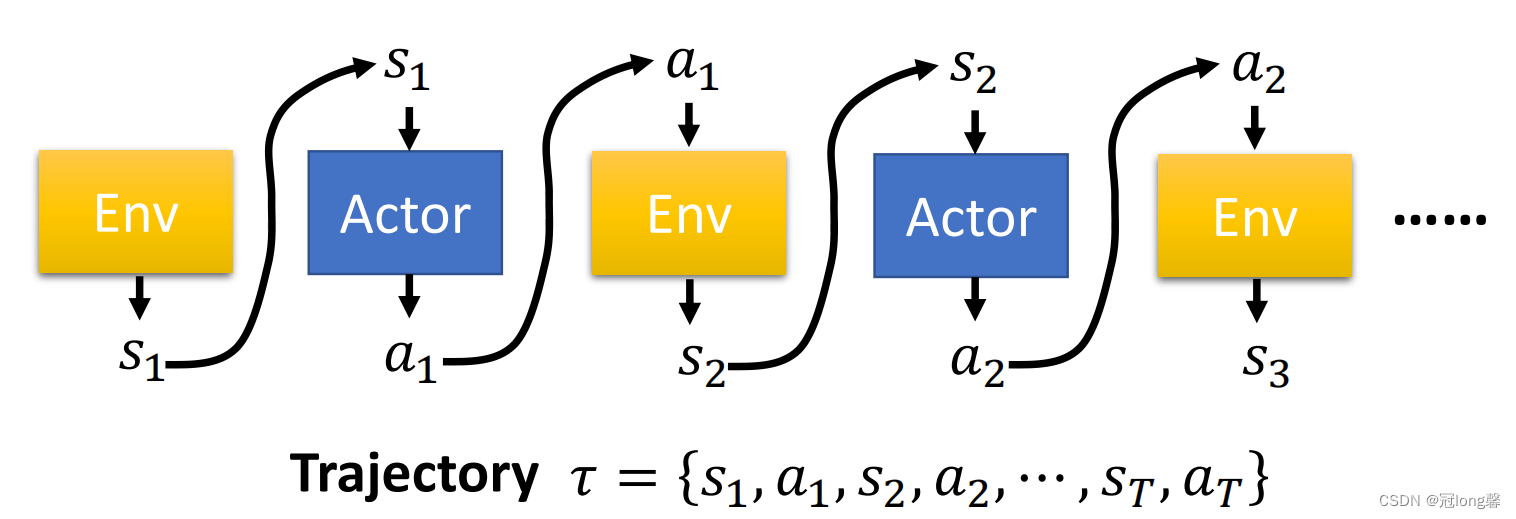
(2)Interaction Process
演员与环境的交互过程:将环境状态
s
i
s_i
si输入到actor,策略网络输出动作
a
i
a_i
ai。将动作
a
i
a_i
ai输入到环境中可以获得奖励和下一状态
R
i
+
1
,
s
i
+
1
R_{i+1},s_{i+1}
Ri+1,si+1。一条完整的轨迹
τ
\tau
τ由有限个状态动作对组成。
-
轨迹概率
p
θ
(
τ
)
p_\theta(\tau)
pθ(τ):由每个时间步上所处状态的概率与策略网络动作选择概率的乘积组成。
(注意:对θ
\theta
θ求导时与环境的状态概率无关,仅对策略选择概率求导)
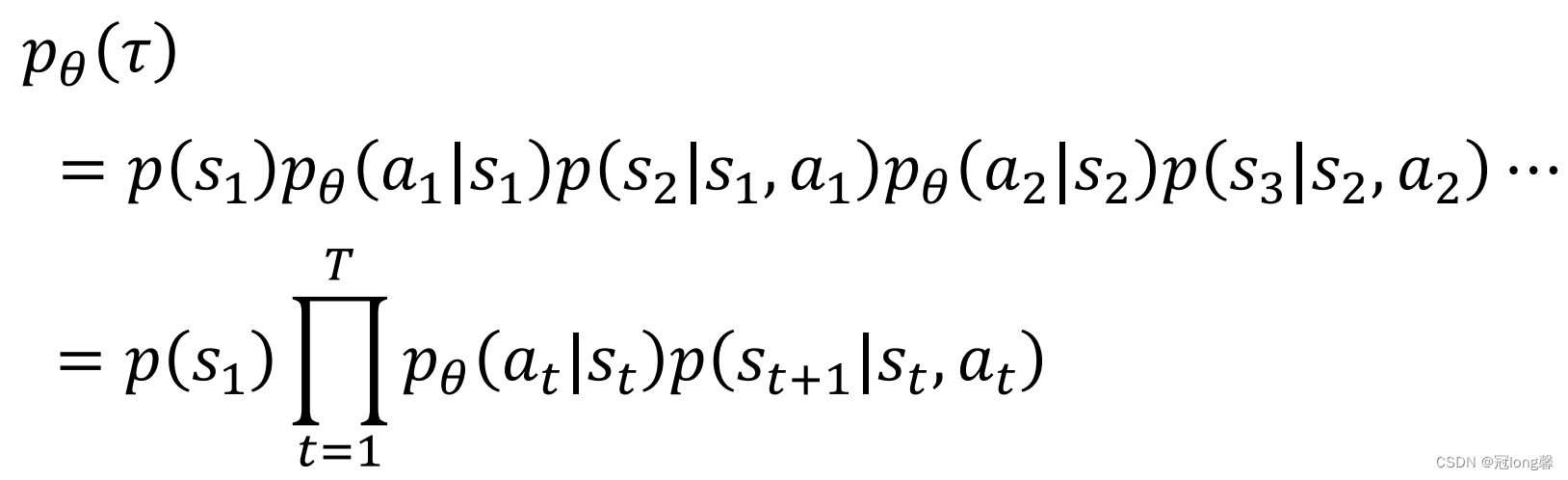
-
轨迹奖励总和:由一条抽样完整轨迹上所获得奖励求和获得。
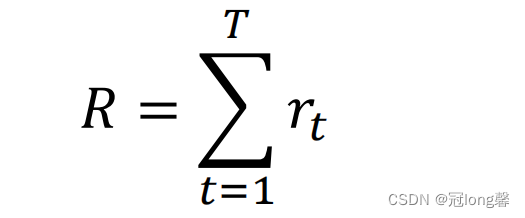
-
轨迹期望奖励:任意一条完整轨迹获得的奖励总和的平均值。
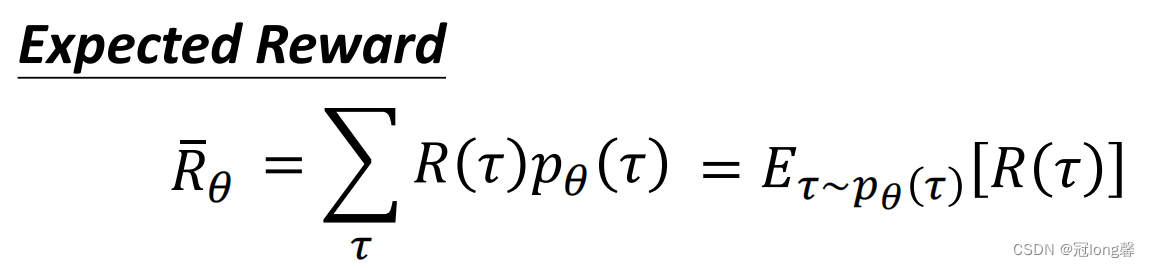
1.2 Gradient Descent
(1)Objective Function
希望学习得到的策略能最大化轨迹的期望奖励
R
θ
ˉ
\bar{R_\theta}
Rθˉ。
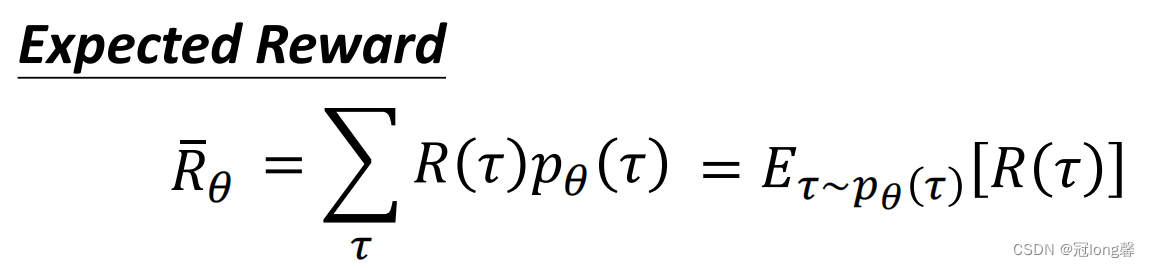
理解:直观上理解就是最优策略下,每条轨迹获得的奖励总和都能最大。
(2)Gradient
对目标函数函数求导,便可以获得
θ
\theta
θ的梯度

理解:
R
(
τ
n
)
R(\tau^n)
R(τn)认为是修正的权重,
∇
log
p
θ
(
a
t
n
∣
s
t
n
)
\nabla \log p_\theta(a_t^n|s_t^n)
∇logpθ(atn∣stn)认为是对每个状态动作对修正的方向。
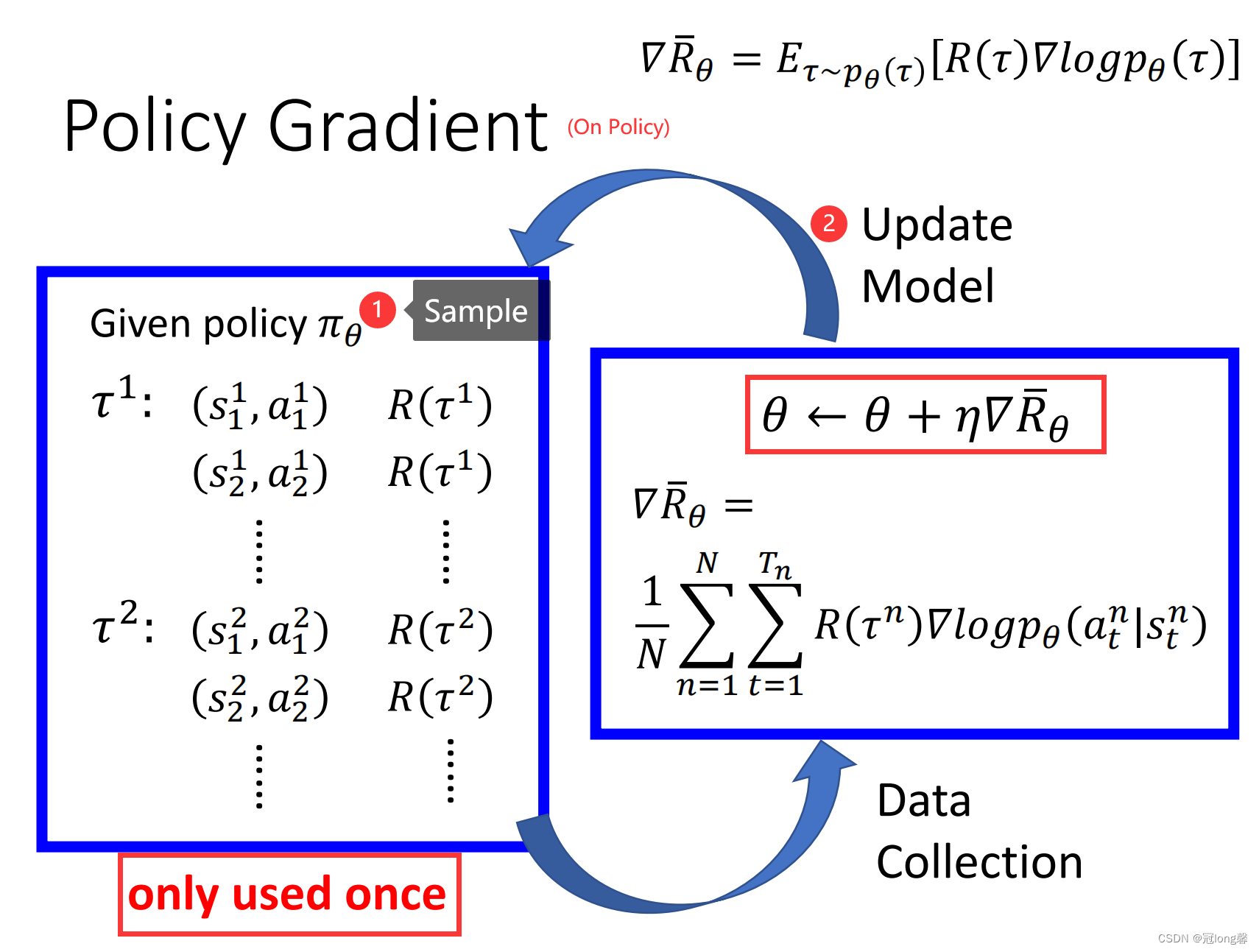
(3)Algorithm
每一轮先利用策略
π
θ
\pi_\theta
πθ获得大量轨迹,接着利用收集的轨迹计算梯度更新参数
θ
\theta
θ。因为每轮更新后参数
θ
\theta
θ的改变都会导致采样分布的变化,因此每轮收集的轨迹数据只能使用一次。
PPO算法在传统的策略梯度算法上做出了多处改进,下面我将逐个介绍它们。
1.3 Tip1: Add a Baseline
在策略梯度
∇
R
θ
ˉ
\nabla \bar{R_\theta}
∇Rθˉ计算时,对于同一轨迹上的所有状态动作对
(
s
t
,
a
t
)
(s_t,a_t)
(st,at)使用了相同的权重
R
(
τ
n
)
R(\tau^n)
R(τn)轨迹奖励总和进行了修正。
- 在理想状态下a, b, c三个状态动作对都能被采样到,当
R
(
τ
n
)
R(\tau^n)
R(τn)总是为正时下一次策略网络输出a, b, c的概率会增加。 - 但是因为不能保证状态动作对都被采样,没有被采样的状态动作对下一次策略网络输出的概率会下降,即使它的梯度为正。
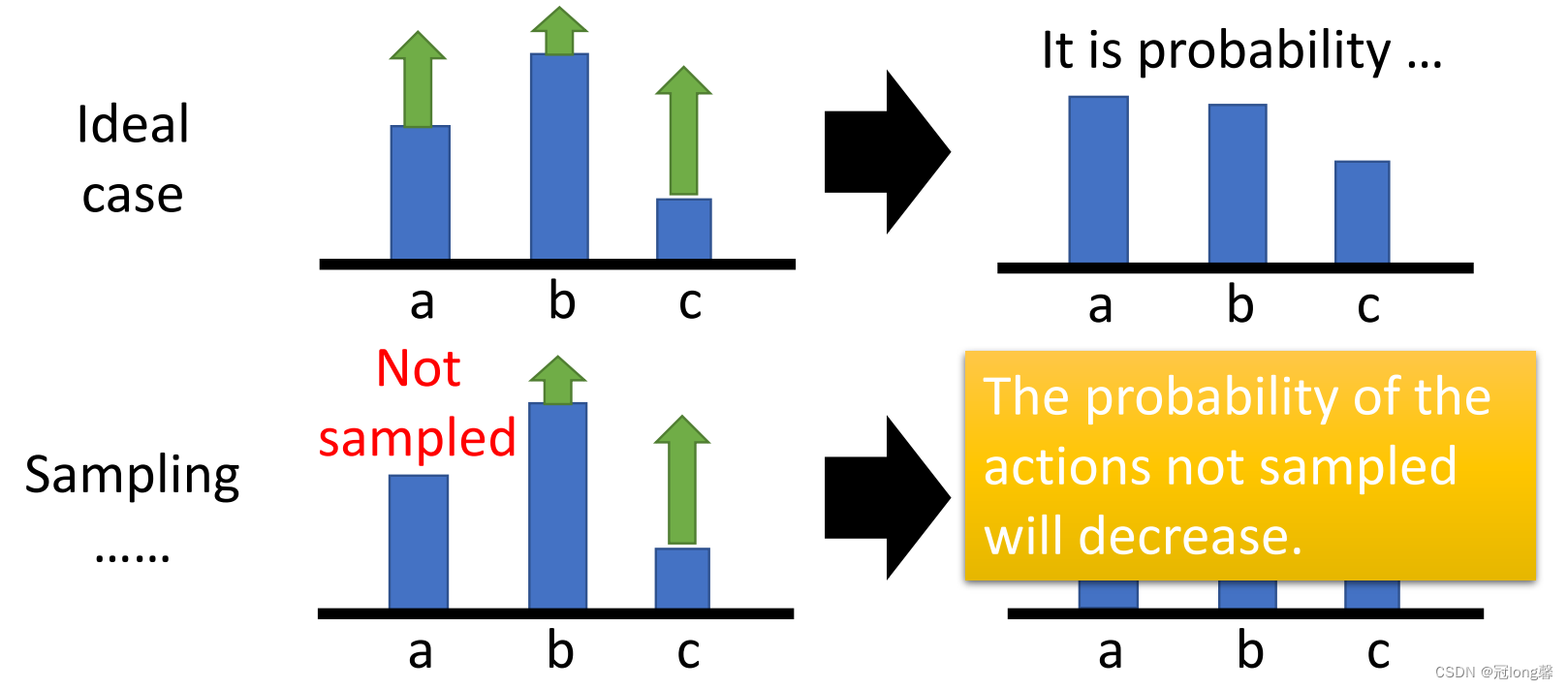
因此我们在权重部分减去baseline,即当前策略的平均奖励。这样改变权重将不总是为正的,未被采样的状态动作对的概率也不会自然下降了。
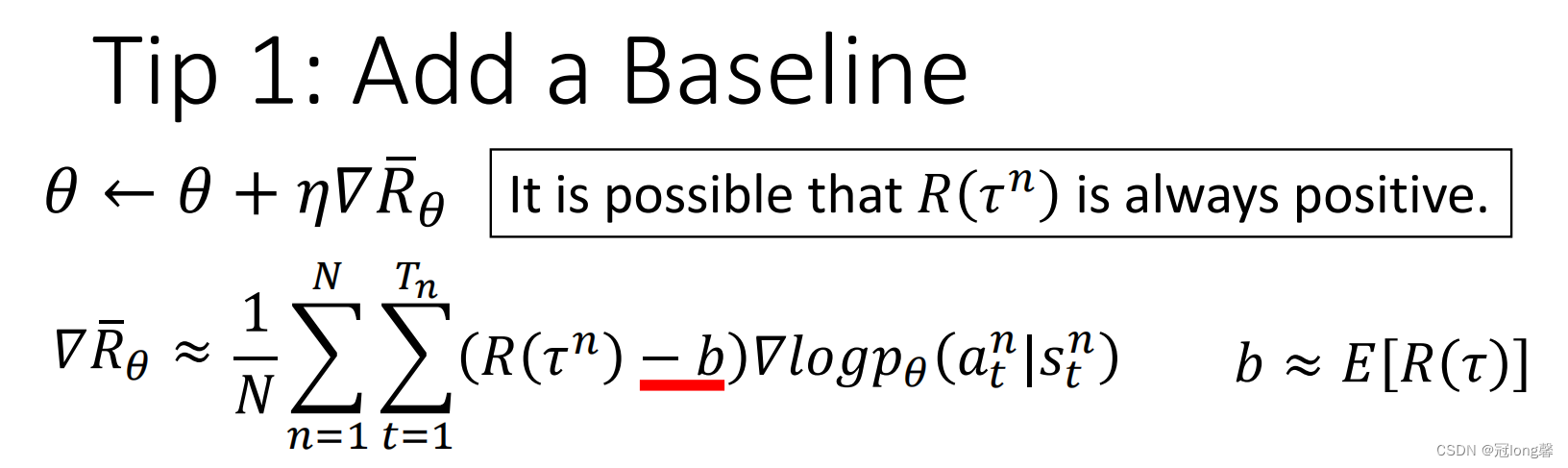
1.4 Tip2: Assign Suitable Credit
在策略梯度
∇
R
θ
ˉ
\nabla \bar{R_\theta}
∇Rθˉ中,同一轨迹上的所有状态动作对的修正权值相同,为
R
(
τ
n
−
b
)
R(\tau^n-b)
R(τn−b)。但是用一条轨迹的奖励总和衡量其中的所有状态动作对的好坏并不合理。
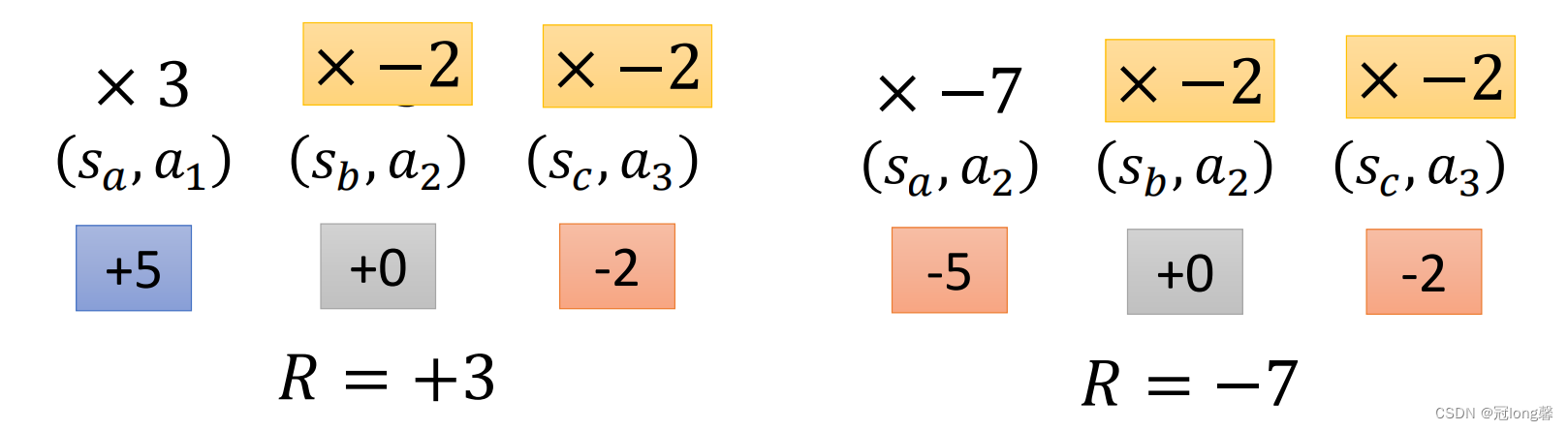
如上图所示,在第一条轨迹中
(
s
c
,
a
3
)
(s_c,a_3)
(sc,a3)的奖励为-2,此时应该降低
(
s
c
,
a
3
)
(s_c,a_3)
(sc,a3)的概率。但是因为轨迹的奖励总和为+3,所以会鼓励
(
s
c
,
a
3
)
(s_c,a_3)
(sc,a3),
(
s
c
,
a
3
)
(s_c,a_3)
(sc,a3)的概率反而增加了。所以我们需要修改更新权值,使之贴合于每个状态动作对。
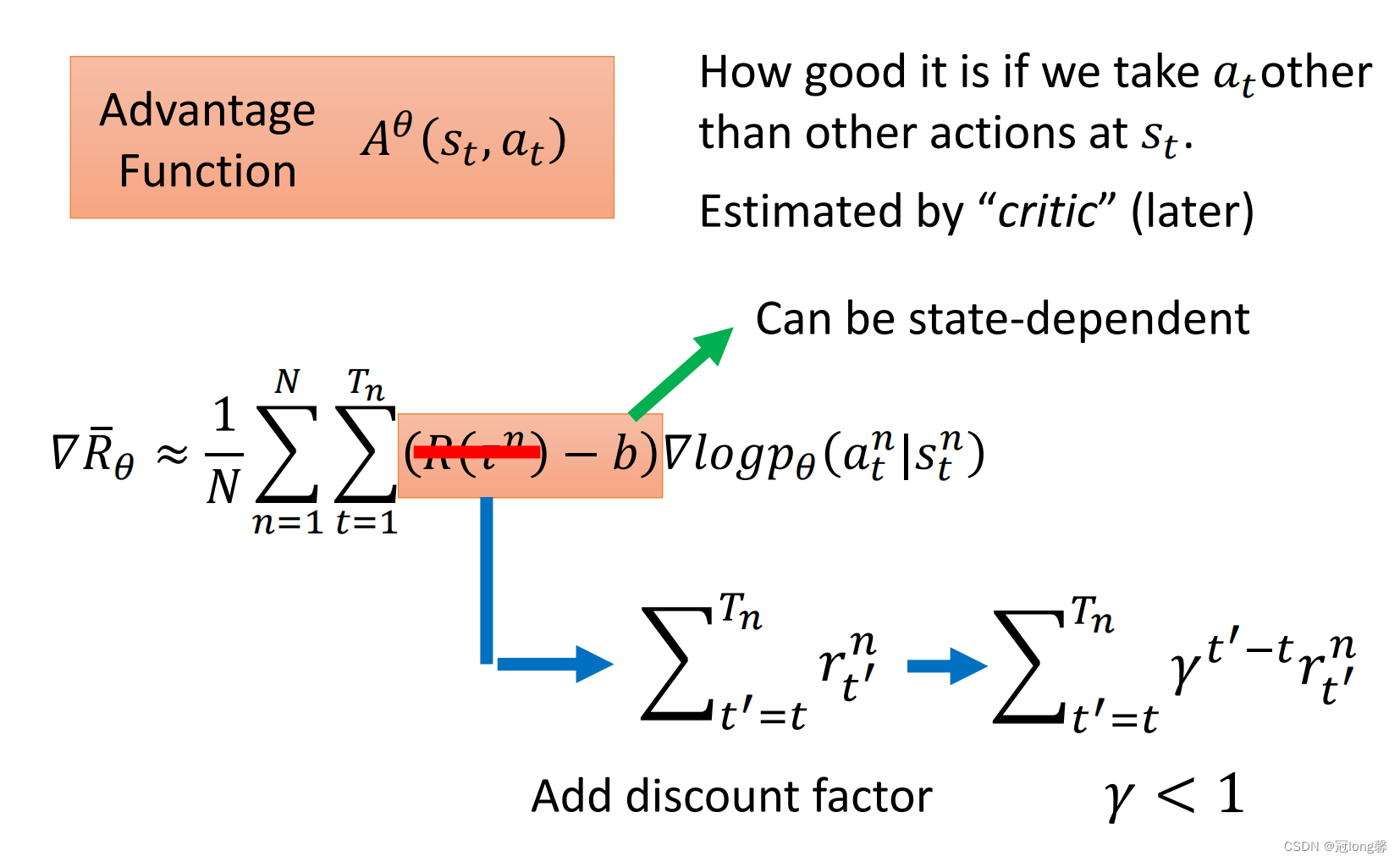
于是我们使用了折扣奖励替代了轨迹的奖励总和,我们将每个状态动作对的奖励折扣与baseline之差当作优势函数
A
θ
A^\theta
Aθ。
2. From on-policy to off-policy
2.1 On-Policy and Off-Policy
- On-Policy:策略从自己与环境交互采样的轨迹中学习。
- off-Policy:策略从其他策略与环境交互采样的轨迹中学习。

上文提到过策略梯度的模型优化过程,首先利用当前策略采样获得大量轨迹,然后根据轨迹计算梯度优化模型参数。因为每一轮策略模型更新后,采样获得的轨迹分布发生变化,所以上一轮采样的历史轨迹不能重用。很明显这是一种On-Policy方法。为了更加有效的利用数据,我们需要思考如何才能使用到历史经验,也就是将On-Policy策略转化为Off-Policy策略。
2.2 Important Sampling
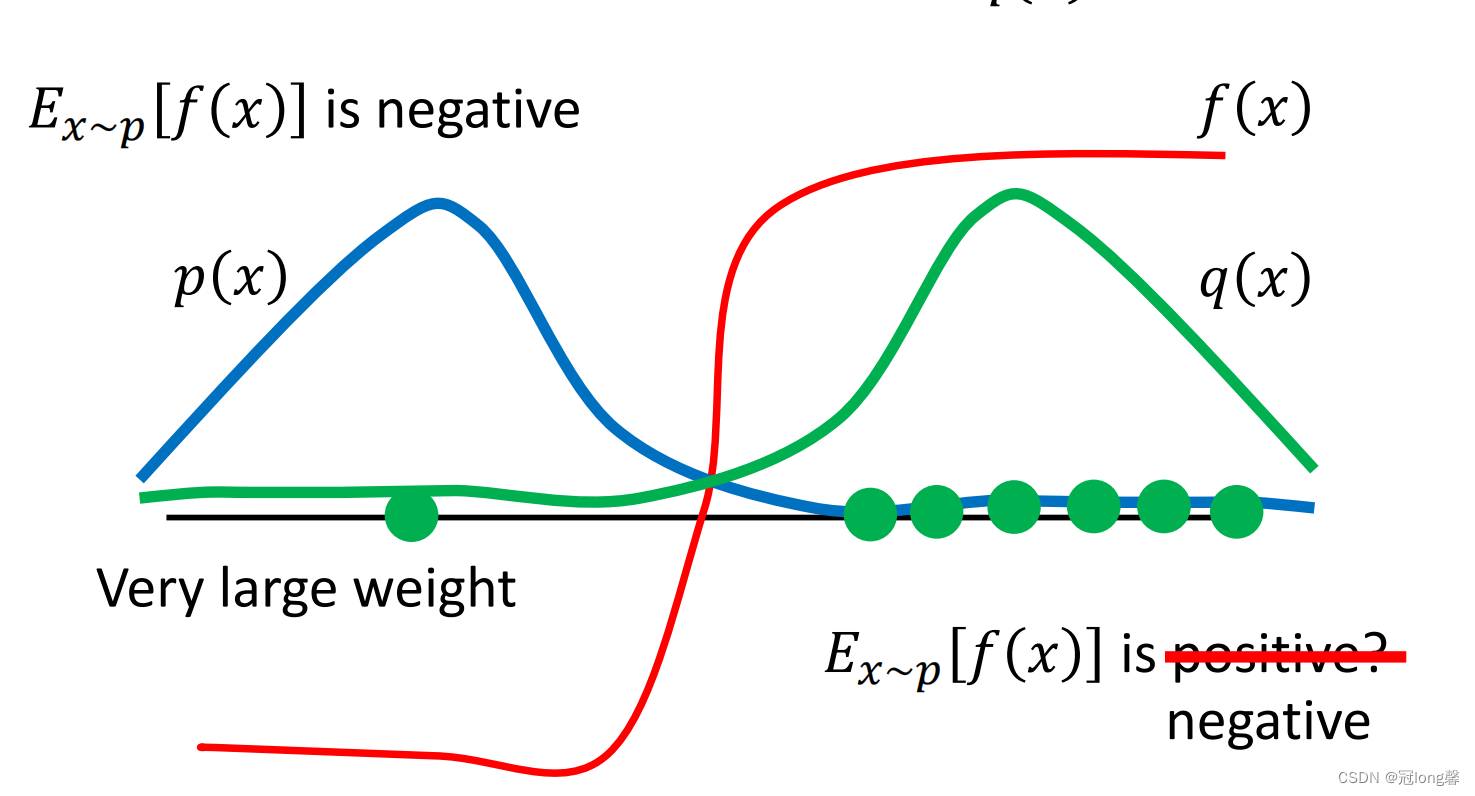
幸运的是我们可以使用重要性采样来改变采样数据的分布,这样我们就可以实现从其他策略采样获得的轨迹中学习了。
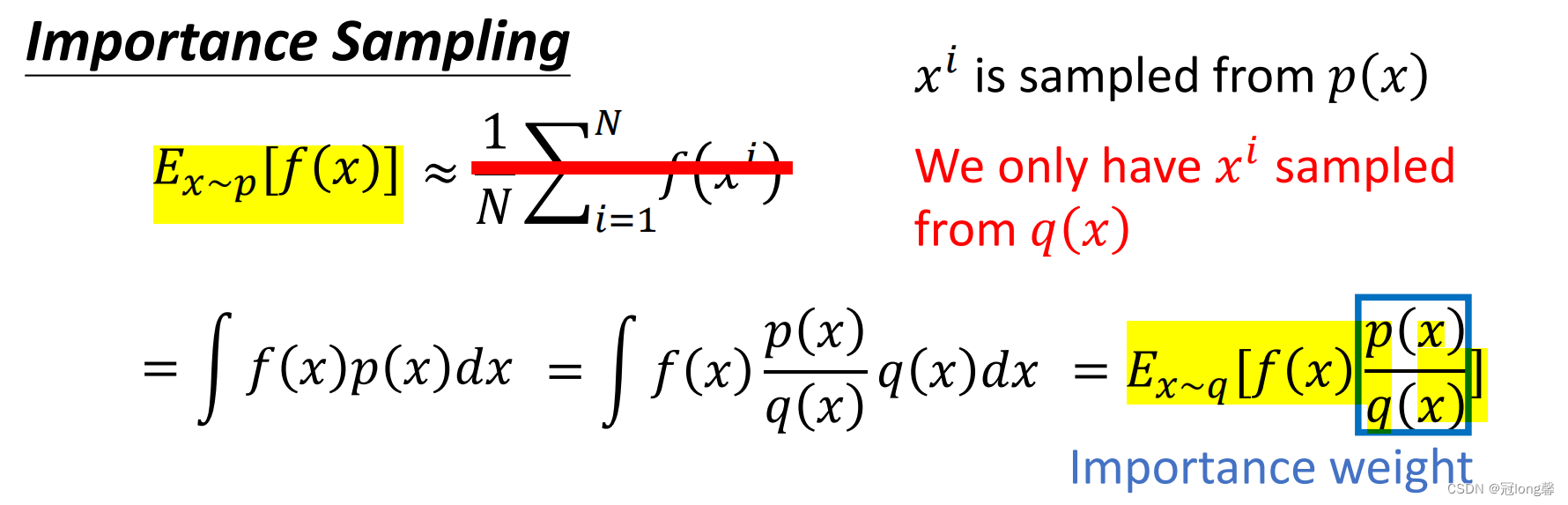
这看上去是个完美的方案,使用重要性权重可以使两种采样数据的均值相等。但是任意两种分布
p
(
x
)
,
q
(
x
)
p(x),q(x)
p(x),q(x)都可以很好的实现转换吗?
2.2.1 Issue
我们思考采用两种策略采样获得数据的方差,如下图所示:
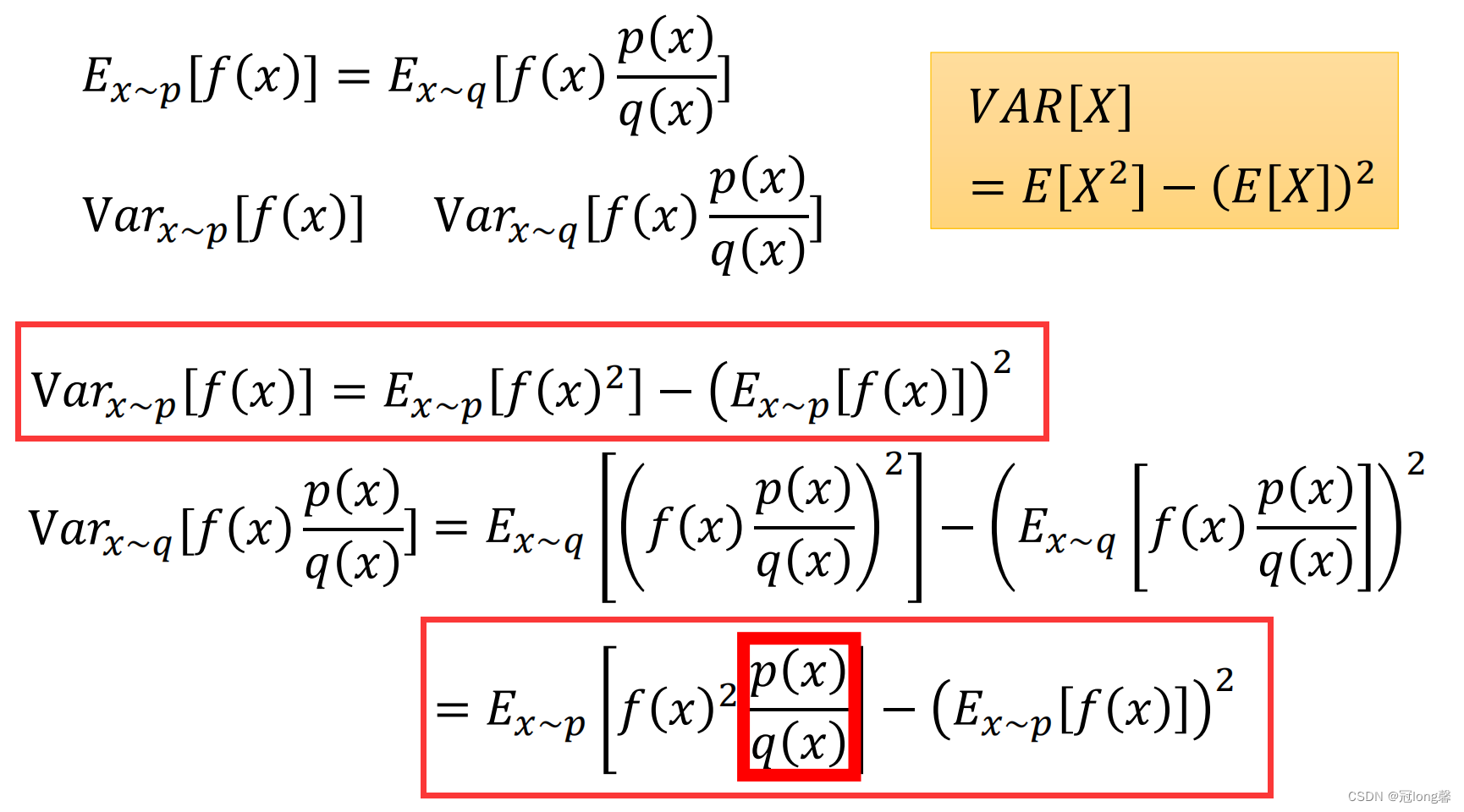
很明显我们可以看出
p
(
x
)
,
q
(
x
)
p(x),q(x)
p(x),q(x)的差距不能太大,否则即使经过重要性采样转换后,所采集的数据的方差仍然具有较大差距。
2.3 Off-Policy –> On-Policy
使用重要性采样,我们可以根据历史经验计算策略梯度

结合上文提到的Baseline与Credit优化机制,我们的策略梯度和目标函数如下图所示:

我们可以思考,在将On-Policy策略转化为Off-Policy策略时我们如何保证两种策略采样分布差距不要过大。也许我们可以加上约束条件(TRPO),或者直接在奖励函数中增加限制(PPO)。
3. PPO/TRPO
3.1 TRPO
在2.3的基础上增加了限制条件,来保证两种策略分布不能差距太大。但是因为有限制条件,TRPO在实际处理时并不容易。

3.2 PPO

理解: 在目标函数中增加了两种策略采样分布的距离(采集到的(s,a)对的距离),希望通过减小KL也就是分布差距实现在优化的同时两种分布不要差距过大。
3.3 PPO2
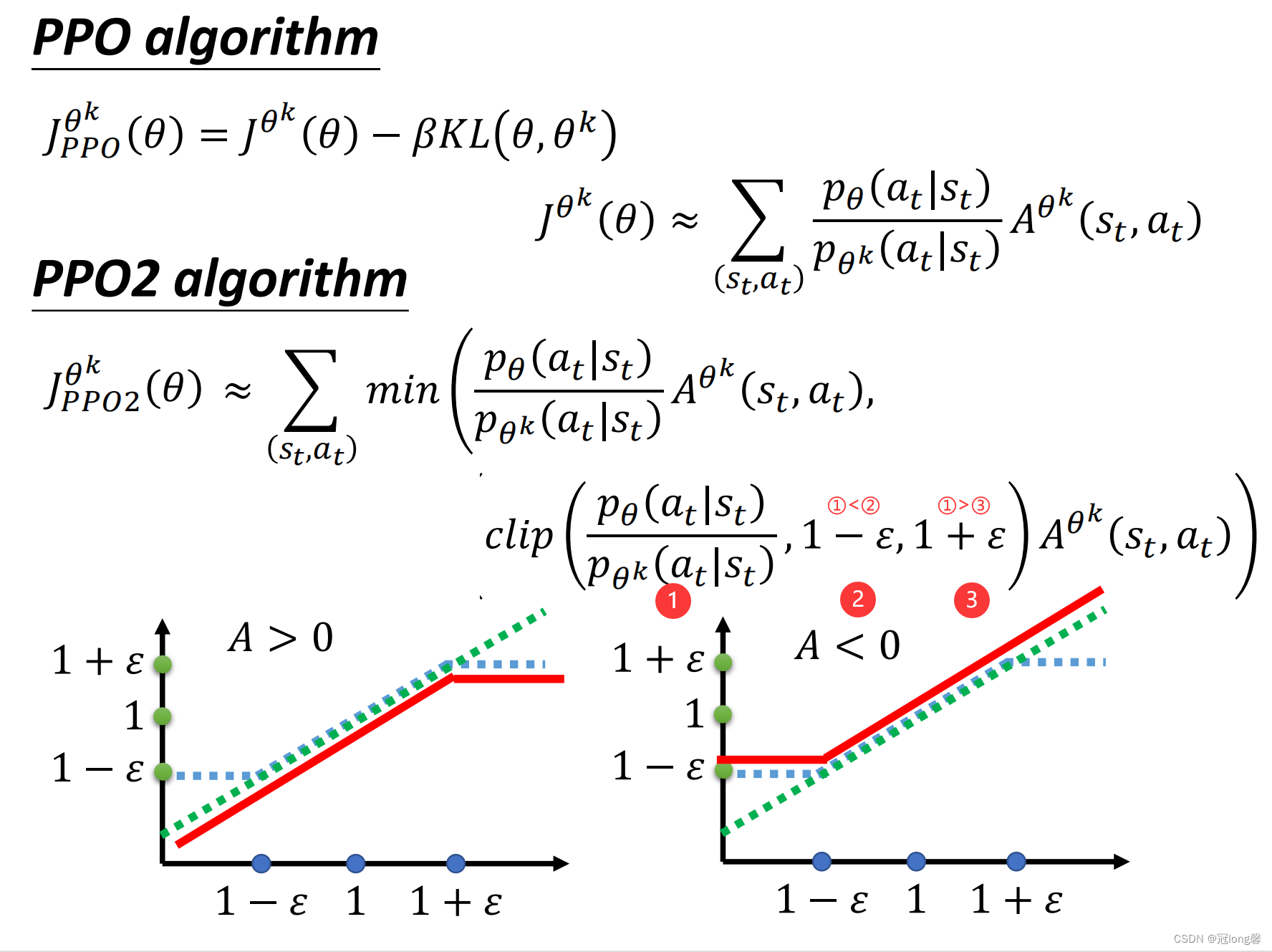
理解: 当分布差距比较小可以直接使用重要性采样修正,当差距较大时使用固定值修正。