Hamilton

该种方法复杂度较高

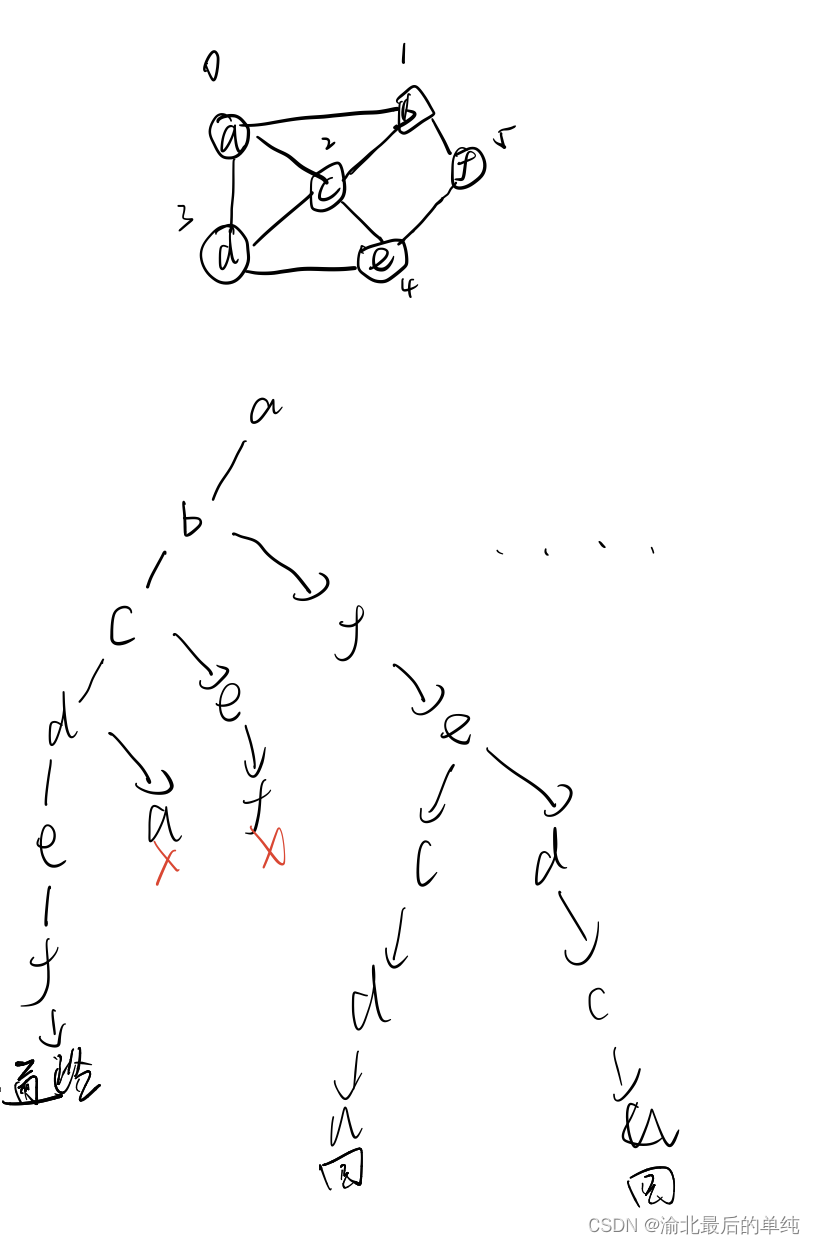
思路：

dfs + 回溯

相当于就是以树状的形式 举出 每种可能 。

以下举例部分 情况 以及 代码。

具体思路详见代码。

import java.util.Arrays;

public class Hamiton {

    public void getHamiltonCircuit(int[][] adjMatrix) {
        boolean[] isVisited = new boolean[adjMatrix.length];       //用于标记图中顶点是否被访问
        int[] path = new int[adjMatrix.length];       //记录哈密顿回路路径
        Arrays.fill(isVisited,false);
        Arrays.fill(path,-1);
        isVisited[0] = true;
        path[0] = 0; //从 第一个节点开始 , 选取出发节dian
        dfs(adjMatrix, path, isVisited, 1);     //dfs查找哈密顿回路
    }
    public boolean dfs(int[][] adjMatrix, int[] path, boolean[] isVisited, int step) {
        if(step == adjMatrix.length) {     //当已经遍历完图中所有顶点
            if(adjMatrix[path[step - 1]][0] == 1) { // 递归 结束条件 最后一个节点能够回到 第一个节点 输出 路径
                System.out.println("哈密顿图");
                for (int i = 0; i < path.length; i++)
                    System.out.print(((char) (path[i] + 'a')) + "——>");
                System.out.print(((char) (path[0] + 'a')));
                System.out.println();
                return false;
            }else{ //  哈密顿通路
                System.out.println("半哈密顿图");
                for (int i = 0; i < path.length - 1; i++)
                    System.out.print(((char) (path[i] + 'a')) + "——>");
                System.out.println((char) (path[path.length - 1] + 'a'));
                return false;
            }
        } else {
            for(int i = 0;i < adjMatrix.length;i++) {
                if(!isVisited[i] && adjMatrix[path[step - 1]][i] == 1) {
                    isVisited[i] = true; // 标记访问过该节点
                    path[step] = i;
                    if(dfs(adjMatrix, path, isVisited, step + 1))
                        return true;
                    else {
                        isVisited[i] = false;    //回溯
                        path[step] = -1;
                    }
                }
            }
        }
        return false;
    }

    public static void main(String[] args) {
        Hamiton test = new Hamiton();
        // 示例矩阵
        int[][] adjMatrix = {
                {-1,1,1,1,-1,-1},
                {1,-1,1,-1,-1,1},
                {1,1,-1,1,1,-1},
                {1,-1,1,-1,1,-1},
                {-1,-1,1,1,-1,1},
                {-1,1,-1,-1,1,-1}
        };
        test.getHamiltonCircuit(adjMatrix);
        task(test);
    }
    //  12.24 作业演示
    public static void task(Hamiton test){
        int[][] a ={
                {-1,1,-1,-1,-1,-1,-1},
                {-1,-1,1,-1,1,-1,-1},
                {-1,1,-1,1,1,-1,-1},
                {-1,-1,1,-1,1,-1,-1},
                {-1,1,1,1,-1,1,-1},
                {-1,-1,-1,-1,1,-1,-1},
                {-1,-1,1,-1,-1,-1,-1},
        };
        System.out.println("ans : ");
        test.getHamiltonCircuit(a);

        int[][] b = new int[11][11];
        int[][] routes =  {
                {0,1},
                {0,3},
                {0,4},
                {0,6},
                {1,2},
                {1,7},
                {2,5},
                {2,3},
                {3,8},
                {3,10},
                {4,5},
                {4,9},
                {5,6},
                {5,7},
                {5,8},
                {6,10},
                {7,10},
                {8,9},
                {9,10}
        };
        init(b,routes);
        System.out.println("ans : ");
        test.getHamiltonCircuit(b);
    }

    public static void init(int[][] martrix,int[][] routes) {
        for(int[] arr : routes){
            martrix[arr[0]][arr[1]] = 1;
            martrix[arr[1]][arr[0]] = 1;
        }
    }
    
}

半哈密顿图
a——>b——>c——>d——>e——>f
哈密顿图
a——>b——>f——>e——>c——>d——>a
哈密顿图
a——>b——>f——>e——>d——>c——>a
哈密顿图
a——>c——>b——>f——>e——>d——>a
哈密顿图
a——>c——>d——>e——>f——>b——>a
半哈密顿图
a——>d——>c——>b——>f——>e
哈密顿图
a——>d——>c——>e——>f——>b——>a
半哈密顿图
a——>d——>e——>c——>b——>f
哈密顿图
a——>d——>e——>f——>b——>c——>a

我是菜鸡，这应该是最简单的查找方法 复杂度 极高 ，更高深的详见百度。

12.23日作业 运行示例 结果

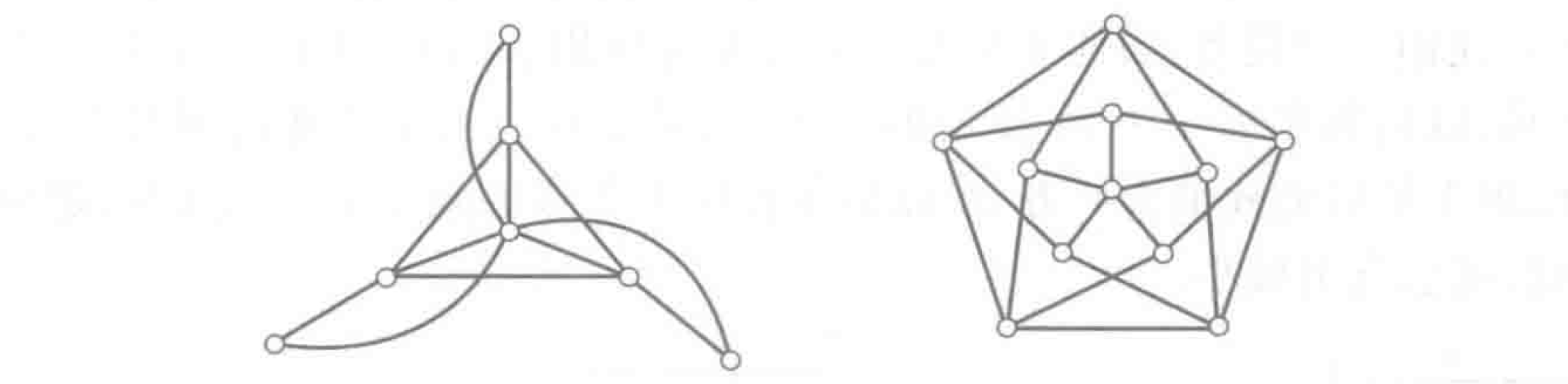
(a):

(b):