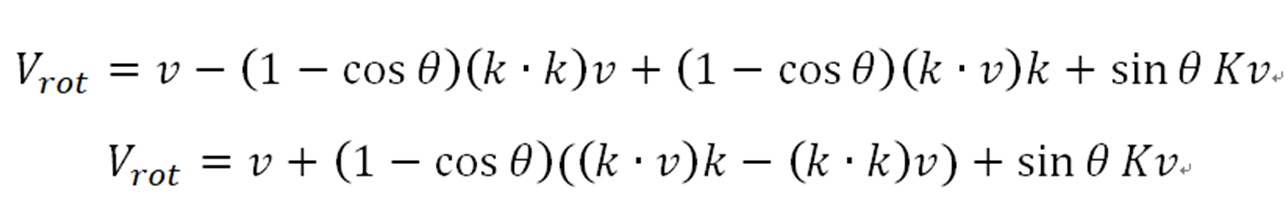转载于:https://blog.csdn.net/qq_22235957/article/details/80461290
旋转向量中V的单位向量代表方向,模代表角度,通过罗德里格斯方程可以将旋转向量转换成旋转矩阵。
罗德里格斯旋转方程是从角度和向量计算出相应的旋转矩阵,这个旋转方程在很多方面有重要的应用,这里简要概述一下方程的推导过程。
主要参考资料是维基百科,其实基本上就是翻译一下,自己走一遍这个推导过程,这里把链接贴出来。
推导过程:
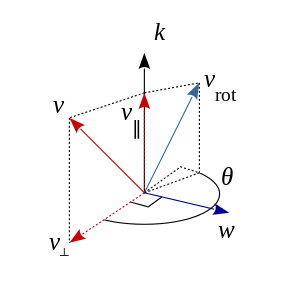
整个推导过程都是围绕上面的图片开展的,进行向量推导。
首先,定义向量k是旋转轴的单位矢量,向量v是绕向量k旋转角度θ的任意向量(旋转方向遵循右手定则,图中逆时针)。
使用点乘和叉乘,向量v可以分解成与轴k平行和垂直的分量,

与k平行的分量是

向量v在k上的向量投影,垂直于k的分量为

矢量k×v可以看作是v⊥绕k逆时针旋转90°的副本,所以它们的大小相等,但是方向是垂直的。同样,向量k×(k×v)是v⊥绕k逆时针旋转180°的副本,使得k×(k×v)和v⊥的大小相等,但方向相反(因此符号相反)。
矢量三重叉积链接了平行分量和垂直分量,参考公式为a×(b×c)=(a·c)b – (a·b)c ,对于给定任意三个向量a,b,c。
平行于轴的分量在旋转时不会改变幅度和方向,

根据以上分析,垂直分量在旋转时会改变方向,但保持其大小

并且由于k和v||是平行的,所以它们的叉积是零 k×v|| = 0,因此

因此

这种旋转是正确的,因为矢量v⊥和k×v具有相同的长度,并且k×v是v⊥围绕k逆时针旋转90°。使用三角函数正弦和余弦对v⊥和k×v进行适当乘积可以得到旋转的垂直分量。旋转分量的形式类似于笛卡尔基的2D平面极坐标(r,θ)中的径向向量

其中ex,ey是它们指示方向上的单位向量。
现在完整的旋转矢量是

用上述结果中的v ||rot和v⊥rot的定义代替

矩阵表示:
将v和k×v表示为列矩阵,叉积可以表示为矩阵乘积

令矩阵K表示单位向量k的“叉积矩阵”

矩阵方程可以表示为

对于任何向量v(实际上,矩阵K是具有特征值0和±i)。

而且,由于k是单位向量,所以k具有单位2-范数。 因此旋转公式(1-10)可以表示为

补充一下推导过程:(1-10)到(1-15)都点跨度比较大,其实中间经过了下面一个步骤,
再根据矢量三重叉积就可以获得(1-15)。
将v用紧凑表达式表达

最后获得罗德里格斯旋转方程: