1. 先看效果
参考源码: https://github.com/andyzeng/tsdf-fusion-python

从图中可以看出,tsdf算法的重建效果还是不错的.该算法是很多牛掰3D重建算法的基础,例如:KinectFusion、InfiniTAM等.
2. 原理解析
2.1 体素栅格建立
根据环境待重建点云分布情况,确定包围所有点云的边界大小,然后再将边界内的空间根据设定的尺寸大小进行体素化,这样就将空间划分成一个个下图所示的小立方体(立方体的尺寸由用户自行定义,越小建模精度越高,越耗时),图像来源https://blog.csdn.net/qq_30339595/article/details/86103576
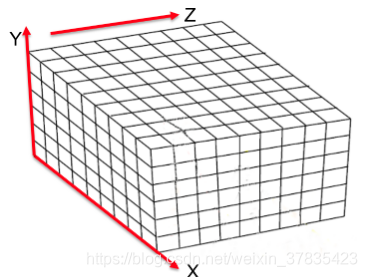
2.2 体素栅格更新
定义2.1节建立的体素栅格所在的坐标系为世界坐标系,体素坐标为
(
p
0
w
,
p
1
w
,
.
.
.
,
p
m
w
)
(\mathbf{p}_{0}^{w}, \mathbf{p}_{1}^{w}, …,\mathbf{p}_{m}^{w})
(p0w,p1w,...,pmw),相机的位姿为
(
T
c
0
w
,
T
c
1
w
.
.
.
,
T
c
n
w
)
(\mathbf{T}_{c_{0}}^{w}, \mathbf{T}_{c_{1}}^{w} …, \mathbf{T}_{c_{n}}^{w})
(Tc0w,Tc1w...,Tcnw),相机的内参为
K
\mathbf{K}
K
2.2.1 投影世界坐标系下的体素栅格到图像坐标系
I
i
j
=
[
u
i
j
v
i
j
]
=
K
T
c
i
w
p
j
w
(1)
\mathbf{I}_{ij} = \begin{bmatrix}\mathbf{u}_{ij} \\ \mathbf{v}_{ij}\end{bmatrix} = \mathbf{K}\mathbf{T}_{c_{i}}^{w}\mathbf{p}_{j}^{w} \tag{1}
Iij=[uijvij]=KTciwpjw(1)
式中
i
∈
(
0
,
1
,
.
.
.
.
,
n
)
i\in(0, 1, …., n)
i∈(0,1,....,n),
j
∈
(
0
,
1
,
.
.
.
,
m
)
j\in(0, 1, …, m)
j∈(0,1,...,m).
2.2.2 更新栅格tsdf值及对应的权重
首先计算每个体素sdf值:
s
d
f
j
=
∥
t
p
j
w
−
t
c
i
w
∥
−
d
e
p
(
I
i
j
)
(2)
sdf_{j} = \left \| \mathbf{t}_{pj}^{w} – \mathbf{t}_{ci}^{w} \right \| – \mathbf{dep}(\mathbf{I}_{ij}) \tag{2}
sdfj=∥∥tpjw−tciw∥∥−dep(Iij)(2)
式中
t
p
j
w
\mathbf{t}_{pj}^{w}
tpjw表示第
j
j
j个体素在世界坐标系下的位置信息,
t
c
i
w
\mathbf{t}_{ci}^{w}
tciw表示第
i
i
i个相机位姿在世界坐标系下的位置信息,
d
e
p
(
I
i
j
)
\mathbf{dep}(\mathbf{I}_{ij})
dep(Iij)表示第
j
j
j个体素在第
i
i
i个相机深度图像坐标系下的深度值.
截断每个体素的sdf值:
i
f
s
d
f
j
>
0
t
s
d
f
j
=
m
i
n
(
1
,
s
d
f
j
/
t
r
u
n
c
)
e
l
s
e
t
s
d
f
j
=
m
a
x
(
−
1
,
s
d
f
j
/
t
r
u
n
c
)
(3)
\begin{aligned} &if sdf_{j} > 0 tsdf_{j} = min(1, sdf_{j}/trunc) \\ &else tsdf_{j} = max(-1, sdf_{j}/trunc) \end{aligned} \tag{3}
if sdfj>0 tsdfj=min(1,sdfj/trunc)else tsdfj=max(−1,sdfj/trunc)(3)
式中
t
r
u
n
c
trunc
trunc 表示截断距离,人为设定,可理解为相机深度信息的误差值,如果误差越大,建议该值设置大一些,否则会丢掉很多深度相机获取的信息.
计算每个体素的tsdf值:
t
s
d
f
j
=
t
s
d
f
j
−
1
⋅
w
j
−
1
+
t
s
d
f
j
⋅
w
j
w
j
−
1
+
w
j
(4)
tsdf_{j} = \frac{tsdf_{j-1}\cdot w_{j-1} + tsdf_{j}\cdot w_{j}}{w_{j-1}+w_{j}} \tag{4}
tsdfj=wj−1+wjtsdfj−1⋅wj−1+tsdfj⋅wj(4)
式中初始
w
j
w_{j}
wj一般默认设置为1.
计算每个体素的权值:
w
j
=
w
j
−
1
+
w
j
(5)
w_{j} = w_{j-1} + w_{j} \tag{5}
wj=wj−1+wj(5)
2.3 找等值面
通过2.2节更新完每个体素的tsdf值之后,通过marching cubes算法寻找体素中的等值面作为重构曲面,算法示意图如下:
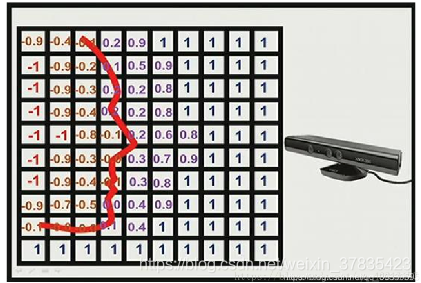
其中每个栅格里面的值为对应体素的tsdf值.
3. 源码解析
参考源码: https://github.com/andyzeng/tsdf-fusion-python
注: 这里仅分析cpu版本源码,对于深入理解tsdf原理足够.
3.1 体素栅格建立
def __init__(self, vol_bnds, voxel_size, use_gpu=True):
# 将点云分布边界转换成numpy数组
vol_bnds = np.asarray(vol_bnds)
assert vol_bnds.shape == (3, 2), "[!] `vol_bnds` should be of shape (3, 2)."
# 定义体素体参数
self._vol_bnds = vol_bnds # 体素体边界
self._voxel_size = float(voxel_size) # 体素体每个立方体边长
self._trunc_margin = 5 * self._voxel_size # truncation on SDF # 截断距离,设置为体素边长的5倍
self._color_const = 256 * 256 # 辅助参数,用于提取rgb值
# 调整体素体边界确保c连续
self._vol_dim = np.ceil((self._vol_bnds[:,1]-self._vol_bnds[:,0])/self._voxel_size).copy(order='C').astype(int) # 计算体素体每个维度方向上的栅格数量
self._vol_bnds[:,1] = self._vol_bnds[:,0]+self._vol_dim*self._voxel_size # 根据各个维度栅格数量,计算体素体边界
self._vol_origin = self._vol_bnds[:,0].copy(order='C').astype(np.float32) # 使体素体原点为c有序
# 初始化保存体素体信息的容器
self._tsdf_vol_cpu = np.ones(self._vol_dim).astype(np.float32) # 用于保存每个体素栅格的tsdf值
self._weight_vol_cpu = np.zeros(self._vol_dim).astype(np.float32) # 用于保存每个体素栅格的权重值
self._color_vol_cpu = np.zeros(self._vol_dim).astype(np.float32) # 用于保存每个体素栅格的颜色值(将rgb三个值压缩成一个float32值表示)
# 获取每个体素栅格的坐标
xv, yv, zv = np.meshgrid(
range(self._vol_dim[0]),
range(self._vol_dim[1]),
range(self._vol_dim[2]),
indexing='ij'
)
self.vox_coords = np.concatenate([
xv.reshape(1,-1),
yv.reshape(1,-1),
zv.reshape(1,-1)
], axis=0).astype(int).T
3.2 体素栅格更新
def integrate(self, color_im, depth_im, cam_intr, cam_pose, obs_weight=1.):
im_h, im_w = depth_im.shape # 获取图像尺寸
# 将rgb三个值表示的颜色通道信息转换成一个用float32表示的单通道信息
color_im = color_im.astype(np.float32)
color_im = np.floor(color_im[...,2]*self._color_const + color_im[...,1]*256 + color_im[...,0])
# 将体素栅格坐标转换成像素坐标,对应2.2节的公式(1)
cam_pts = self.vox2world(self._vol_origin, self.vox_coords, self._voxel_size) # 体素坐标系转换到世界坐标系
cam_pts = rigid_transform(cam_pts, np.linalg.inv(cam_pose)) # 世界坐标系转换到相机坐标系
pix_z = cam_pts[:, 2]
pix = self.cam2pix(cam_pts, cam_intr) # 相机坐标系转换到像素坐标系
pix_x, pix_y = pix[:, 0], pix[:, 1]
# 移除像素边界之外的投影点
valid_pix = np.logical_and(pix_x >= 0,
np.logical_and(pix_x < im_w,
np.logical_and(pix_y >= 0,
np.logical_and(pix_y < im_h,
pix_z > 0))))
depth_val = np.zeros(pix_x.shape)
depth_val[valid_pix] = depth_im[pix_y[valid_pix], pix_x[valid_pix]]
# 更新每个体素栅格的tsdf值及对应的权重
depth_diff = depth_val - pix_z # 计算sdf值,对应公式(2)
valid_pts = np.logical_and(depth_val > 0, depth_diff >= -self._trunc_margin) # 确定出有效深度值(即sdf值的值要大于负的截断值)
dist = np.minimum(1, depth_diff / self._trunc_margin) # 计算截断值,对应公式(3)
valid_vox_x = self.vox_coords[valid_pts, 0]
valid_vox_y = self.vox_coords[valid_pts, 1]
valid_vox_z = self.vox_coords[valid_pts, 2]
w_old = self._weight_vol_cpu[valid_vox_x, valid_vox_y, valid_vox_z] # 提取上个循环对应体素的权重,对应公式(4)中的w_j_1
tsdf_vals = self._tsdf_vol_cpu[valid_vox_x, valid_vox_y, valid_vox_z] # 提取上个循环对应的tsdf值,对应公式(4)中的tsdf_j_1
valid_dist = dist[valid_pts]
tsdf_vol_new, w_new = self.integrate_tsdf(tsdf_vals, valid_dist, w_old, obs_weight) # 计算体素新的权重和tsdf值,对应公式(4)(5)
self._weight_vol_cpu[valid_vox_x, valid_vox_y, valid_vox_z] = w_new # 将新的权值和tsdf值更新到体素信息容器中
self._tsdf_vol_cpu[valid_vox_x, valid_vox_y, valid_vox_z] = tsdf_vol_new
# 更新每个体素栅格的颜色值,其实就是按旧的权重和新的权重加权更新每个体素栅格的rgb值
old_color = self._color_vol_cpu[valid_vox_x, valid_vox_y, valid_vox_z]
old_b = np.floor(old_color / self._color_const)
old_g = np.floor((old_color-old_b*self._color_const)/256)
old_r = old_color - old_b*self._color_const - old_g*256
new_color = color_im[pix_y[valid_pts],pix_x[valid_pts]]
new_b = np.floor(new_color / self._color_const)
new_g = np.floor((new_color - new_b*self._color_const) /256)
new_r = new_color - new_b*self._color_const - new_g*256
new_b = np.minimum(255., np.round((w_old*old_b + obs_weight*new_b) / w_new))
new_g = np.minimum(255., np.round((w_old*old_g + obs_weight*new_g) / w_new))
new_r = np.minimum(255., np.round((w_old*old_r + obs_weight*new_r) / w_new))
self._color_vol_cpu[valid_vox_x, valid_vox_y, valid_vox_z] = new_b*self._color_const + new_g*256 + new_r
3.3 找等值面
def get_mesh(self):
# 获取体素栅格的tsdf值及对应的颜色值
tsdf_vol, color_vol = self.get_volume()
# 直接使用scikit-image工具包中封装的Marching cubes算法接口提取等值面
verts, faces, norms, vals = measure.marching_cubes_lewiner(tsdf_vol, level=0)
verts_ind = np.round(verts).astype(int)
verts = verts*self._voxel_size+self._vol_origin # voxel grid coordinates to world coordinates
# 为每个体素赋值颜色
rgb_vals = color_vol[verts_ind[:,0], verts_ind[:,1], verts_ind[:,2]]
colors_b = np.floor(rgb_vals/self._color_const)
colors_g = np.floor((rgb_vals-colors_b*self._color_const)/256)
colors_r = rgb_vals-colors_b*self._color_const-colors_g*256
colors = np.floor(np.asarray([colors_r,colors_g,colors_b])).T
colors = colors.astype(np.uint8)
return verts, faces, norms, colors