Speeded Up Robust Features(SURF,加速稳健特征),是一种稳健的局部特征点检测和描述算法。
与Sift算法一样,Surf算法的基本路程可以分为三大部分:局部特征点的提取、特征点的描述、特征点的匹配。
SURF的算法原理如下:
1.构建Hessian矩阵构造高斯金字塔尺度空间
事实上surf构造的金字塔图像与sift有非常大不同,就是由于这些不同才加快了其检測的速度。Sift採用的是DOG图像。而surf採用的是Hessian矩阵行列式近似值图像。Hessian矩阵是Surf算法的核心。
对一个图像f(x,y),其Hessian矩阵如下:
即每个像素点都能够求出一个Hessian矩阵。
H矩阵判别式为:
判别式的值是H矩阵的特征值。能够利用判定结果的符号将全部点分类。依据判别式取值正负,来判别该点是或不是极值点。
因为我们的特征点须要具备尺度无关性,所以在进行Hessian矩阵构造前,须要对其进行高斯滤波。
在SURF算法中,图像像素l(x,y)即为函数值f(x,y),选用二阶标准高斯函数作为滤波器,通过特定核间的卷积计算二阶偏导数,这样便能计算出H矩阵的三个矩阵元素L_xx,L_xy,L_yy 从而计算出H矩阵:
这样,经过滤波后再进行Hessian的计算,其公式如下:
L(x,t)是一幅图像在不同解析度下的表示,利用高斯核G(t)与图像函数 I(x) 在点x的卷积来实现。其中高斯核G(t):
g(x)为高斯函数,t为高斯方差。通过这样的方法能够为图像中每一个像素计算出其H行列式的决定值,并用这个值来判别特征点。为方便应用。Herbert Bay提出用近似值现取代L(x,t)。为平衡准确值与近似值间的误差引入权值叫,权值随尺度变化。则H矩阵判别式可表示为:
Hessian矩阵判别式中的f(x,y)是原始图像的高斯卷积,由于高斯核实服从正态分布的,从中心点往外,系数越来越低,为了提高运算速度,Surf使用了盒式滤波器来近似替代高斯滤波器,所以在Dxy上乘了一个加权系数0.9,目的是为了平衡因使用盒式滤波器近似所带来的误差。
2.尺度空间
高斯滤波器和盒式滤波器的示意图如下:
盒式滤波器可以提高运算速度,涉及到积分图的使用。盒式滤波器对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题,这正是积分图的强项,只需要简单几次查找积分图就可以完成。
同Sift一样,Surf的尺度空间也是由O组L成组成。不同的是,Sift中下一组图像的尺寸是上一组的一半,同一组间图像尺寸一样,但是所使用的高斯模糊系数逐渐增大;而在Surf中,不同组间图像的尺寸都是一致的,但不同组间使用的盒式滤波器的模板尺寸逐渐增大,同一组间不同层间使用相同尺寸的滤波器,但是滤波器的模糊系数逐渐增大。
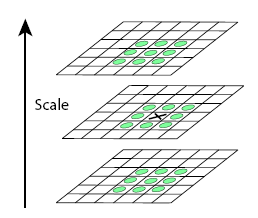
3.特征点定位
特征点的定位过程Surf和Sift保持一致,将经过Hessian矩阵处理的每个像素点与二维图像空间和尺度空间邻域内的26个点进行比较,初步定位出关键点,再经过滤除能量比较弱的关键点以及错误定位的关键点,筛选出最终的稳定的特征点。
4. 特征点主方向分配
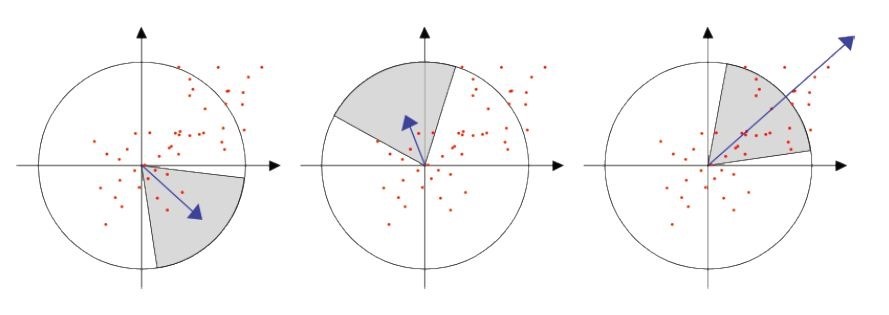
Sift特征点方向分配是采用在特征点邻域内统计其梯度直方图,取直方图bin值最大的以及超过最大bin值80%的那些方向作为特征点的主方向。而在Surf中,采用的是统计特征点圆形邻域内的harr小波特征。即在特征点的圆形邻域内,统计60度扇形内所有点的水平、垂直harr小波特征总和,然后扇形以0.2弧度大小的间隔进行旋转并再次统计该区域内harr小波特征值之后,最后将值最大的那个扇形的方向作为该特征点的主方向。
该过程的示意图例如以下:
5. 生成特征点描述子
在Sift中,是取特征点周围4*4个区域块,统计每小块内8个梯度方向,用着4*4*8=128维向量作为Sift特征的描述子。
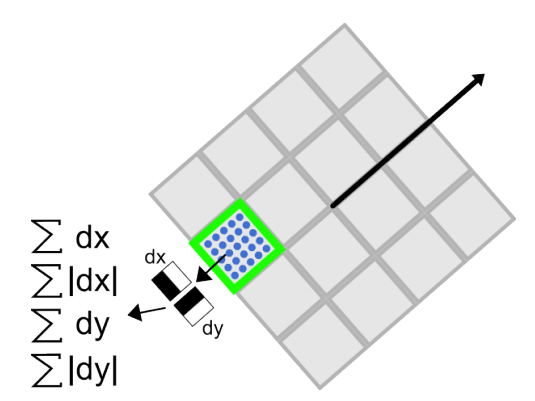
在surf中,也是在特征点周围取一个正方形框,框的边长为20s(s是所检測到该特征点所在的尺度)。该框带方向。方向当然就是第4步检測出来的主方向了。然后把该框分为16个子区域。每一个子区域统计25个像素的水平方向和垂直方向的haar小波特征,这里的水平和垂直方向都是相对主方向而言的。该haar小波特征为水平方向值之和,水平方向绝对值之和,垂直方向之和,垂直方向绝对值之和。该过程的示意图例如以下所看到的:
这样每一个小区域就有4个值,所以每一个特征点就是16*4=64维的向量。相比sift而言,少了一半。这在特征匹配过程中会大大加快匹配速度。
6.特征点匹配
与Sift特征点匹配类似,Surf也是通过计算两个特征点间的欧式距离来确定匹配度,欧氏距离越短,代表两个特征点的匹配度越好。不同的是Surf还加入了Hessian矩阵迹的判断,如果两个特征点的矩阵迹正负号相同,代表这两个特征具有相同方向上的对比度变化,如果不同,说明这两个特征点的对比度变化方向是相反的,即使欧氏距离为0,也直接予以排除。

![gif[1]](https://images0.cnblogs.com/blog/522070/201503/241724437708705.gif)
![gif[2]](https://images0.cnblogs.com/blog/522070/201503/241724446771148.gif)
![gif[4]](https://images0.cnblogs.com/blog/522070/201503/241724461309391.gif)