JavaScript 链表：判断链表是否有环【两种方法，思路与知识点总结】

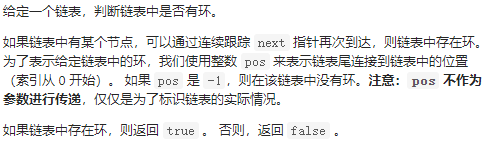
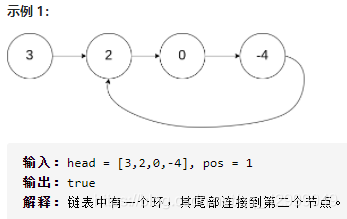
思路一：一个走两步，一个走一步，如果链表中有环，必会相遇。

function hasCycle(head) {
    let one=head;
    let two=head;
    while(two!=null&&two.next!=null){
        one=one.next;
        two=two.next.next;
        if(one===two){
            return true;
        }
    }
    return false;
}

思路二：遍历链表中的每个节点，并将保存到set，如果下次遇到了遍历过的节点，说明链表中存在环，此时的节点为入环节点。
时间复杂度O(n) 空间复杂度O(n)

function hasCycle(head) {
    const visited = new Set();
    while (head !== null) {
        if (visited.has(head)) {
            return true;
        } else {
            visited.add(head);
            head = head.next;
        }
    }
    return false;
}

此题返回的不是布尔值而是入环节点

思路一：遍历链表中的每个节点，并将保存到set，如果下次遇到了遍历过的节点，说明链表中存在环，此时的节点为入环节点。
时间复杂度O(n) 空间复杂度O(n)

function detectCycle1(head) {
    const visited = new Set();
    while (head !== null) {
        if (visited.has(head)) {
            return head; // 有环，此时的节点为入环节点
        } else {
            visited.add(head);
            head = head.next;
        }
    }
    return null;
}

思路二：快慢指针
快慢指针，快慢指针同时从头节点一起走，如果链表有环，当快慢指针第一次相遇时，只需要将其中一个指针移动到链表头部，另一个指针保持在相遇的位置不变，两个指针再同时出发，每次只走一步，再次相遇时的节点则为环的入口节点。

当快慢指针第一次相遇时，
慢指针移动的距离为 s1 = A + B + n1 * L
快指针移动的距离为 s2 = A + B + n2 * L
快指针的速度是慢指针的两倍，所以 s2 = 2* s1，即A + B + n2 * L = 2A + 2B + n1 * L 即 A = (n2 – n1) * L – B，表示A的距离=n圈环的周长 – B的距离
所以即在第一次相遇点，把其中一个指针指向链表头节点，一个在相遇节点，此时两个指针一起走，那肯定会在入环节点相遇

//注释版代码
function detectCycle3(head) {
    // 快慢指针指向头节点
    let fast = head;
    let slow = head; 

    while (fast && fast.next) {
        fast = fast.next.next;
        slow = slow.next;

        // 第1次相遇
        if (fast == slow) {
            // console.log(`相遇节点值是：${slow.val}`);
            // 其中一个指针指向不动，另一个指针指向头
            slow = head;

            while (fast !== slow) {
                // 快慢指针都同时只移动一步
                slow = slow.next;
                fast = fast.next;
            }
            // 此时第2次相遇，指向的那个节点就是入环节点
            return slow;
        }
    }
    return null;
}

//简洁版代码
function detectCycle3(head) {
    let fast = head;
    let slow = head; 
    while (fast && fast.next) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) {
            slow = head;
            while (fast !== slow) {
                slow = slow.next;
                fast = fast.next;
            }
            return slow;
        }
    }
    return null;
}