Genetic algorithms (GA) are an optimization and search technique based on the principles of genetics and natural selection, in essence mimicking the natural evolution process that we observe in life. Their general principle is based on the concept of having an initial population composed of several individuals — with each representing a particular solution to the problem — and allow it to evolve to a state that maximizes its overall fitness, using three main operators: selection, crossover and mutation. We’ll look into these aspects a bit more in detail below.

遗传算法(GA)是一种基于遗传和自然选择原理的优化和搜索技术，实质上模仿了我们在生活中观察到的自然进化过程。 他们的一般原则基于以下概念： 初始人口由几个人组成，每个人代表一个特定的问题解决方案，并使用三个主要运算符将其发展为最大化整体适应性的状态： 选择 ， 交叉和突变 。 我们将在下面更加详细地研究这些方面。

Genetic Algorithms are nothing short of fantastic, as they can be applied to many kinds of optimization problems and find solutions to complex functions for which we do not have a mathematical expression. This comes at a cost of computational complexity though, as, for large populations, we’ll have to evaluate the fitness of all individuals at every generation. If the fitness function is expensive, the algorithm run will be slow.

遗传算法简直就是太神奇了，因为它们可以应用于多种优化问题并找到我们没有数学表达式的复杂函数的解。 但是，这是以计算复杂性为代价的，因为对于大量人口，我们必须评估每一代所有个体的适应性。 如果适应度函数昂贵，则算法运行会很慢。

GA’s can be divided into Binary and Continuous, depending on the type of problem we’re optimizing for. Potentially all problems could be broken down as having their variables (genes) represented by binary strings, but in general, if the input space is real-valued, it makes more sense to use a continuous GA.

GA可以分为Binary和Continuous ，具体取决于我们要优化的问题类型。 可能所有问题都可以通过用二进制字符串表示其变量( 基因)来分解，但是总的来说，如果输入空间是实值，则使用连续 GA更有意义。

As there are fewer examples for continuous GA out there, the examples shown here will be for that version of GA.

由于那里连续GA的示例较少，因此此处显示的示例适用于该版本的GA。

Initialization

初始化

The search starts with a random population of N individuals. Each of those individuals corresponds to a chromosome, which encodes a sequence of genes representing a particular solution to the problem we’re trying to optimize for. Depending on the problem at hand, the genes representing the solution could be bits (0’s and 1’s) or continuous (real valued). An example of a real-valued chromosome representing a solution to a given problem with 9 variables (genes) is shown below.

搜索从N个个体的随机种群开始。 这些个体中的每一个都对应一条染色体 ，该染色体编码表示代表我们要优化的问题的特定解决方案的一系列基因。 根据当前的问题，代表解决方案的基因可以是位(0和1)或连续(实值)。 下面显示了一个实值染色体的示例，该染色体代表具有9个变量( 基因 )的给定问题的解决方案。

Fitness

适合度

The fitness of each individual is what defines what we are optimizing for, so that, given a chromosome encoding a specific solution to a problem, its fitness will correspond to how well that particular individual fares as a solution to the problem. Therefore, the higher its fitness value, the more optimal that solution is.

每个人的健康状况 是什么定义了我们要优化的内容，因此，给定染色体编码的问题的特定解决方案，其适应性将对应于特定个体解决问题的能力。 因此，其适用性值越高，该解决方案越理想。

After all, individuals have their fitness score calculated, they are sorted, so that the fittest individuals can be selected for crossover.

毕竟，已经计算了个人的健身得分，并对他们进行了排序，以便可以选择最适合的个人进行交叉。

Selection

选拔

Selection is the process by which a certain proportion of individuals are selected for mating between each other and create new offsprings. Just like in real-life natural selection, individuals that are fitter have higher chances of surviving, and therefore, of passing on their genes to the next generation. Though versions with more individuals exist, usually the selection process matches two individuals, creating pairs of individuals. There are four main strategies:

选择是选择特定比例的个体以使其彼此交配并产生新后代的过程。 就像现实中的自然选择一样，更健康的个体有更高的生存机会，因此可以将其基因传给下一代。 尽管存在更多个人的版本，但通常选择过程会匹配两个个人，从而创建成对的个人。 有四种主要策略：

pairing: This is perhaps the most straightforward strategy, as it simply consists of pairing the top fittest chromosomes two-by-two (pairing odd rows with even ones).

配对 ：这可能是最直接的策略，因为它仅包括将最合适的染色体两两配对(将奇数行与偶数行配对)。

random: This strategy consists of randomly selecting individuals from the mating pool.

随机 ：此策略包括从交配池中随机选择个体。

roulette wheel: This strategy also follows a random principle, but fitter individuals have higher probabilities of being selected.

轮盘赌 ：这种策略也遵循随机原则，但是更健康的人被选中的可能性更高。

tournament: With this strategy, the algorithm first selects a few individuals as candidates (usually 3), and then selects the fittest individual. This option has the advantage that it does not require the individuals to be sorted by fitness first.

比赛 ：采用这种策略时，算法首先选择一些个人作为候选者(通常为3个人)，然后选择最适合的个人。 该选项的优点是它不需要先按适合度对个人进行分类。

A python implementation for the roulette wheel strategy is shown on the snippet below.

下面的代码段显示了轮盘策略的python实现。

Crossover

交叉

This is the step where new offsprings are generated, which will then replace the least fit individuals in the population. The idea behind crossing over individuals is that, by combining different genes, we might produce even fitter individuals, which will be better solutions to our problem. Or not, and in that case, those solutions won’t survive to the next generations.

这是生成新后代的步骤，然后将替换种群中最不适合的个体。 跨越个体​​背后的想法是，通过组合不同的基因，我们甚至可以生产出更健康的个体，这将是解决我们问题的更好方法。 不管是不是，在那种情况下，这些解决方案都无法延续到下一代。

In order to perform the actual crossover, each of the pairs coming from the selection step are combined to produce two new individuals each, which will both have genetic material from each of the parents. There are several different strategies for performing the crossover, so for brevity, we’ll only discuss one of them.

为了进行实际的杂交，将来自选择步骤的每对配对以产生两个新个体，每个个体都具有来自每个亲本的遗传物质。 执行交叉有几种不同的策略，为简便起见，我们仅讨论其中一种。

Supposing we have a problem defined by 9 variables, if we have 2 parents and we choose randomly the crossover gene as index 3, then each of the offsprings will be a combination of each parent, as shown in the diagram below.

假设我们有一个由9个变量定义的问题，如果我们有2个父母，并且我们随机选择交叉基因作为索引3，那么每个后代将是每个父母的组合，如下图所示。

The crossover gene of each offspring is calculated according to the rule given by:

每个后代的交叉基因根据以下规则计算：

Where β will be a random number between 0 and 1. The python code for the crossover is given below.

其中β是0到1之间的随机数。下面给出了交叉的python代码。

Mutation

突变

Mutation is the process by which we introduce new genetic material in the population, allowing the algorithm to search a larger space. If it were not for mutation, the existing genetic material diversity in a population would not increase, and, due to some individuals “dying” between generations, would actually be reduced, with individuals tending to become very similar quite fast.

突变是我们在种群中引入新遗传物质的过程，从而使算法可以搜索更大的空间。 如果不是为了突变，则种群中现有的遗传物质多样性将不会增加，而且由于某些个体在世代之间“垂死”，实际上会减少，而个体趋于变得非常相似。

In terms of the optimization problem, this means that without new genetic material the algorithm can converge to local optima before it explores an enough large size of the input space to make sure that we can reach the global optimum. Therefore, mutation plays a big role in maintaining diversity in the population and allowing it to evolve to fitter solutions to the problem.

就优化问题而言，这意味着在没有新的遗传材料的情况下，该算法可以先收敛到局部最优，然后再探索足够大的输入空间，以确保我们可以达到全局最优。 因此，突变在维持种群多样性并使其进化以适应问题的解决方案中起着重要作用。

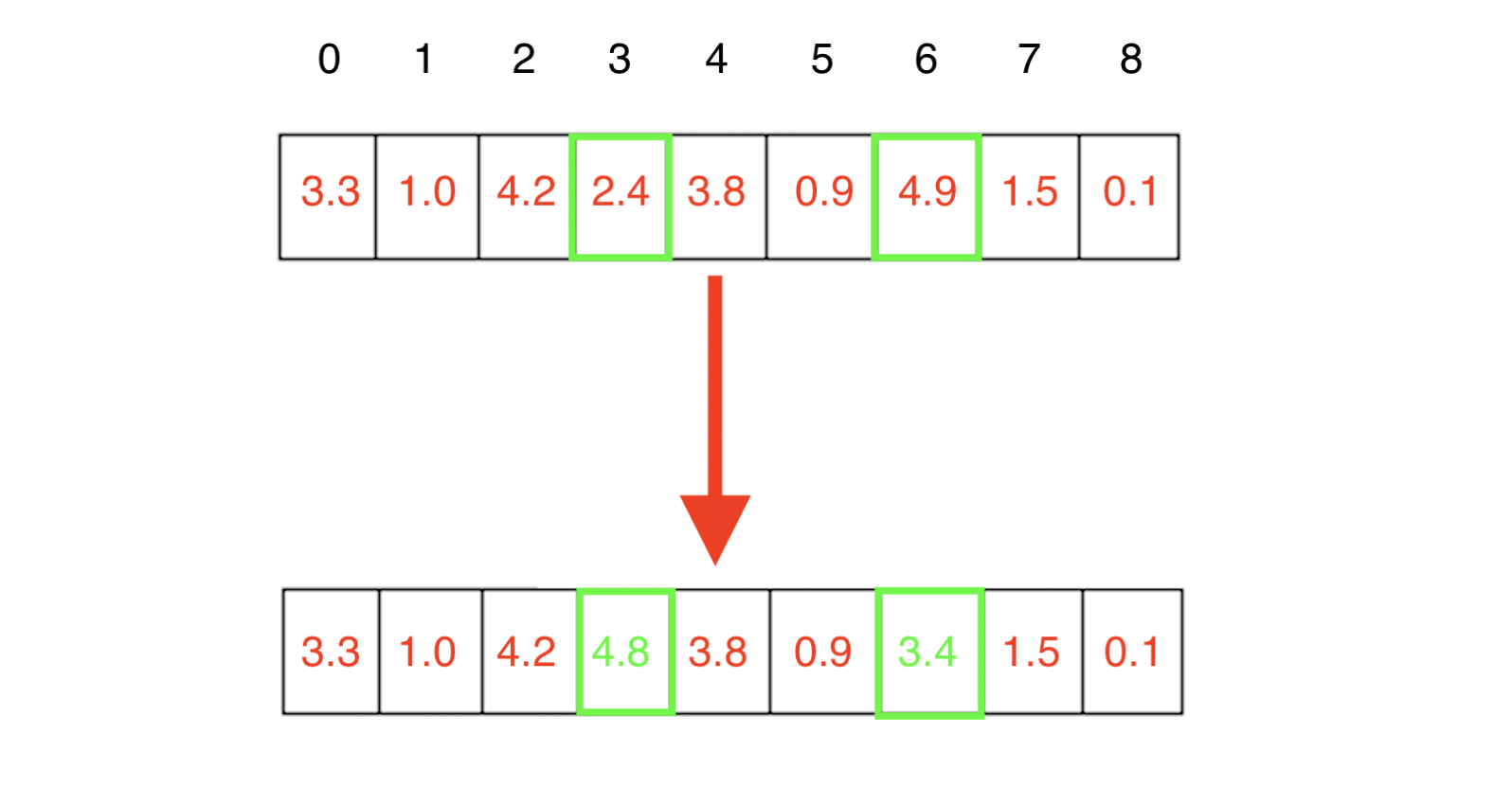
The most simple way we can do this is, given a certain mutation rate, to randomly choose some individuals and some genes and assign a new random number to those positions. This is exemplified in the diagram and code snippet below.

我们可以执行此操作的最简单方法是，在确定突变率的情况下 ，随机选择一些个体和某些基因，并为这些位置分配一个新的随机数。 下面的图和代码段中对此进行了举例说明。

Solver

解算器

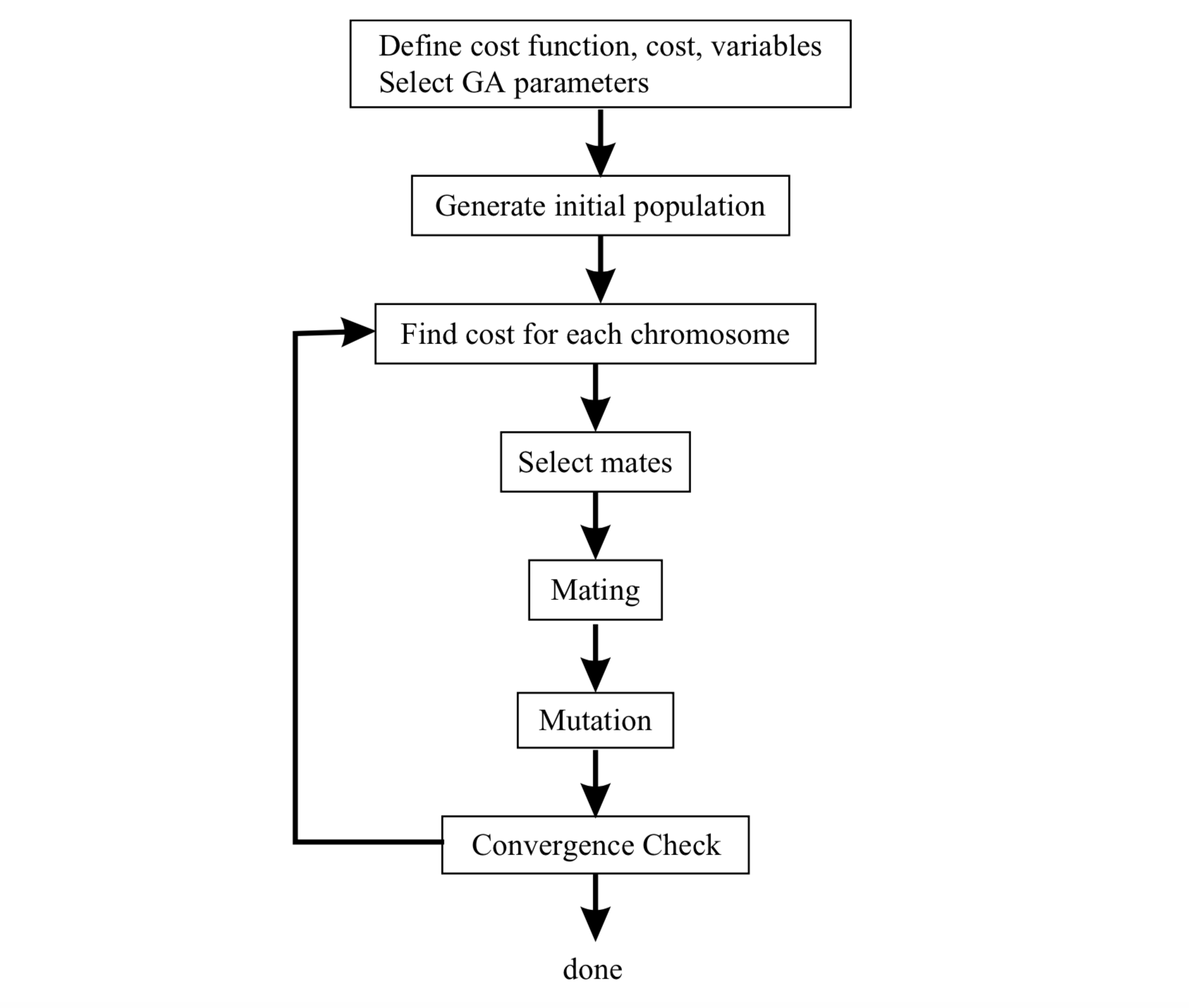
Now it’s time to tie it all together. Using the operators that we defined above, the algorithm can now solve the problem, with the actual main cycle of the algorithm being implemented in just a few lines of code. The flowchart of the algorithm, as well as an example implementation in python are shown below.

现在是时候将它们捆绑在一起了。 使用上面定义的运算符，该算法现在可以解决问题，该算法的实际主循环仅用几行代码即可实现。 该算法的流程图以及python中的示例实现如下所示。

介绍GeneAl (Introducing GeneAl)

GeneAl is a python library implementing Genetic Algorithms, which can be used and adapted to solve many optimization problems. One can use the provided out-of-the-box solver classes — BinaryGenAlgSolver and ContinuousGenAlgSolver — , or create a custom class which inherits from one of these, and implements methods that override the built-in ones. It also has support for solving the (in)famous Travelling Salesman Problem.

GeneAl是实现遗传算法的python库，可用于解决许多优化问题。 可以使用提供的现成的求解器类BinaryGenAlgSolver和ContinuousGenAlgSolver ，或者创建一个自定义类继承自其中的类，并实现覆盖内置方法的方法。 它还支持解决著名的旅行推销员问题 。

For brevity, we’ll only see how to use the continuous version — keeping in line with this post — , but for more details, check out the README of this project.

为简便起见，我们只会看到如何使用连续版本-与本文保持一致-，但是要了解更多详细信息，请查看该项目的自述文件。

The first thing would be to install the package, which can be made through pip, as such:

首先是要安装软件包，可以通过pip进行安装，如下所示：

pip install geneal 

After the installation completes, one is ready to use it. So let’s see how we can use the ContinuousGenAlgSolver class.

安装完成后，就可以使用了。 因此，让我们看看如何使用ContinuousGenAlgSolver类。

As a bare minimum, the class requires the user to provide the number of genes present in the problem, as well as to provide the custom defined fitness function. For convenience, the library provides some default fitness functions that can be used for testing.

至少，该类别要求用户提供问题中存在的基因数量，并提供自定义的适应度函数。 为了方便起见，该库提供了一些可用于测试的默认适应性函数。

With the initialization done above, the class will solve the problem using default values for all the parameters. If we wish to have more control over the algorithm run, we will want to adjust these, and that can be done as shown below:

通过上面的初始化，该类将使用所有参数的默认值解决问题。 如果我们希望对算法的运行有更多的控制，我们将希望对其进行调整，如下所示：

Finally, this class allows the user to specify the type of problem — if the possible values are integers or floats — , as well as the variables’ limits, in order to limit the search space.

最后，该类允许用户指定问题的类型(如果可能的值是整数或浮点数)以及变量的限制，以限制搜索空间。

This completes this short introduction to the library. If you want to know more, check out the GitHub repository, which has more information 🙂

这样就完成了对库的简短介绍。 如果您想了解更多信息，请查看GitHub存储库 ，其中包含更多信息:)

Thanks for reading!

谢谢阅读！