机器学习笔记——14 矩阵谱分解与奇异值分解及其背后的线性算子理论 (实战项目：利用SVD进行图像压缩)

机器学习笔记——14 矩阵谱分解与奇异值分解及其背后的线性算子理论 (实战项目：利用SVD进行图像压缩)

本篇文章介绍矩阵的谱分解与奇异值分解 (Singular Values Decomposition,SVD)，为了对其有一个更为本质性地认识，本文从线性算子的理论讲起，我们介绍算子的实谱定理和奇异值分解定理，然后在此基础上，借用线性算子的理论对矩阵的两个分解进行解释。
对矩阵分解的理论进行讨论后，我们将着眼于具体的操作，对于一个矩阵，如何找到其分解形式。最后我们利用讨论完的结果，利用SVD实现对一幅图像的压缩，实际上图像可以视为一个矩阵，因此可以通过找到该矩阵的分解形式，保留主要成分实现压缩。

线性算子理论与对称矩阵的谱分解

线性算子即是我们常说的线性变换，关于线性变换的定义与理论，可详见线性代数，本文只介绍与SVD有关的部分。
首先我们关注地更多是内积空间中的算子 (operator)，在众多的算子，有一些算子性质优良，那么什么样的算子性质比较好？
首先为了处理的方便，我们常常会选择一组规范正交基，如此一来，我们通过一组选定的基，就可以建立相应维度的矩阵与线性算子的同构，而所谓的性质良好的算子

ϕ

\phi

ϕ，指的即是：
在内积空间中存在一组规范正交基u，使得该算子

ϕ

\phi

ϕ对应到一个对角矩阵

Σ

\Sigma

Σ，即

ϕ

(

u

x

u

)

=

u

Σ

x

u

\phi(ux_u) = u \Sigma x_u

ϕ(uxu​)=uΣxu​。
由此我们引出线性代数中一个很好的定理：
实谱定理：在实数域R中，具有上述性质的算子的充要条件为：

<

ϕ

(

v

)

,

w

>

=

<

v

,

ϕ

(

w

)

>

<\phi(v),w> = <v,\phi(w)>

<ϕ(v),w>=<v,ϕ(w)>，满足该条件的算子称为自伴算子。
注：本文所述定理的证明，可以参考《liner Algebra done right》
至此为止，我们就可以从算子理论的角度来解释为何实对称矩阵一定可以对角化。 若A是对称矩阵，则我们在内积空间中随意选择规范正交基

v

v

v，则A唯一对应到一个线性算子，记之为

ϕ

\phi

ϕ。可以证明算子

ϕ

\phi

ϕ是自伴算子，由此根据算子的实谱定理，我们能够找到由该算子的特征向量构成的规范正交基，记之为

v

v

v，使得自伴算子

ϕ

\phi

ϕ在该基

u

u

u下，其对应矩阵是对角阵，记之为

Σ

\Sigma

Σ。从而对于一个内积空间中的元素

x

x

x,记其在基

u

u

u下的坐标为

x

u

x_u

xu​，在基

v

v

v下的坐标为

x

v

x_v

xv​，从而有x的两个表示：

u

x

u

=

v

x

v

u x_u = v x_v

uxu​=vxv​即从基

u

u

u到基

v

v

v的转换矩阵为

U

U

U，易知

U

U

U是一个正交矩阵，从而有

u

=

v

U

u = v U

u=vU

x

v

=

U

x

u

x_v = Ux_u

xv​=Uxu​利用此二式，代入下式

v

A

x

v

=

u

Σ

x

u

v A x_v = u \Sigma x_u

vAxv​=uΣxu​则有

A

U

=

U

Σ

AU = U\Sigma

AU=UΣ利用正交矩阵的性质，即有

A

=

U

Σ

U

T

A = U\Sigma U^T

A=UΣUT此即实对称矩阵的谱分解：

A

=

∑

i

=

1

n

λ

i

u

i

u

i

T

A = \sum_{i = 1}^{n}\lambda_i u_iu_i^T

A=i=1∑n​λi​ui​uiT​
以上是对谱分解的理论分析，我们从借助算子理论来分析，从而可以看到更为本质的原因，即对称阵在规范正交基下对应于自伴算子。

实际操作中，我们可以选择基

v

v

v为标准正交基。从而对于对称阵A，我们找出他的所有特征值，形成对角阵

Σ

\Sigma

Σ，然后找出相应的特征向量，将其规范正交化，形成正交阵U，从而完成谱分解。

线性算子理论与一般矩阵的奇异值分解

上部分的实谱定理表明，只有自伴算子可以达到我们的目的， 从几何直观上看，相当于找到一个直角坐标系，使得该算子在该坐标系上的表现为各分量的伸缩变换。 当时，对于更多的不是自伴算子的算子而言，如何能够找到好的算子理论，使得对该算子有更好的理解呢。我们陈述算子的奇异值分解定理：
对于任何一个算子

ϕ

\phi

ϕ，都能找到两组规范正交基，记之为

v

v

v和

u

u

u，并能够对应到一个对角阵

Σ

\Sigma

Σ，从而使得

ϕ

(

v

x

v

)

=

u

Σ

x

v

\phi(vx_v) = u\Sigma x_v

ϕ(vxv​)=uΣxv​。
注意到与之前实谱定理中要求的不一样，我们这里允许使用两组规范正交基，几何上讲，允许使用两个直角坐标系。其中对角阵

Σ

\Sigma

Σ的对角元素为算子

ϕ

\phi

ϕ的奇异值，即自伴算子

ϕ

∗

ϕ

\sqrt{\phi^*\phi}

ϕ∗ϕ
​的特征值。
至此，我们就可以来解释为何任何一个矩阵均可以做奇异值分解。对于矩阵A，在内积空间中，先随意选择一组规范正交基，记之为

e

e

e，则A矩阵对应到一个线性算子，记之为

ϕ

\phi

ϕ。根据算子的奇异值分解，我们可以找到两组规范正交基，记之为

u

u

u和

v

v

v。内积空间中的元素

x

x

x，在三个坐标系下的坐标分别记为

x

e

x_e

xe​、

x

u

x_u

xu​、

x

v

x_v

xv​。则有基转换矩阵

U

U

U和

V

V

V(军事正交矩阵)，使得

u

=

e

U

u = e U

u=eU

v

=

e

V

v = e V

v=eV
对于坐标，有

x

e

=

V

x

v

x_e = V x_v

xe​=Vxv​

x

e

=

U

x

u

x_e = U x_u

xe​=Uxu​
利用算子的奇异值分解定理，有

ϕ

(

x

)

=

ϕ

(

v

x

v

)

=

u

Σ

x

v

=

e

U

Σ

x

v

\phi(x) = \phi(v x_v) = u \Sigma x_v = e U \Sigma x_v

ϕ(x)=ϕ(vxv​)=uΣxv​=eUΣxv​
而根据矩阵A，有

ϕ

(

x

)

=

ϕ

(

e

x

e

)

=

e

A

x

e

=

e

A

V

x

v

\phi(x) = \phi(e x_e) = e A x_e = e A V x_v

ϕ(x)=ϕ(exe​)=eAxe​=eAVxv​
从而有

U

Σ

=

A

V

U \Sigma = A V

UΣ=AV此即

A

=

U

Σ

V

T

A = U \Sigma V^T

A=UΣVT
注意，以上从理论上证明了任何矩阵奇异值分解的存在性，实际操作中，根据算子理论，则

Σ

\Sigma

Σ的对角元素

λ

\lambda

λ是矩阵

A

T

A

\sqrt{A^TA}

ATA
​的特征值，我们可以计算

A

T

A

A^TA

ATA的特征值，然后进行开平方即可。对于

U

U

U与

V

V

V的找，有

A

T

A

=

V

Σ

2

V

T

A^TA = V \Sigma^2V^T

ATA=VΣ2VT

A

A

T

=

U

Σ

2

U

T

AA^T = U \Sigma^2U^T

AAT=UΣ2UT从而U与V分别是对称矩阵

A

A

T

AA^T

AAT和

A

T

A

A^TA

ATA的特征向量规范正交化后的矩阵。至此得到一般矩阵A的奇异值分解过程。

利用SVD进行图像压缩（python实现）

一些说明与注意事项：

• 压缩比例分析：假设图像原来的像素点为mn，则总共需要存储mn个数据。现在通过SVD，假设我们保留了前k个奇异值，此时只需要保留km + k*n + k = k(m+n+1)个数据，比例为$$rate=\frac{k(m+n+1)}{mn}\approx k(\frac{1}{m}+\frac{1}{n})$$本例中的像素点为512 * 512，如果保留16个主要奇异值的话，其压缩比例rate = 6.25%，保留64个奇异值的话，压缩比为rate = 25%。
• 奇异值的意义：SVD相当于把矩阵分解为各个秩一小矩阵的和，其中奇异值代表着这个矩阵的重要程度，通过归一化可以更直观地看到这一点。于是我们保留的顺序应当是从大到小。除了压缩图像之外，SVD还要很多用途，比如图像去噪，通过去除一些较小的奇异值，可以有效去除一些干扰因素。
• SVD压缩图像的与kmean压缩图像的比较：SVD在恢复出图像时，需要比较大量的计算，而kmean不需要，但SVD压缩图像是稳定的，过程也不需要迭代。此外，SVD的压缩效果同kmean是很不同的，其是模糊铺开的，随着成分的加入更加清晰，而kmean是通过颜色聚块的，因此根据需求选择不同的压缩方法。
• 压缩结果展示：
  保留成分数：1，rate = 0.39%
  
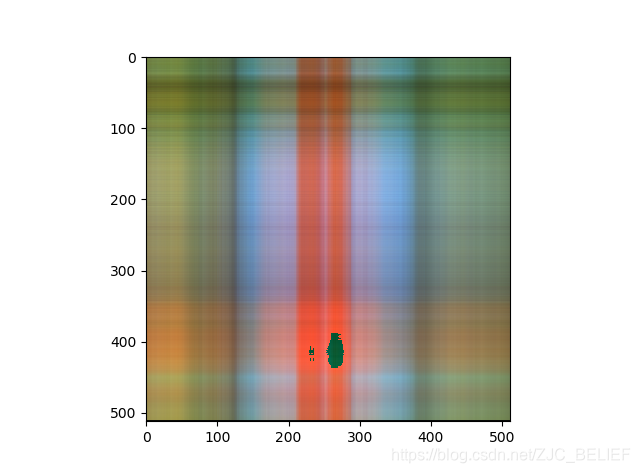
  保留成分数：8，rate = 3.125%
  
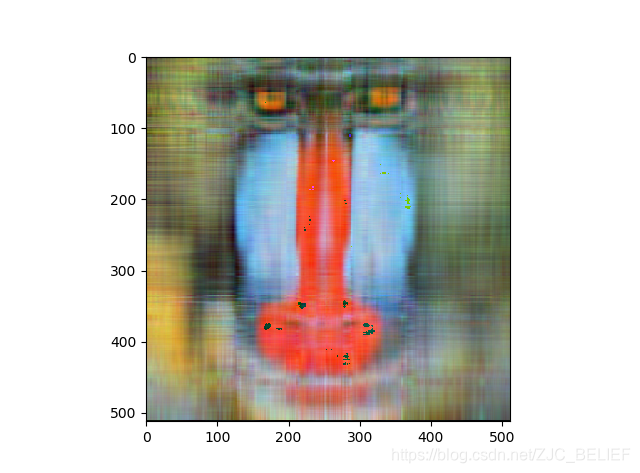
  保留成分数：16，rate = 6.25%
  
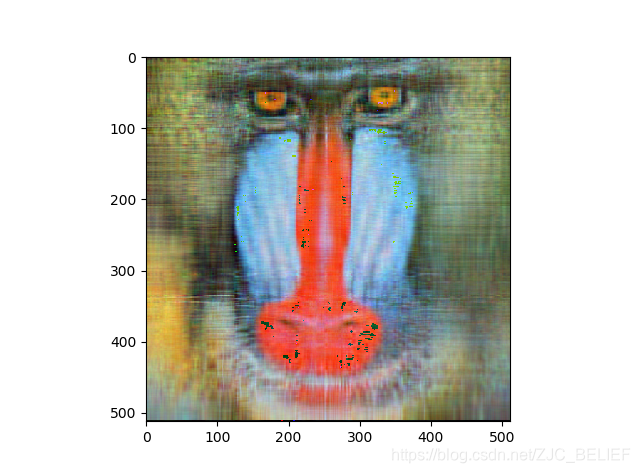
  保留成分数：32，rate = 12.5%
  
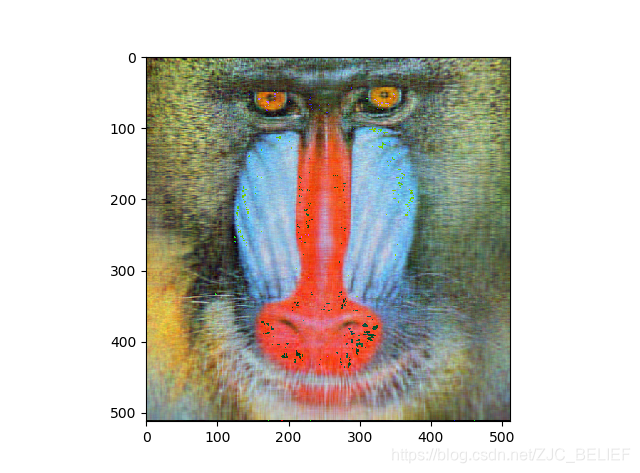
  保留成分数：64，rate = 25%
  

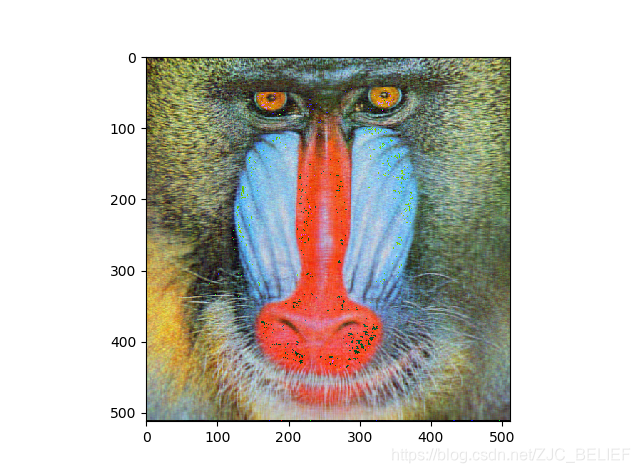
from matplotlib.image import imread
import matplotlib.pyplot as plt
import numpy as np

def main():
    # 读取图片的矩阵数据
    Image = imread('C:/Users/Administrator/Desktop/MLCourseOfWSQ/pythonProject/mlData/svd/mandrill-large.tiff')
    Image = Image.astype(np.float64)

    # 图像的层数
    repeat = Image.shape[2]
    # 保留的成分数
    saveK = 100
    # 建立压缩后的图像数组
    ImageCompress = np.zeros(Image.shape,dtype = np.uint8)
    for i in range(repeat):
        ImageCompress[:,:,i] = svd(Image[:,:,i],saveK)
    
    plt.imshow(ImageCompress)
    plt.show()
    
def svd(Image,saveK):
    '''
    本函数利用矩阵SVD，按照saveK保留成分数
    '''
    U,singularValue,V = np.linalg.svd(Image)
    # 利用奇异值建立对角阵
    S = np.diag(singularValue)
    ImageCompress = U[:,:saveK].dot(S[:saveK,:saveK]).dot(V[:saveK,:])
    return ImageCompress
    
if __name__ == '__main__':
    main()