相比于点特征,直线段特征对视角和光照变化具有很好的鲁棒性。常用的直线检测有Hough直线检测和LSD等.Hough直线检测将直线检测映射为参数空间中点的检测,而LSD通过查找近似矩形区域来获得直线。相比于Hough直线检测,LSD算法具有结果准确,误检可控,同时不需要调节参数的优点。这里主要介绍LSD算法。
下面是LSD算法流程:
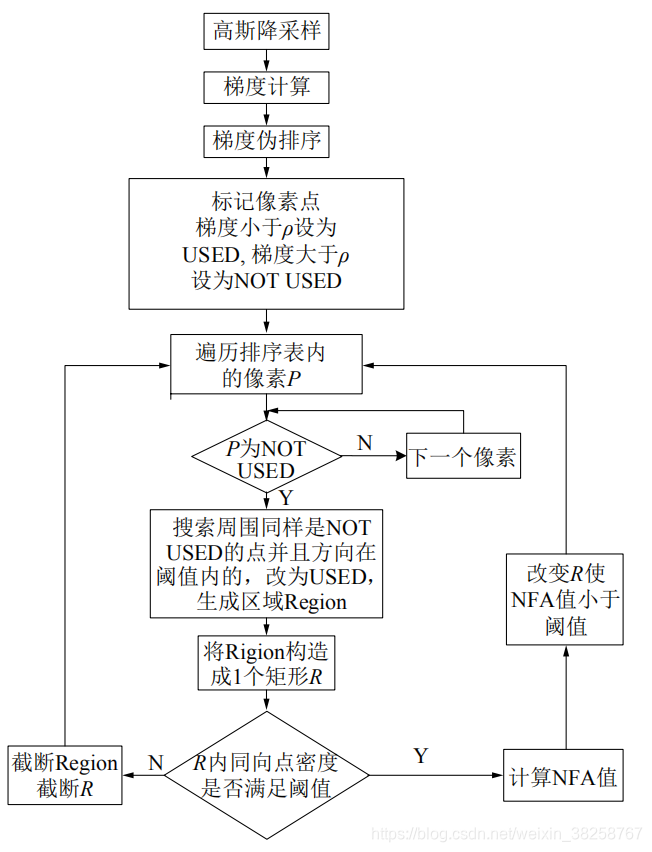
- 高斯降采样即高斯模糊后降采样,这里是为了减弱锯齿效应
- 梯度计算
这里梯度的大小定义为:
G
(
x
,
y
)
=
g
x
2
(
x
,
y
)
+
g
y
2
(
x
,
y
)
G(x,y)=\sqrt{g_x^2(x,y)+g_y^2(x,y)}
G(x,y)=gx2(x,y)+gy2(x,y)
水平角(LLA)定义为:
arctan
(
g
x
(
x
,
y
)
−
g
y
(
x
,
y
)
)
\arctan(\frac{g_x(x,y)}{-g_y(x,y)})
arctan(−gy(x,y)gx(x,y)) - 伪排序是指将梯度分为1024个桶,将梯度放入相应桶中,并不做全排序。这里认为梯度越大,越可能是直线。
- 区域生长

这里的角度阈值τ
\tau
τ是一个经验值π
8
\frac{\pi}{8}
8π - 构造矩形
矩形的中心点由下面的公式确定:
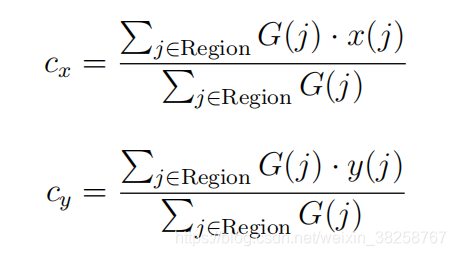
矩形的主方向为矩阵M
M
M最小特征值对应的特征向量确定:
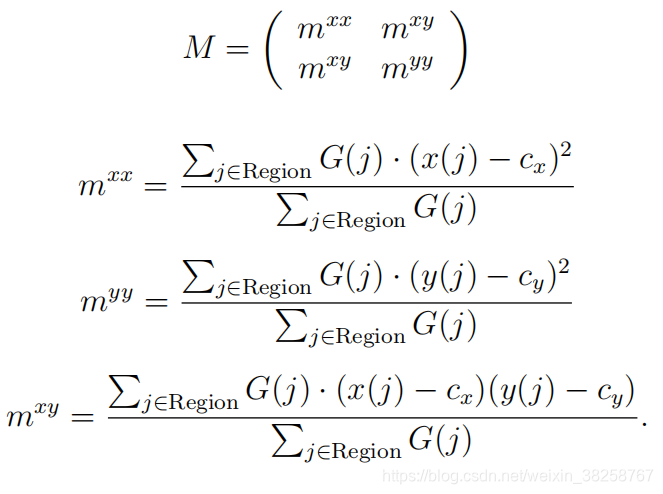
矩形的长宽由最小包围盒确定。 - 同向点密度检测
这里是为了解决下图的情况
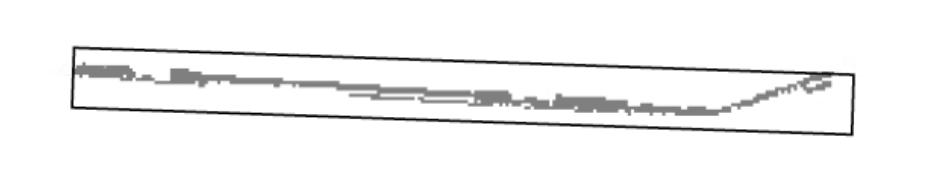
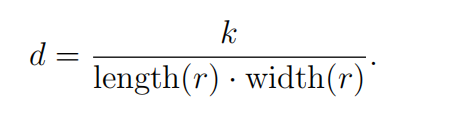
对于d
d
d值小于阈值的情况,可以有两种解决方式:
1、减小角度容忍阈值
2、缩小区域半径 - 矩形的修正
这里需要计算NFA值,个人理解为:它可以看作伯努利分布下,随机获得的矩形内梯度一致性要好于当前矩形内梯度一致性的情况数,该数值越小,则当前矩形内梯度的一致性越好。
NFA的定义为:
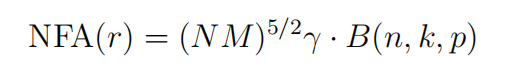
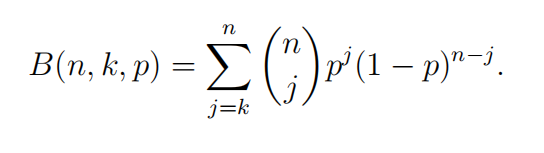
这里p
p
p的初始值为τ
π
\frac{\tau}{\pi}
πτ,γ
\gamma
γ为所有尝试过的p
p
p值数,根据下面的修正方法,该值应为11
11
11.
当NFA大于阈值使,按下面步骤调整获得最终的矩形:
1.减小p=p/2
2.短边减少一行
3.长边减少一行
4.长边减少另一行
5.减小p=p/2
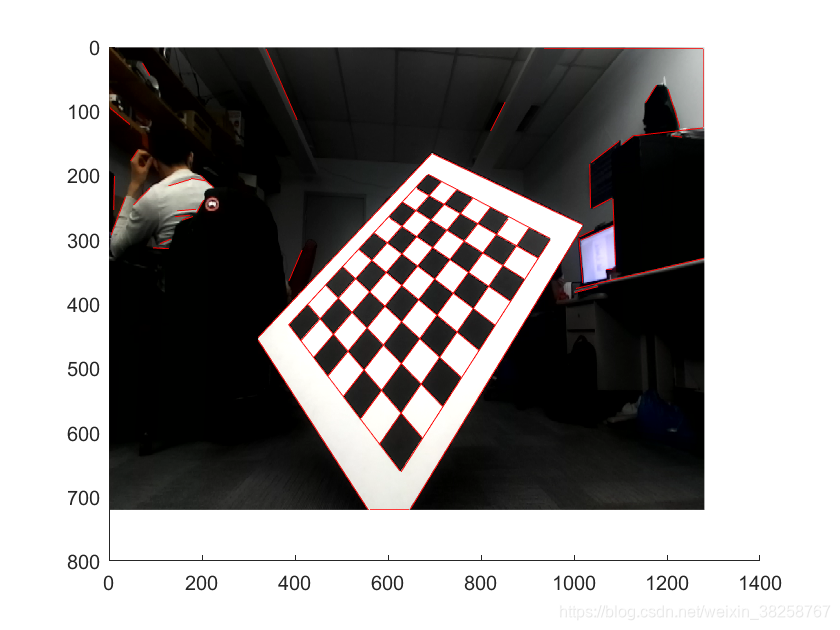
矩形中线即为检测到的直线。
matlab实现:https://github.com/Garyandtang/Gary_LSD
参考:
https://www.ipol.im/pub/art/2012/gjmr-lsd/article.pdf
http://kns.cnki.net/kcms/detail/23.1191.U.20181220.1128.006.html
https://www.cnblogs.com/Jessica-jie/p/7512152.html