1.前言
下文中描述坐标系使用了英文的简写
OS:Origin Space 原始空间坐标系
NS:New Space 新空间坐标系
2.坐标变换介绍
为了解决这个问题,可以利用机器人学中的位姿变换来进行描述,以下依次介绍坐标平移、坐标旋转和刚体的一般变换,再介绍齐次矩阵的使用(如果有了基础可以直接跳过这一部分),最后回过头来解决上面的问题。
2.1 坐标平移

描述:坐标系NS和坐标系OS有相同的方位,但是NS的坐标原点和OS的不重合。
由矢量的平行四边形法则,一点
A
A
A在两个坐标系NS和OS中的描述
N
S
p
A
^{NS}\mathbf{p}_{A}
NSpA和
O
S
p
A
^{OS}\mathbf{p}_{A}
OSpA满足以下的关系:
N
S
p
A
=
O
S
p
A
+
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{A} =^{OS}\mathbf{p}_{A} +^{NS}\mathbf{p}_{OS-O}
NSpA=OSpA+NSpOS−O
式中:
N
S
p
A
^{NS}\mathbf{p}_{A}
NSpA:
A
A
A在坐标系
NS中的坐标
O
S
p
A
^{OS}\mathbf{p}_{A}
OSpA:
A
A
A在坐标系
OS中的坐标
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{OS-O}
NSpOS−O:坐标系
OS原点在坐标系NS中的坐标
2.2 坐标旋转

描述:坐标系NS和坐标系OS有相同的坐标原点,两者的姿态不同,用旋转矩阵
O
S
N
S
R
_{OS}^{NS}\mathbf{R}
OSNSR来描述坐标系OS相对于NS的姿态,同一点
A
A
A在两个坐标系NS和OS中的描述
N
S
p
A
^{NS}\mathbf{p}_{A}
NSpA和
O
S
p
A
^{OS}\mathbf{p}_{A}
OSpA满足以下的关系:
N
S
p
A
=
O
S
N
S
R
O
S
p
A
^{NS}\mathbf{p}_{A}=_{OS}^{NS}\mathbf{R}^{OS}\mathbf{p}_{A}
NSpA=OSNSROSpA
式中:
N
S
p
A
^{NS}\mathbf{p}_{A}
NSpA:
A
A
A在坐标系
NS中的坐标
O
S
p
A
^{OS}\mathbf{p}_{A}
OSpA:
A
A
A在坐标系
OS中的坐标
KaTeX parse error: Got group of unknown type: ‘internal’,描述坐标系OS相对于NS的方位
【其中N
S
x
O
S
^{NS}\mathbf{x_{OS}}
NSxOS
N
S
y
O
S
^{NS}\mathbf{y_{OS}}
NSyOS
N
S
z
O
S
^{NS}\mathbf{z_{OS}}
NSzOS分别是坐标系
OS三个坐标轴对应的单位矢量(
1
,
0
,
0
)
T
(1,0,0)^T
(1,0,0)T、
(
0
,
1
,
0
)
T
(0,1,0)^T
(0,1,0)T、
(
0
,
0
,
1
)
T
(0,0,1)^T
(0,0,1)T在坐标系
NS中的坐标表示】
旋转矩阵的性质(这里不介绍具体的推导,机器人学的书有讲的)只讲结论:
①
N
S
O
S
R
=
O
S
N
S
R
−
1
=
O
S
N
S
R
T
②
d
e
t
(
N
S
O
S
R
)
=
1
\begin{aligned} &①_{NS}^{OS}\mathbf{R}=_{OS}^{NS}\mathbf{R}^{-1}=_{OS}^{NS}\mathbf{R}^T\\&②det(_{NS}^{OS}\mathbf{R})=1 \end{aligned}
①NSOSR=OSNSR−1=OSNSRT②det(NSOSR)=1
2.3 刚体的一般变换

描述:坐标系NS和坐标系OS坐标原点不同,两者的姿态也不同,一点
A
A
A在两个坐标系NS和OS中的描述
N
S
p
A
^{NS}\mathbf{p}_{A}
NSpA和
O
S
p
A
^{OS}\mathbf{p}_{A}
OSpA满足以下的关系:
N
S
p
A
=
O
S
N
S
R
O
S
p
A
+
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{A} =_{OS}^{NS}\mathbf{R}^{OS}\mathbf{p}_{A} +^{NS}\mathbf{p}_{OS-O}
NSpA=OSNSROSpA+NSpOS−O
式中:
N
S
p
A
^{NS}\mathbf{p}_{A}
NSpA:
A
A
A在坐标系
NS中的坐标
O
S
p
A
^{OS}\mathbf{p}_{A}
OSpA:
A
A
A在坐标系
OS中的坐标
KaTeX parse error: Got group of unknown type: ‘internal’,描述坐标系OS相对于NS的方位
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{OS-O}
NSpOS−O:坐标系
OS原点在坐标系NS中的坐标
推导实际上是引入一个中间过渡坐标系NS',把一般变换看作是坐标旋转和坐标平移的共同结果,推导略去,读者感兴趣可以自行推导一下,也可以看看机器人学的相关书籍。
2.4 齐次变换
为了统一坐标平移和旋转变换,定义齐次变换矩阵:
T
=
[
O
S
N
S
R
N
S
p
O
S
−
O
0
1
]
\mathbf{T}=\begin{bmatrix}_{OS}^{NS}\mathbf{R}&^{NS}\mathbf{p}_{OS-O}\\ 0&1\end{bmatrix}
T=[OSNSR0NSpOS−O1]
这样,3.3中的复合变换可以写成
[
N
S
p
A
1
]
=
[
O
S
N
S
R
N
S
p
O
S
−
O
0
1
]
[
O
S
p
A
1
]
=
T
[
O
S
p
A
1
]
\begin{bmatrix}^{NS}\mathbf{p}_{A}\\1\end{bmatrix}=\begin{bmatrix}_{OS}^{NS}\mathbf{R}&^{NS}\mathbf{p}_{OS-O}\\ 0&1\end{bmatrix}\begin{bmatrix}^{OS}\mathbf{p}_{A}\\1\end{bmatrix}=\mathbf{T}\begin{bmatrix}^{OS}\mathbf{p}_{A}\\1\end{bmatrix}
[NSpA1]=[OSNSR0NSpOS−O1][OSpA1]=T[OSpA1]
我们的目标就是求取旋转矩阵
O
S
N
S
R
_{OS}^{NS}\mathbf{R}
OSNSR和平移矢量
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{OS-O}
NSpOS−O。
现在我们已经搞清楚坐标系变换的概念了,那么下面这个问题你能试着解决吗?先不看具体怎么解,自己做做看?
3.问题描述
如图,给定坐标系NS的三个坐标轴单位向量在坐标系OS中的坐标(两两正交),以及NS的原点在坐标系OS中的坐标,现已知坐标系OS中点A的坐标,求在坐标系NS中的点A的坐标表示。

4.问题分析
由题目分析,我们知道的条件有:
坐标系NS的三个坐标轴单位向量在坐标系OS中的坐标(两两正交)——
N
S
O
S
R
_{NS}^{OS}\mathbf{R}
NSOSR
NS的原点在坐标系OS中的坐标——
O
S
p
N
S
−
O
^{OS}\mathbf{p}_{NS-O}
OSpNS−O
坐标系OS中点A的坐标——
O
S
p
A
^{OS}\mathbf{p}_{A}
OSpA
列出3.4中的公式:
[
N
S
p
A
1
]
=
[
O
S
N
S
R
N
S
p
O
S
−
O
0
1
]
[
O
S
p
A
1
]
\begin{bmatrix}^{NS}\mathbf{p}_{A}\\1\end{bmatrix}=\begin{bmatrix}_{OS}^{NS}\mathbf{R}&^{NS}\mathbf{p}_{OS-O}\\ 0&1\end{bmatrix}\begin{bmatrix}^{OS}\mathbf{p}_{A}\\1\end{bmatrix}
[NSpA1]=[OSNSR0NSpOS−O1][OSpA1]
我们需要求的是
O
S
N
S
R
_{OS}^{NS}\mathbf{R}
OSNSR,
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{OS-O}
NSpOS−O
①求
O
S
N
S
R
_{OS}^{NS}\mathbf{R}
OSNSR
这个问题很简单,由旋转矩阵的定义,可以知道,转置一下即可
O
S
N
S
R
=
N
S
O
S
R
T
_{OS}^{NS}\mathbf{R}=_{NS}^{OS}\mathbf{R}^T
OSNSR=NSOSRT
②求
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{OS-O}
NSpOS−O
写出表达式
N
S
p
A
=
O
S
N
S
R
O
S
p
A
+
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{A} =_{OS}^{NS}\mathbf{R}^{OS}\mathbf{p}_{A} +^{NS}\mathbf{p}_{OS-O}
NSpA=OSNSROSpA+NSpOS−O
令
A
A
A为坐标系NS的原点,
N
S
p
N
S
−
O
=
O
S
N
S
R
O
S
p
N
S
−
O
+
N
S
p
O
S
−
O
^{NS}\mathbf{p}_{NS-O} =_{OS}^{NS}\mathbf{R}^{OS}\mathbf{p}_{NS-O} +^{NS}\mathbf{p}_{OS-O}
NSpNS−O=OSNSROSpNS−O+NSpOS−O
左边
N
S
p
N
S
−
O
^{NS}\mathbf{p}_{NS-O}
NSpNS−O很显然坐标系原点在坐标系NS中为零向量。故而
⇒
0
=
O
S
N
S
R
O
S
p
N
S
−
O
+
N
S
p
O
S
−
O
⇒
N
S
p
O
S
−
O
=
−
O
S
N
S
R
O
S
p
N
S
−
O
⇒
N
S
p
O
S
−
O
=
−
N
S
O
S
R
T
⋅
O
S
p
N
S
−
O
\begin{aligned}&\Rightarrow \mathbf{0} =_{OS}^{NS}\mathbf{R}^{OS}\mathbf{p}_{NS-O} +^{NS}\mathbf{p}_{OS-O} \\& \Rightarrow ^{NS}\mathbf{p}_{OS-O}=-_{OS}^{NS}\mathbf{R}^{OS}\mathbf{p}_{NS-O}\\&\Rightarrow ^{NS}\mathbf{p}_{OS-O}=-_{NS}^{OS}\mathbf{R}^T \cdot^{OS}\mathbf{p}_{NS-O}\end{aligned}
⇒0=OSNSROSpNS−O+NSpOS−O⇒NSpOS−O=−OSNSROSpNS−O⇒NSpOS−O=−NSOSRT⋅OSpNS−O
综上:
T
=
[
N
S
O
S
R
T
−
N
S
O
S
R
T
⋅
O
S
p
N
S
−
O
0
1
]
\mathbf{T}=\begin{bmatrix}_{NS}^{OS}\mathbf{R}^T&-_{NS}^{OS}\mathbf{R}^T \cdot^{OS}\mathbf{p}_{NS-O}\\ 0&1\end{bmatrix}
T=[NSOSRT0−NSOSRT⋅OSpNS−O1]
4.问题求解
%% 给定坐标系NS的三个坐标轴单位向量在坐标系OS中的坐标,都是归一化矢量且两两正交x0 y0 z0 ... x3 y3 z3 x y z都可以进行修改
p_NSo_in_OS=[x0 y0 z0];
XVector_NS_in_OS=[x1 y1 z1];
YVector_NS_in_OS=[x2 y2 z2];
ZVector_NS_in_OS=[x3 y3 z3];
R_NS_in_OS=[XVector_NS_in_OS',YVector_NS_in_OS',ZVector_NS_in_OS'];
p_OSo_in_NS=-R_NS_in_OS'*p_NSo_in_OS';
p_A_in_OS=[x y z];
T=[R_NS_in_OS',p_OSo_in_NS;0,0,0,1];
p_A_in_NS=T*[p_A_in_OS';1];
p_A_in_NS=p_A_in_NS(1:3,:);
p_A_in_NS=round(p_A_in_NS',4);%保留四位小数
测试了一系列点:
原坐标系中的坐标
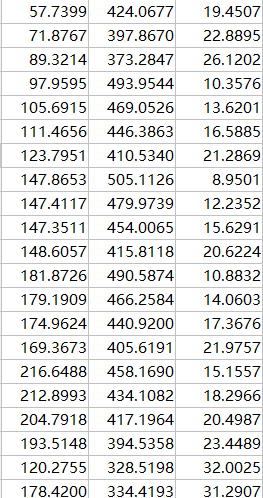
利用上面的原理写出齐次矩阵
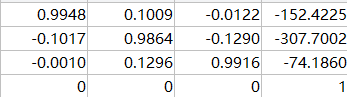
转换到新坐标系中的坐标
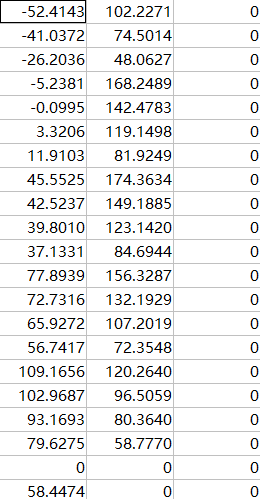
可以看到z坐标的维度都变成一样的了。是可以进行实现的。