之前总是会有个错觉，总觉得分库分表是很好的方案，其实前提是要在业务中的慢查询的SQL语句用尽了一切的优化方法之后，查询效率还是达不到我们的要求，这个时候再考虑分库分表。因为在对数据库中的数据进行拆分的时候，也会带来以下问题：

• 事务问题；
• 跨表分页、排序、函数问题；
• 全局主键避重问题；
• 数据迁移、扩容问题。

事务问题

目前数据库能够实现本地事务，也就是在同一个数据库中，可以允许一组操作要么全都正确执行，要么都不执行，从而确保数据库的一致性。单从分区角度出发，实际上仍然是一张表，一个库中，它不会存在事务一致性的问题，但是会使得事务变得非常复杂。

而单库分表和分库分表会涉及到分布式事务，目前数据库并不支持跨库事务，所以在这一块需要解决分布式事务可能带来的不一致性。

分页、排序、函数问题

分页需要按照执行的字段进行排序，当排序字段就是分片字段的时候，通过分片规则就比较容易定位到指定的分片；当排序字段并非分片字段的时候，就需要在不同分区、分表中进行排序并且返回，然后再将不同分区、分表中返回的结果集进行汇总和再次排序，最终得到返回结果。

取得页数越多，性能受影响也就越大。因为在分区、分表的时候都已经限定了分片字段，而其他字段是跟着分片的字段被分到不同的区域或者表中，这样各个分区、分表中的数据可能是随机的，为了排序的准确定，需要将所有分区、分表节点的前N也数据都排好序做合并，最后进行整体排序，这样的操作是非常耗费CPU和内存资源的，所以在分区、分表的情况下、分页数越大，系统的性能也会越差。

同样、在使用聚合函数，如Max、Min、Sum、Count进行计算的时候，也会像排序那样在每个分区、分表是哪个执行相应的函数，然后再将各个分区、分表的结果集进行汇总和再次计算，最终将结果返回。

全局主键避重问题

该问题主要针对分库分表环境中，由于表中的数据同时存在不同的数据库中，某个分区数据库生成的ID无法保证全局唯一，因为需要单独设计全局主键，用来避免跨库主键重复问题。一些常见的主键生成策略：

1、UUID：32个16进制数字，全球唯一，本地生成，性能高，没有网络耗时，但是非常长，占用大量的存储空间，并且作为主键建立索引和基于索引查询的时候会存在性能问题，一般这种方式不采用。

2、设置步长：设置主键ID增长的步长就是数据库的数量，起始值一开始就错开，能将ID的生成散列到各个数据库上。但是也有明显的缺点，如果还需要增加分库的时候，ID增长的步长需要改变，所以水平扩展比较复杂。

3、Snowflake（雪花算法）：分布式自增ID算法，64位Long型数字，组成部分：

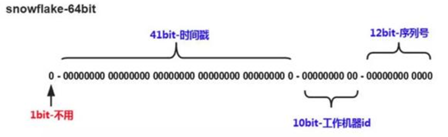
•  第一位未使用；
• 接下来是41位毫秒级时间，41位的长度可以表示69年的时间；
• 5位datacenterId，5位workerId，10位的长度最多支持部署1024个节点；
• 最后12位时毫秒内的计数，12位的计数顺序号支持每个节点每毫秒产生4096个ID序列。

雪花算法的优势是生成的ID整体上按照时间趋势递增，稳定性和效率高，但是依赖机器时钟，如果时钟回拨，则可能导致生成的ID重复。但是很多时候一般推荐使用雪花算法避重。

数据迁移、扩容问题

随着数据持续增加分表后还需要进行动态新增表时，这个时候就要考虑数据迁移以及扩容问题。一般做法是先读出历史数据，然后按照指定的分表规则再将数据写入各个分表中。

如果是数值范围分表，只需要添加新的表就可以进行扩容，不需要对原来的分表数据进行迁移，比兔采用日期范围做分表。

如果是数值取模分片，就需要对数据进行迁移以及后续的扩容。最受欢迎的分片规则采用的是跳跃一致性哈希算法，此算法相对于传统的一致性哈希算法有着零内存消耗、均匀分配、快速的优势。如果单纯使用常规的hash算法(基于分区、分表个数取模)，当要增加新的分区、分表的时候，需要对原先的数据重新根据新的取模进行数据迁移。而采用一致性哈希算法之后，需要迁移的数据量很少。

一致性哈希算法也是使用取模的方法，只是不同于常规的hash算法对分区或者分表数进行取模，而是对2^32取模。简单俩说，一致性hash算法将整个哈希空间组织成一个虚拟的圆环：

以上由2^32个点组成的圆环称为hash环，整个空间按照顺时针方向组织。

将各个分表使用hash算法确定各个分表在哈希环上的位置，以四个分表为例子。当需要往表中增加数据的时候，将分片字段使用相同的hash函数计算出哈希值，并且确定数据在哈希环上的位置，从当前位置沿着环顺时针行走，遇到的第一个分表就是该数据将存储到的那个分表。

所以，随着数据量持续增加分表后还需要进行动态新增分表的时候，首先将分表使用相同的hash算法定位到哈希环上，那么仅仅是新表到其环空间中的后一个分表(当前位置沿着顺时针方向行走遇到的第一个分表)之间的数据需要迁移。这样就减少了数据迁移的数量。