逆波兰计算器

逆波兰计算器的实现

1，基本思路

		1，将中缀表达式存入一个集合，方便遍历使用
		2，将中缀表达式，转换为后缀表达式（逆波兰表达式）
		3，使用后缀表达式计算求值

2，具体实现思路

		1，中缀表达式存入集合：
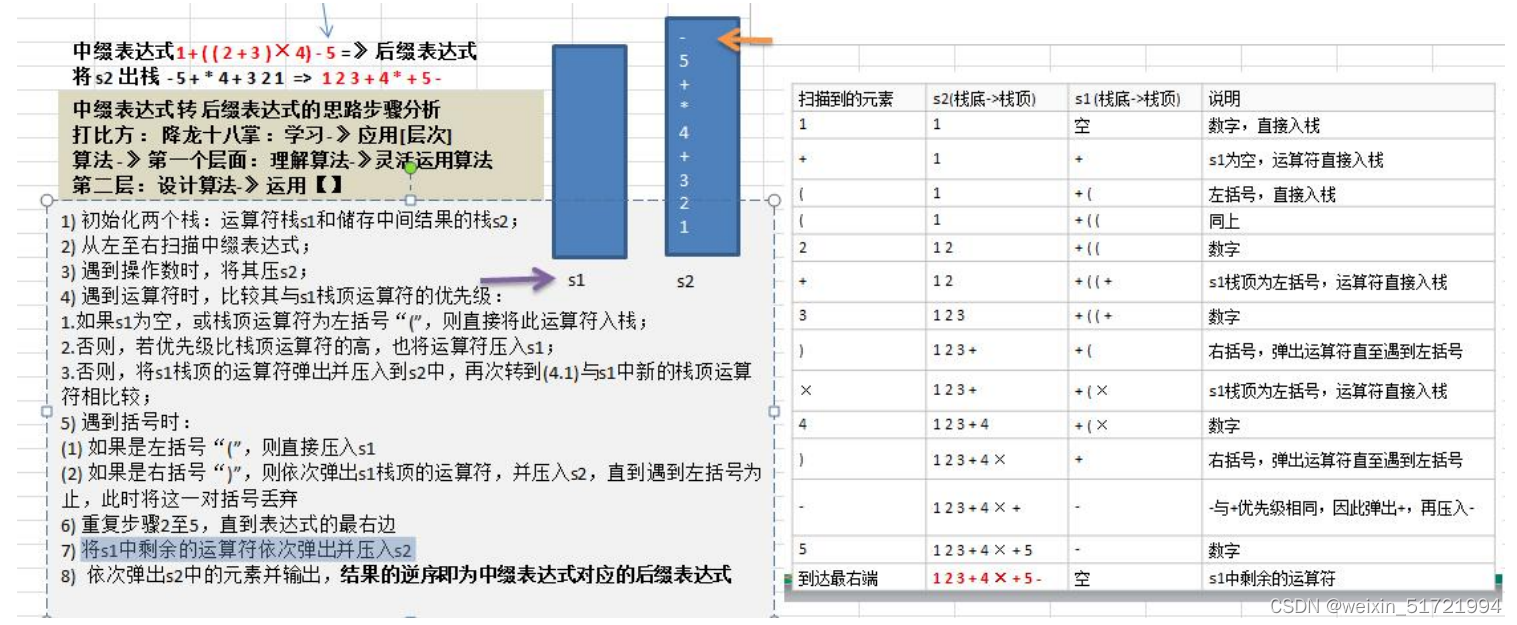
			首先，对字符串从左至右进行遍历，如果遇到符号，则直接存入集合，如果遇到数
			字，则判断是否是多位数，如果是多位数，将多位数存入集合，如果不是多位数，
			直接尺存入集合。

		2，中缀表达式转后缀表达式：

			注意：因为操作数栈数s2没有出栈操作，所以可以使用集合代替，效率更高

		3，使用后缀表达式计算求值：
			首先，从左至右扫描后缀表达式，遇到数字时，将其压入堆栈，遇到运算符时，弹出栈
			顶的两个数，用运算符对他们做相应的计算，并将结果入栈。重复上述过程直至表达式
			最右端。最后栈中的值即为表达式的结果。

3，代码实现

1，计算工具类

package 数据结构.栈.逆波兰计算器;
//计算工具类
public class JSUtils {
    //1，判断运算符的优先级,数字越大，则优先级就越高.
    public static int priority(String oper){
        if(oper.equals("+")||oper.equals("-")){
            return 0;
        }
        else if(oper.equals("*")||oper.equals("/")){
            return 1;
        }
        return -1;
    }

    //2,计算方法
    public static int cal(int num1,int num2,String oper){
        switch (oper){
            case "+":
                return num1+num2;
            case "-":
                return num2-num1;
            case "*":
                return num1*num2;
            case "/":
                return num2/num1;
            default:
                return 0;

        }
    }
}

2，逆波兰表达式的入栈，转换，计算

package 数据结构.栈.逆波兰计算器;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

//逆波兰计算器的实现
public class NiBoLan {

    //1，将中缀表达式存入一个集合
    public  static List<String> zToL(String expression){
        //创建一个集合，存放中缀表达式
        List<String> z=new ArrayList<String>();
        //对字符串进行遍历，将其存入集合
        char c;
        int index;
        String str;
        for(index=0;index<expression.length();){
            //如果当前字符是非数字，则直接存入集合
            if((c=expression.charAt(index))<48||((c=expression.charAt(index))>57)){
                z.add(""+c);
                index++;
            }
            //如果当前字符是数字，则判断是否是多位数
            else{
                //将数字拼接到str中
                str="";
                while (index<expression.length()&&(c=expression.charAt(index))>=48&&(c=expression.charAt(index))<=57){
                    str+=c;
                    index++;
                }
                z.add(str);
            }
        }
        return z;
    }
    //2,将中缀表达式转换为后缀表达式
    public static List<String> zTOH(List<String> z){
        //创建一个集合存放后缀表达式
        List<String> h=new ArrayList<String>();
        //创建一个符号栈
        Stack<String> s=new Stack<String >();
        //从左向右扫描z集合中的中缀表达式
        for (String zh:z) {
            //如果是数字，则直接放到h集合
            if(zh.matches("\\d+")){
                h.add(zh);
            }
            //如果是符号
            //1,如果是左括号(,则直接入符号栈
            else if(zh.equals("(")){
                s.push(zh);
            }
            //2,如果是有括号")"，则将符号栈中的栈顶符号弹出，存入h集合，直到遇见左括号"("
            else if(zh.equals(")")){
                while (!s.peek().equals("(")){
                    h.add(s.pop());
                }
                s.pop();
            }
            //3,如果不是括号，则判断栈是否为空，或者栈顶是否是左括号，若成立，直接入栈，
            //若不成立，比较当前符号和栈顶符号的优先级，如果优先级高，则直接入栈，否则，取出栈顶元素，继续比较
            else {
                //不成立
                while ((!s.isEmpty())&&(!s.peek().equals("("))&&(JSUtils.priority(s.peek())>=JSUtils.priority(zh))){
                    h.add(s.pop());
                }
                //成立，将符号入栈
                s.push(zh);
            }
        }
        //将栈里剩余符号取出
        while (!s.isEmpty()){
            h.add(s.pop());
        }
        return h;
    }

    //计算得出结果
    public static int sum(List<String> h){
        //创建一个栈存放运算结果
        Stack<String> s=new Stack<String>();
        //遍历集合
        for (String ch:h) {
            //如果遇到数字，则将其压入栈
            if(ch.matches("\\d+")){
                s.push(ch);
            }
            //如果遇到符号，则取出栈中前两个数字，运算，将结果存入栈
            else{
                int res = JSUtils.cal(Integer.parseInt(s.pop()), Integer.parseInt(s.pop()), ch);
                s.push(Integer.toString(res));
            }
        }
        return Integer.parseInt(s.pop());
    }
}

3，测试类

package 数据结构.栈.逆波兰计算器;

import java.util.Scanner;

public class Test {
    public static void main(String[] args) {
        Scanner in=new Scanner(System.in);
       while (true){
           System.out.println("请输入计算式：");
           String s=in.next();
           int sum = NiBoLan.sum(NiBoLan.zTOH(NiBoLan.zToL(s)));
           System.out.println(sum);
       }
    }
}