系列简介:这个系列文章讲解线性代数的基础内容,注重学习方法的培养。线性代数课程的一个重要特点(也是难点)是概念众多,而且各概念间有着千丝万缕的联系,对于初学者不易理解的问题我们会不惜笔墨加以解释。在内容上,以国内的经典教材“同济版线性代数”为蓝本,并适当选取了一些补充材料以开阔读者的视野。本系列文章适合作为初学线性代数时的课堂同步辅导,也可作为考研复习的参考资料。文章中的例题大多为扎实基础的常规题目和帮助加深理解的概念辨析题,并有相当数量的历年考研试题。对于一些难度较大或对理解所学知识有帮助的“经典好题”,我们会详细讲解。阅读更多“线性代数入门”系列文章,欢迎关注数学若只如初见!


上一节中我们介绍了利用拆项法计算行列式的方法,本节我们再介绍一种计算高阶行列式的“高级”方法:加边法。这种方法可以看成行列式按行(列)展开的逆用,通常具有较高的技巧性,下面我们通过典型例题来具体介绍。(由于公式较多,故正文采用图片形式给出。)
一、“加边法”概述。

二、利用加边放计算行列式的典型例题。(本题我们在“爪型行列式”一节介绍过,这里介绍的解法是通过“加边”将其转化为“爪型”。)

三、例1的详细解答。
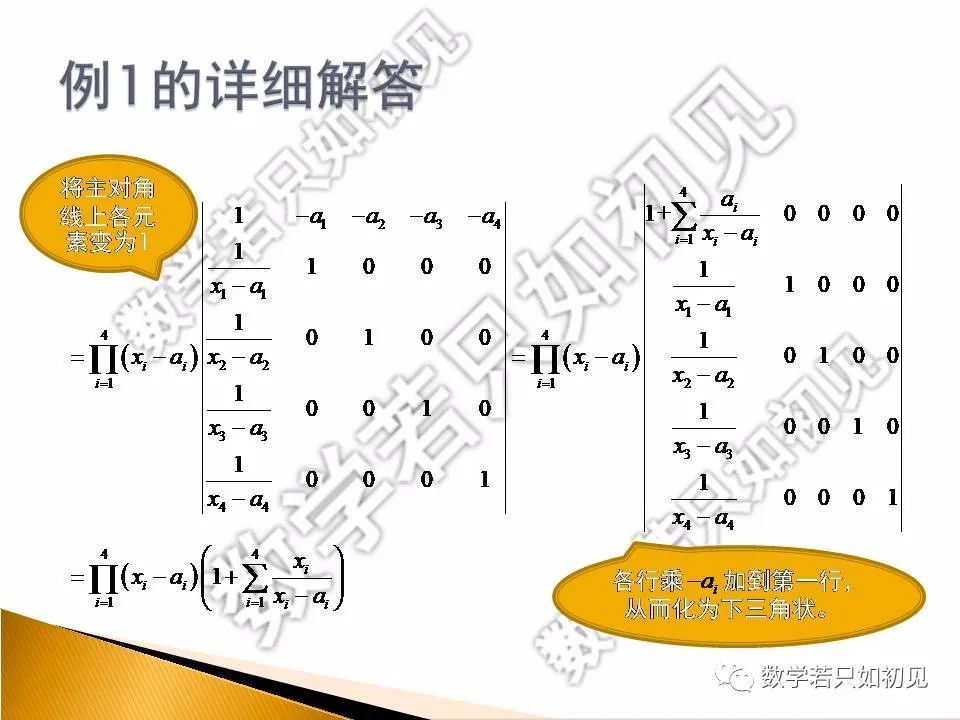
关于“爪型行列式”的定义和计算方法的介绍见下文:
线性代数入门——“爪型行列式”的计算及其应用
四、综合应用多种方法计算行列式的典型例题。

五、例2的详细解答。(本题难度较大,综合运用了加边、拆项等技巧,转化为范德蒙德行列式计算。另外须要注意,在对n阶行列式使用加边法后,得到的是一个n+1阶行列式,在计算过程中不要忘记。)


关于范德蒙德行列式的计算公式见下文:
线性代数入门——范德蒙德行列式的计算及其简单应用
(范德蒙德行列式非常重要,其计算公式必须熟记。)
上一篇:线性代数入门——利用“拆项法”计算行列式
版权声明:本文为weixin_39907220原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。