C语言编程之计算二进制数中1的个数

首先我们利用第一种方法，在这我们可以知道，我们从二进制最小位依次往上看。
例如：5的二进制是101，如果它的二进制最小位上是有数值得，这样我们就对他++，否则，我们就进行移位操作，这部操作当然也可以用除二来代替。
代码如下：

//写一个函数返回参数的二进制中1的个数
#include<stdio.h>
#include<stdlib.h>
int count_one_bits(unsigned int value)
{
    int count = 0;
    while (value != 0)
    {
        if (value % 2 == 1)
        {
            count++;
        }
        value = value >>1;
    }
    return count;
}
int main()
{
    int num;
    int ret;
    printf("请输入一个大于0的数\n");
    scanf("%d", &num);
    ret=count_one_bits(num);
    printf("%d", ret);
    system("pause");
    return 0;
}

第二种方法：我们就利用我们所熟悉的位操作。
我们分析，如果二进制最后一位是1，那么我们采用与运算，如果得到是1，那个就得出有一个1，否则，进行移位操作。
代码如下：

//第二种方法，进行位操作的方法
#include<stdio.h>
#include<stdlib.h>
int count_one_bits(unsigned int value)
{
    int count = 0;
    while(value)
    { 
        if (value & 1 == 1)
        {
            count++;
            value >>= 1;
        }
        else
            value >>= 1;


    }
    return count;
}
int main()
{
    int num;
    int ret;
    printf("请输入一个大于0的数\n");
    scanf("%d", &num);
    ret = count_one_bits(num);
    printf("%d", ret);
    system("pause");
    return 0;
}

第三种方法： 采用减1再进行与的运算，这样每进行一次，就会少一个1.

//第二种方法，进行位操作的方法
#include<stdio.h>
#include<stdlib.h>
int count_one_bits(unsigned int value)
{
    int count = 0;
    while(value)
    { 
        value=value&value - 1;
        count++;

    }
    return count;
}
int main()
{
    int num;
    int ret;
    printf("请输入一个大于0的数\n");
    scanf("%d", &num);
    ret = count_one_bits(num);
    printf("%d", ret);
    system("pause");
    return 0;
}

在这里我补充一种我在牛客网刷题得到的一种平行算法。

int BitCount(unsigned int n)
{
    n = (n &0x55555555) + ((n >>1) &0x55555555) ;
    n = (n &0x33333333) + ((n >>2) &0x33333333) ;
    n = (n &0x0f0f0f0f) + ((n >>4) &0x0f0f0f0f) ;
    n = (n &0x00ff00ff) + ((n >>8) &0x00ff00ff) ;
    n = (n &0x0000ffff) + ((n >>16) &0x0000ffff) ;

    return n ;
}

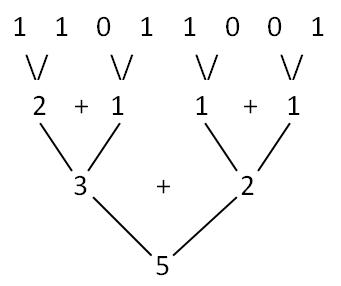
速度不一定最快，但是想法绝对巧妙。 说一下其中奥妙，其实很简单，先将n写成二进制形式，然后相邻位相加，重复这个过程，直到只剩下一位。

以217（11011001）为例，有图有真相，下面的图足以说明一切了。217的二进制表示中有5个1