目录
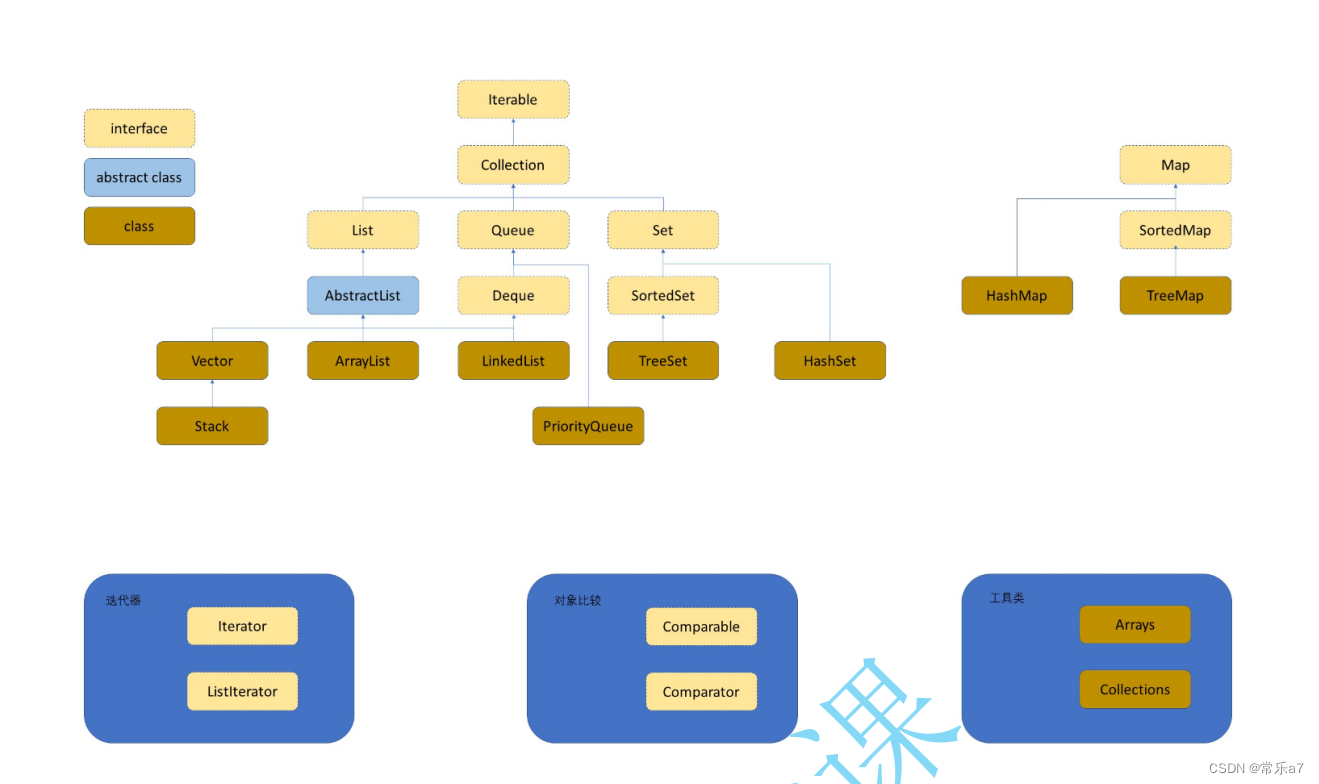
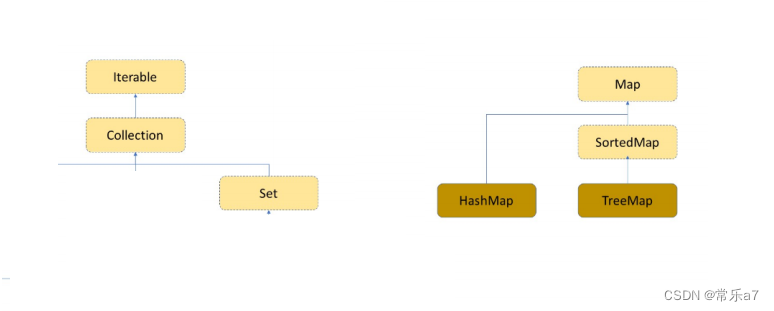
3.1 继承体系(因为继承于Iterable接口，可以使用增强for循环和迭代器进行遍历)
4.1 继承体系(Map不同于Set，因为没继承Iterable接口不能直接遍历)
4.4 与Collection(集合)的联系（转换之后，可以遍历了）
1 整题把握
本文主要是介绍关于搜索的数据结构，包含搜索树，哈希表，以及Set和Map两类接口，下图可以帮助读者掌握他们之间的基本联系，后问有更详细的介绍。
2 搜索分类
2.1 静态数组
- 直接遍历，时间复杂度为O(N)，元素如果比较多效率会非常慢
- 二分查找，时间复杂度为O(log2N),但搜索前必须要求序列是有序的
上述排序比较适合静态类型的查找，即一般不会对区间进行插入和删除操作了。而对于动态查找，需要用到Set和Map类的数据结构。
2.2 搜索树
2.2.1 概念
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
1）若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
2）若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
3）它的左右子树也分别为二叉搜索树
2.2.2 模型 （key值不允许重复）
- 纯key模型 Set下的TreeSet 时间复杂度为O(log2N)
- key—value模型 Map下的TreeMap 时间复杂度为O(log2N)
2.2.3 常用方法 (纯Key模型实现)
前提：三个方法中，都要比较key值大小，因此K类型应该具备比较大小的能力。
查找操作：booleans contains(Object key)
public boolean contains(long key) {
// 整个过程只需要维护根结点root和size即可
// 下面用了大于和小于等比较关系，因此key是必须具备比较的能力，这里基本类型是具备的
TreeNode cur=root;
while(cur!=null){
if(cur.key<key){
cur=cur.left;
}else if(cur.key>key){
cur=cur.right;
}else{
return true;
}
}
return false;
}插入操作：booleans add(Object key)
public boolean add(long key) {
TreeNode cur=root;
// 要插入的结点node
TreeNode node=new TreeNode(key);
if(cur==null){
// 初始根结点为null，插入的结点变成新的根结点
root=node;
this.size++;
return true;
}
// 记住遍历当前结点的前一个街结点
TreeNode prev=null;
// 为了保证树的结构不变，插入新key结点的地方必须某个根结点孩子的位置
while (cur!=null){
if(key>cur.key){
prev=cur;
cur=cur.right;
}else if(key<cur.key){
prev=cur;
cur=cur.left;
}else{
// 找到了重复的key值，插入失败
return false;
}
}
// 循环结束找到了要插入的地方，要插入，一定要有前一个结点
// 循环中相等的情况已经返回,程序走到这里，说明肯定不会相等
// 另外prev!=null
// 判断插入的是左孩子还是右孩子
if(key<prev.key){
prev.left=node;
}else{
prev.right=node;
}
this.size++;
return true;
}删除操作：booeans remove(Object key)
private void deleteNode(TreeNode prev, TreeNode cur) {
// 分类讨论
// 1） cur没有孩子
// 2） cur有一个孩子
// 3） cur有两个孩子
// 因为要维护root，可能cur是root
// 所以以上三种情况都要考虑cur是否是root,也就是prev是否为null
if(cur.left==null&&cur.right==null){
// cur没有孩子的情况
if(prev==null){
// cur是根结点,并且树中只有根结点
root=null;
}else if(prev.left==cur){
// cur是prev的左孩子
prev.left=null;
}else{
// cur是prev的右孩子
prev.right=null;
}
}else if(cur.left!=null&&cur.right==null){
// cur有左孩子没有右孩子
if(prev==null){
// cur是根结点,新的根结点变成了cur的左孩子
root=cur.left;
}else if(prev.left==cur){
// cur是prev的左孩子
prev.left=cur.left;
}else{
// cur是prev的右孩子
prev.right=cur.left;
}
}else if(cur.left==null&&cur.right!=null){
// cur有右孩子没有左孩子
if(prev==null){
// cur是根结点,新的根结点变成了cur的右孩子
root=cur.right;
}else if(prev.left==cur){
// cur是prev的左孩子
prev.left=cur.right;
}else{
// cur是prev的右孩子
prev.right=cur.right;
}
}else{
// cur有两个孩子
// 不用考虑cur是否为根结点的情况，因此cur不会变，只是它的值会改变
// 去找到合适的结点代替要删除的结点
// 两种选择，一是找左子树中最大的(即左子树最右边的孩子)，二是找右子树中最小的(即右子树最左边的孩子)
// 这里选择右子树中最小的替换删除
TreeNode deleteNodeParent=cur;
// cur一定非null，所以deleteNodeParent也是非null
TreeNode deleteNode=cur.right;
while (deleteNode.left!=null){
// 一直往右找，直到某次左孩子为null，表示找到了合适的
deleteNodeParent=deleteNode;
deleteNode=deleteNode.left;
}
// 替换删除，改变原先要删除结点的key值
cur.key=deleteNode.key;
// deleteNode变成要删除的结点，因此要记录它的父节点
// deleteNodeParent一定非null
// 而正好当上述循环一次不走的时候dn是dp的右孩子，其他情况都是左孩子
if(deleteNodeParent.left==deleteNode){
// 让要dn的父节点dp指向自己的孩子(因为是右子树中最左边的，因此孩子只能是右孩子)
deleteNodeParent.left=deleteNode.right;
}else {
deleteNodeParent.right=deleteNode.right;
}
return;
}
}2.2.4 和Java类集（Set、Map）的关系
2.3 哈希表
2.3.1 概念
搜索方法：
不经过任何比较，一次直接从表中得到要搜索的元素。 如果构造一种存储结构，通过某种函 数(hashFunc)使元素的存储位置(位置下标)与它的关键码(key)之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素。
哈希函数与哈希表：
哈希方法中使用的转换函数称为哈希(散列)函数，构造出来的结构称为哈希表(Hash Table)(或者称散列表)。
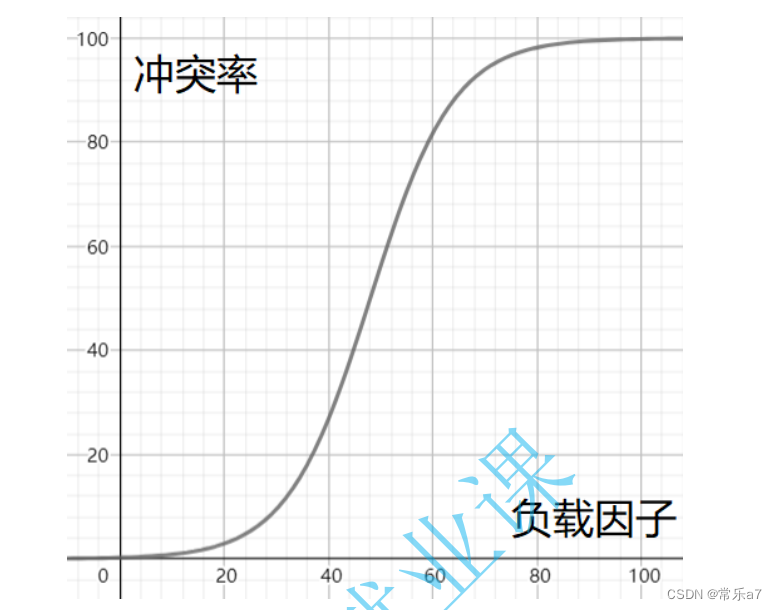
哈希冲突：
对于两个数据元素的关键字 i != j，
但有：
Hash( ) == Hash( )
，即：
不同关键字通过相同哈
希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。
但有：
Hash( ) == Hash( )
，即：
不同关键字通过相同哈
希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。
哈希冲突的避免：
1）哈希函数的设计
- 哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值域必须在0到m-1 之间
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单
常见的哈希函数:直接定制法、除留余数法
2）负载因子调节
所以当冲突率达到一个无法忍受的程度时，我们需要通过降低负载因子来变相的降低冲突率。
已知哈希表中已有的关键字个数是不可变的，那我们能调整的就只有哈希表中的数组的大小。
哈希冲突的解决：
- 闭散列：线性探测/二次探测
- 开散列：哈希桶（开链法）
2.3.2 模型 （key值不允许重复）
- 纯key模型 Set下的HashSet 时间复杂度为O(1)
- key—value模型 Map下的HashMap 时间复杂度为O(1)
2.3.3 实现(纯key模型)
同上述搜索树的三个方法
public class HashTableSet {
// 模型纯key模型的哈希表，即类型HashSet
static class ListNode{
long key;
ListNode next;
public ListNode(long key){
this.key=key;
}
}
public HashTableSet(){
array=new ListNode[7];
this.size=0;
}
// 维护数组和多条链表，每个数字的元素都是一条链表（这里用头结点表示）
private ListNode[] array;
private int size;
public boolean contains(long key){
// 1.使用哈希函数，将key转换为下标
int index=hashCode(key);
// 2.把key值转换为下标，确定链表的位置
ListNode head=array[index];
// 3.遍历当前位置下的链表
ListNode cur=head;
// 该循环的时间复杂度是O(n)，其中n是链表的长度，依据统计规律(泊松分布)，基本上链表长度不可能超过8
while (cur!=null) {
if(cur.key==key){
return true;
}
cur=cur.next;
}
//
return false;
}
public boolean add(long key){
// 1.使用哈希函数，将key转换为下标
int index=hashCode(key);
// 2.把key值转换为下标，确定链表的位置
ListNode head=array[index];
// 3.遍历当前位置下的链表
ListNode cur=head;
// 4.因为Set不能重复插入，因此需要先遍历每条链表，判断是否已经有了key值
while (cur!=null){
if(cur.key==key){
return false;
}
cur=cur.next;
}
// 循环结束，该位置的链表中不包含，将这个key值插入到链表中
// 头插、尾插都可以，这里为了方便实现，采用头插,注意是插到数组某个位置
ListNode node=new ListNode(key);
// 不能写成
// node.next=head;
// head=node;
node.next=array[index];
array[index]=node;
this.size++;
return true;
// TODD 没有考虑有负载因子过大，导致需要扩容的情况
}
public boolean remove(long key){
// 1.使用哈希函数，将key转换为下标
int index=hashCode(key);
// 2.把key值转换为下标，确定链表的位置
ListNode head=array[index];
// 链表不存在的情况
if(head==null){
return false;
}
// 头删的情况
if(head.key==key){
array[index]=null;
this.size--;
return true;
}
// 3.遍历当前位置下的链表，并记录其前驱结点
ListNode prev=head;
ListNode cur=head.next;
while (cur!=null){
if(cur.key==key){
prev.next=cur.next;
this.size--;
return true;
}
prev=cur;
cur=cur.next;
}
// 没有找到key值结点，删除失败
return false;
}
public static void main(String[] args) {
HashTableSet hashTableSet=new HashTableSet();
hashTableSet.add(0);
hashTableSet.add(3);
hashTableSet.add(7);
hashTableSet.add(9);
}
private int hashCode(long key) {
return (int)key%7;
}
}2.3.4 put操作
- key变成int类型，通过key.hashCode()，因此key类型需要重写hashCode()
- int -> 合法下标 官方做法：(n-1)&hash 前提n是2的倍数
- 找到对应链表进行比较，通过key.equals()，因此key类型需要重写equals()
- 找到了，更新value；没找到，插入( 头插O(1)更方便，尾插也可以)，官方使用尾插
3 Set
3.1 继承体系(因为继承于Iterable接口，可以使用增强for循环和迭代器进行遍历)
3.2 模型
Set是数学上集合(key值不允许重复)的意思，是一种纯key模型。
3.3 常用方法
3.4 顺序
Set不同于LIst,没有位置下标的概念。
- TreeSet(搜索树) 是中序有序的
- HashSet(哈希表)无序
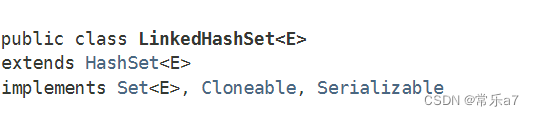
3.5 LinkedHashSet
不同于TreeSet，LinkedHashSet可控制顺序是插入顺序，因此在某些题中需要达到按顺序+去重的效果时，可以使用这种数据结构。
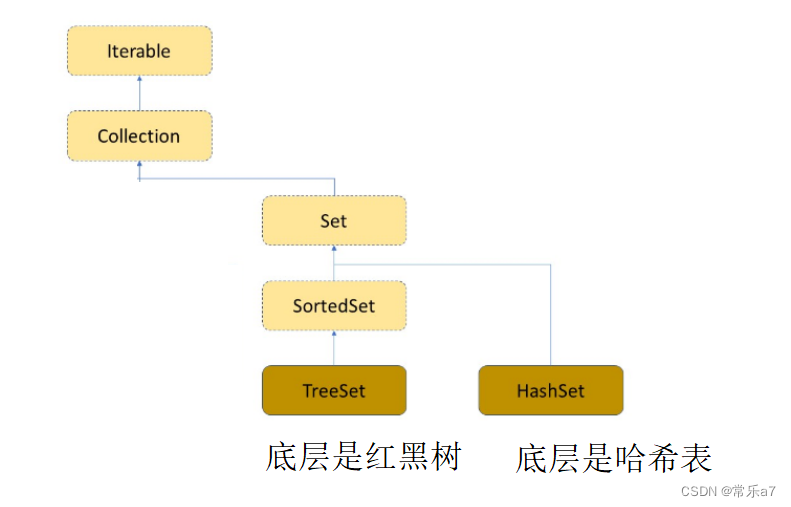
3.6 TreeSet与HashSet
3.7 遍历方式
- 直接遍历Set集合(容器),使用增强for循环
- 调用Iterator方法，使用迭代器，hasNext() 方法+next()方法
4 Map
4.1 继承体系(Map不同于Set，因为没继承Iterable接口不能直接遍历)
4.2 模型
Map表示映射，构建了一种一对一或多对一的函数关系，即key-value模型，key不能重复，value可以重复。
4.3 常用方法
4.4 与Collection(集合)的联系（转换之后，可以遍历了）
- Set<K> keySet()
- Collection values
- Set<Map.Entry<K,V>> entrySet()
其中Map.Entry<K,V> 主要的方法
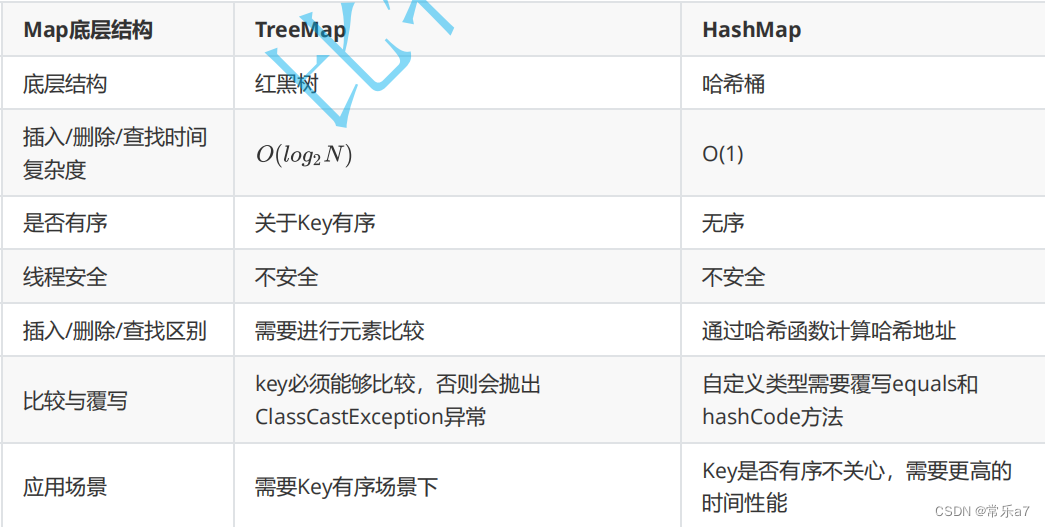
4.5 TreeMap和HashMap
5 总结
5.1 Set与Map的区别
- 主要是模型不同，Set是纯key模型，Map是key-value模型，两种key值都不能重复
- 常用方法上 插入 搜索树 add() —》 哈希表 put()
- Set可以遍历，Map不能直接遍历
5.2 搜索树和哈希表
- 实现角度：哈希表实现更简单(更容易实现线程安全)
- 性能上： 搜索树 O(log2N) 哈希表 O(1)
- 顺序上： 搜索树关于key中序有序，支持范围查找 哈希表无序，只支持等于和不等于查找
- 要求上： 搜索树要求key具备可比较的能力 哈希表要求key类型(自定义)重写equals方法和hashCode方法
- 底层结构： 搜索树 红黑树 哈希表 数组+链表+红黑树
版权声明：本文为m0_66071933原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。