如何有效地求自然数的幂和
伯努利数 (Bernoulli numbers)是什么?
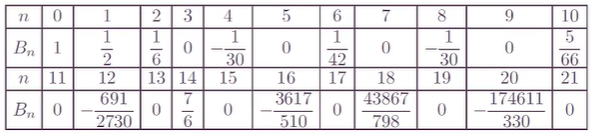
伯努利数不是一个常数,而是一串数列 B0 = 1, B1 = 1 / 2, B2 = 1 / 6, …
递推法
求自然数的幂和方法有很多种,首先是普通的递推求法:
基于二项式定理,我们有
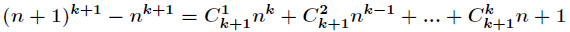
a2 – b 2 = (a – b) · (a + b)
a3 – b 3 = (a – b) · (a2 + ab + b2)
a4 – b 4 = (a – b) · (a3 + a2b + ab2 + b3)
…
那么对于所有的 n = 1, 2, 3, … 累加得到
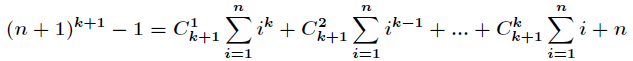
移项整理得:
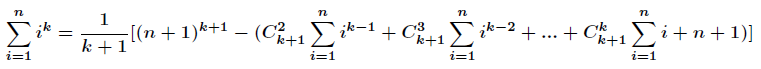
可以看出这是一个递推式,如果我们记
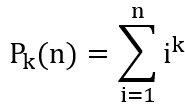
那么得到如下递归式
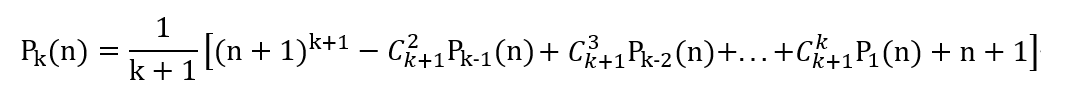
递归出口是 k == 1
P1(n) = 1 + 2 + … + n = n · (n + 1) / 2
为了提高效率,在递归的时候需要记忆化
上面的式子还能再简化吗,我不知道,既然没有什么想法,那么我们试着将上面的推导进行推广
(n + 1)k – 1k+1 中 n + 1 换成 n + 2, 或者 n + 3 可不可以,不如用一个m来表示 (n + m)k
让n取1, 2,…,n,则
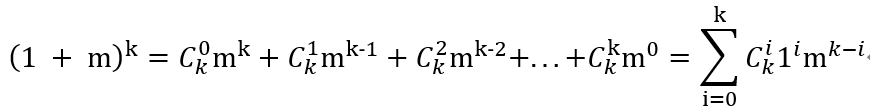
…
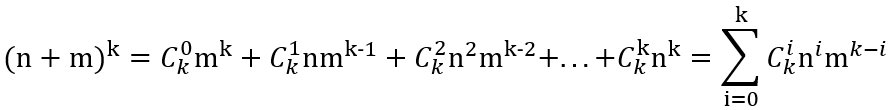
将上面的式子进行累加得:
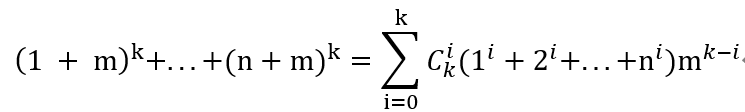
用之前的记号简写为:
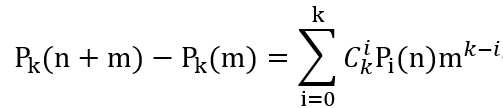
这里对n进行求导,因为把n作为变量,把m作为常量的话,就可以把Pk(m)消掉了
对变量n两边同时求导就有
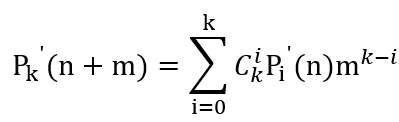
把n = 0 代入就有
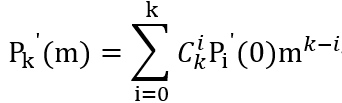
这样子就可以得到一个Pk的导数的简单的表达式,这就和我们想要的差不多了,我们想知道Pk(m)的导数表达式,我们只需要把它们在原点处的导数算出来即可,因为是多项式,所以在原点处的导数不就是Pi的一次项系数吗
因为我们的目标是要把Pk表示出来,两边同时积分不就可以了?
两边对m从0到n求积分有
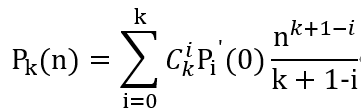
我们记
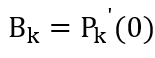
数列一般是有通式,但有些像斐波那契数列则是给出递推关系式
我们想找到B0,B1,B2,…的递推式,然后再用这个递推式来定义Pk(n)这串数列,这样才方便计算
根据先前的讨论
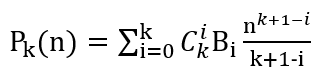
把n = 1代入得:
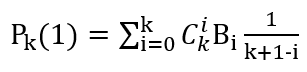
根据组合数得性质:
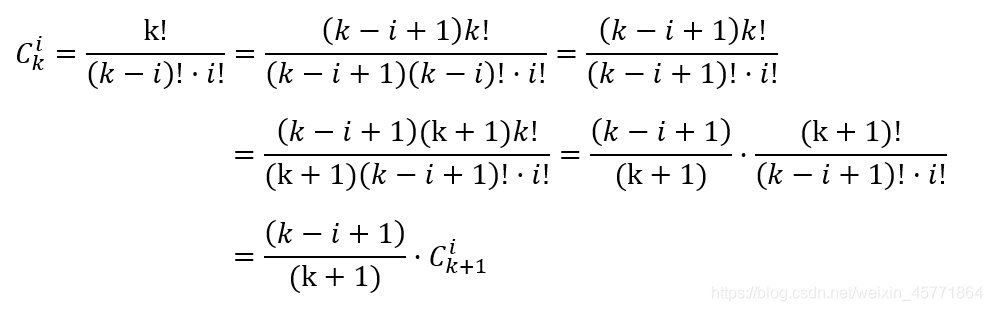
整理得:
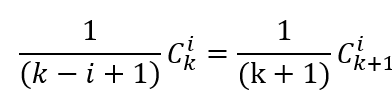
故:
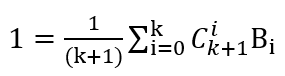
我们把Bk提取出来:
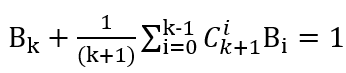
整理得:
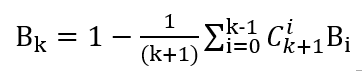
这就是我们要的递推关系式了:
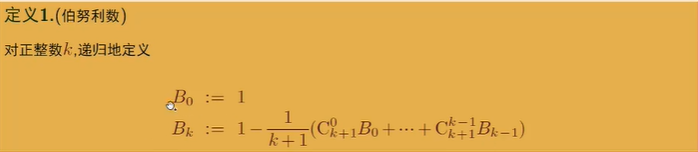
因此也可以推导出Pk(n)
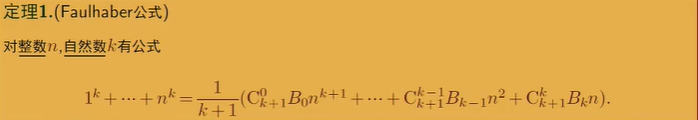
今天先更到这里…