一、雅各比
雅各比矩阵式多元形式的导数,假设有以下3个函数,每个函数有6个自变量:
y
1
=
f
1
(
x
1
,
x
2
,
x
3
)
y
2
=
f
2
(
x
1
,
x
2
,
x
3
)
y
3
=
f
3
(
x
1
,
x
2
,
x
3
)
\begin{aligned} &y_1 = f_1(x_1, x_2, x_3) \\ \\ &y_2 = f_2(x_1, x_2, x_3) \\\\ &y_3 = f_3(x_1, x_2, x_3) \end{aligned}
y1=f1(x1,x2,x3)y2=f2(x1,x2,x3)y3=f3(x1,x2,x3)
写成矩阵的形式:
Y
=
F
(
x
)
Y = F(x)
Y=F(x)
其中:
Y
=
[
y
1
y
2
y
3
]
X
=
[
x
1
x
2
x
3
]
Y = \begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix} \quad X = \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}
Y=⎣⎡y1y2y3⎦⎤X=⎣⎡x1x2x3⎦⎤
计算
y
i
y_i
yi的微分与
x
i
x_i
xi的微分的函数:
δ
y
1
=
∂
f
1
∂
x
1
δ
x
1
+
∂
f
1
∂
x
2
δ
x
2
+
∂
f
1
∂
x
3
δ
x
3
δ
y
2
=
∂
f
2
∂
x
1
δ
x
1
+
∂
f
2
∂
x
2
δ
x
2
+
∂
f
2
∂
x
3
δ
x
3
δ
y
3
=
∂
f
3
∂
x
1
δ
x
1
+
∂
f
3
∂
x
2
δ
x
2
+
∂
f
3
∂
x
3
δ
x
3
\begin{aligned} &\delta y_1 = \frac{\partial f_1}{\partial x_1}\delta x_1 +\frac{\partial f_1}{\partial x_2}\delta x_2 + \frac{\partial f_1}{\partial x_3}\delta x_3 \\\\ &\delta y_2 = \frac{\partial f_2}{\partial x_1}\delta x_1 +\frac{\partial f_2}{\partial x_2}\delta x_2 + \frac{\partial f_2}{\partial x_3}\delta x_3 \\\\ &\delta y_3 = \frac{\partial f_3}{\partial x_1}\delta x_1 +\frac{\partial f_3}{\partial x_2}\delta x_2 + \frac{\partial f_3}{\partial x_3}\delta x_3 \\\\ \end{aligned}
δy1=∂x1∂f1δx1+∂x2∂f1δx2+∂x3∂f1δx3δy2=∂x1∂f2δx1+∂x2∂f2δx2+∂x3∂f2δx3δy3=∂x1∂f3δx1+∂x2∂f3δx2+∂x3∂f3δx3
写成矩阵形式:
[
δ
y
1
δ
y
2
δ
y
3
]
=
[
∂
f
1
∂
x
1
∂
f
1
∂
x
2
∂
f
1
∂
x
3
∂
f
2
∂
x
1
∂
f
2
∂
x
2
∂
f
2
∂
x
3
∂
f
3
∂
x
1
∂
f
3
∂
x
2
∂
f
3
∂
x
3
]
[
δ
x
1
δ
x
2
δ
x
3
]
\begin{bmatrix}\delta y_1\\\\\delta y_2\\\\\delta y_3\end{bmatrix} = \begin{bmatrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\frac{\partial f_1}{\partial x_3}\\\\\frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\frac{\partial f_2}{\partial x_3}\\\\ \frac{\partial f_3}{\partial x_1}&\frac{\partial f_3}{\partial x_2}&\frac{\partial f_3}{\partial x_3}\end{bmatrix} \begin{bmatrix}\delta x_1\\\\\delta x_2\\\\\delta x_3\end{bmatrix}
⎣⎢⎢⎢⎢⎡δy1δy2δy3⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎡∂x1∂f1∂x1∂f2∂x1∂f3∂x2∂f1∂x2∂f2∂x2∂f3∂x3∂f1∂x3∂f2∂x3∂f3⎦⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡δx1δx2δx3⎦⎥⎥⎥⎥⎤
即:
δ
Y
=
∂
F
∂
X
δ
X
\delta Y = \frac{\partial F}{\partial X}\delta X
δY=∂X∂FδX
这里的
∂
F
∂
X
\frac{\partial F}{\partial X}
∂X∂F就是雅各比矩阵,记为
J
(
X
)
J(X)
J(X)。对上式两边同时乘时间的微分
δ
t
\delta t
δt,得到:
Y
˙
=
J
(
X
)
X
˙
\dot Y = J(X)\dot X
Y˙=J(X)X˙
二、两轴机械臂
以上述两自由度机械臂为例。我们如何求解关节角速度与机械臂末端的关系呢
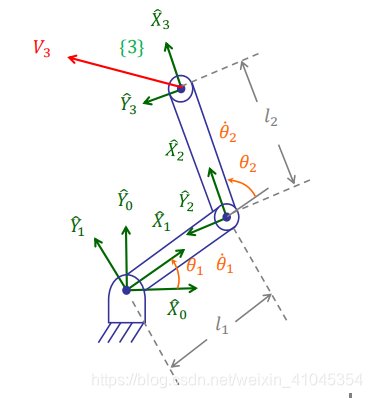
方法一:迭代法求解
我们根据各关节角速度,求解
V
3
,
V_3,
V3,其变换矩阵依次为:
1
0
T
=
[
c
1
−
s
1
0
0
s
1
c
1
0
0
0
0
1
0
0
0
0
1
]
^0_1T = \begin{bmatrix} c_1 & -s_1 & 0 & 0\\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}
10T=⎣⎢⎢⎡c1s100−s1c10000100001⎦⎥⎥⎤
2
1
T
=
[
c
1
−
s
1
0
l
1
s
1
c
1
0
0
0
0
1
0
0
0
0
1
]
^1_2T = \begin{bmatrix} c_1 & -s_1 & 0 & l_1\\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}
21T=⎣⎢⎢⎡c1s100−s1c1000010l1001⎦⎥⎥⎤
3
2
T
=
[
1
0
0
l
2
0
1
0
0
0
0
1
0
0
0
0
1
]
^2_3T = \begin{bmatrix} 1 & 0 & 0 & l_2\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}
32T=⎣⎢⎢⎡100001000010l2001⎦⎥⎥⎤
我们可以依次计算其线速度,角速度,由于坐标系
0
{0}
0是固定在地面上的,因此:

转换到
0
{0}
0坐标系下:

至此,我们求解出关节速度与执行器末端线速度的关系。
方法2
根据机械臂的正运动学模型,在已知
θ
1
,
θ
2
\theta_1, \theta_2
θ1,θ2的情况下,可以通过下式求P[x,y]位置:
x
=
L
1
cos
θ
1
+
L
2
c
o
s
(
θ
1
+
θ
2
)
x = L_1\cos\theta_1+ L_2cos(\theta_1 + \theta_2)
x=L1cosθ1+L2cos(θ1+θ2)
y
=
L
1
sin
θ
1
+
L
2
sin
(
θ
1
+
θ
2
)
y = L_1\sin\theta_1 + L_2\sin(\theta_1 + \theta_2 )
y=L1sinθ1+L2sin(θ1+θ2)
其雅各比矩阵为:
J
(
Θ
)
=
[
∂
x
∂
θ
1
∂
x
∂
θ
2
∂
y
∂
θ
1
∂
x
∂
θ
2
]
J(\Theta) = \begin{bmatrix}\frac{\partial x}{\partial \theta_1}&\frac{\partial x}{\partial \theta_2}\\\\\frac{\partial y}{\partial \theta_1}&\frac{\partial x}{\partial \theta_2} \end{bmatrix}
J(Θ)=⎣⎡∂θ1∂x∂θ1∂y∂θ2∂x∂θ2∂x⎦⎤
因此:
[
x
˙
y
˙
]
=
J
(
Θ
)
[
θ
˙
1
θ
˙
2
]
\begin{bmatrix}\dot x\\\\\dot y\end{bmatrix} = J(\Theta)\begin{bmatrix}\dot \theta_1\\\\\dot \theta_2\end{bmatrix}
⎣⎡x˙y˙⎦⎤=J(Θ)⎣⎡θ˙1θ˙2⎦⎤