MATLAB实现CRC校验码的计算

循环冗余校验(cyclicredundancy check,CRC)对传输序列进行一次规定的除法操作，将除法操作的余数附加在传输信息的后面。在接收端，也对收到的数据做相同的除法。如果接收端除法得到的结果其余数不是零，就表明发生了错误。

循环冗余校验是将要发送的数据位序列当作一个多项式f(x)的系数，f(x)的系数只有1与0两种形式。在发送方用收发双方预定的约定的生成多项式G(x)去除，求得一个余数多项式。将余数多项式加到数据多项式之后发送到发送端。这里的除法是错位不减的模2减法，相当于异或运算。接收端采用同样的生成多项式G(x)去除接收到的数据多项式f'(x),如果传输无差错，则接收端除法运算f'(x)/G(x)的结果，其余数为零。否则就认为出现了差错。

基于除法的循环冗余校验，其计算量大于奇偶与求和校验，其差错检测的有效性也比较高，它能够检测出大约99.95%的错误。

程序流程图

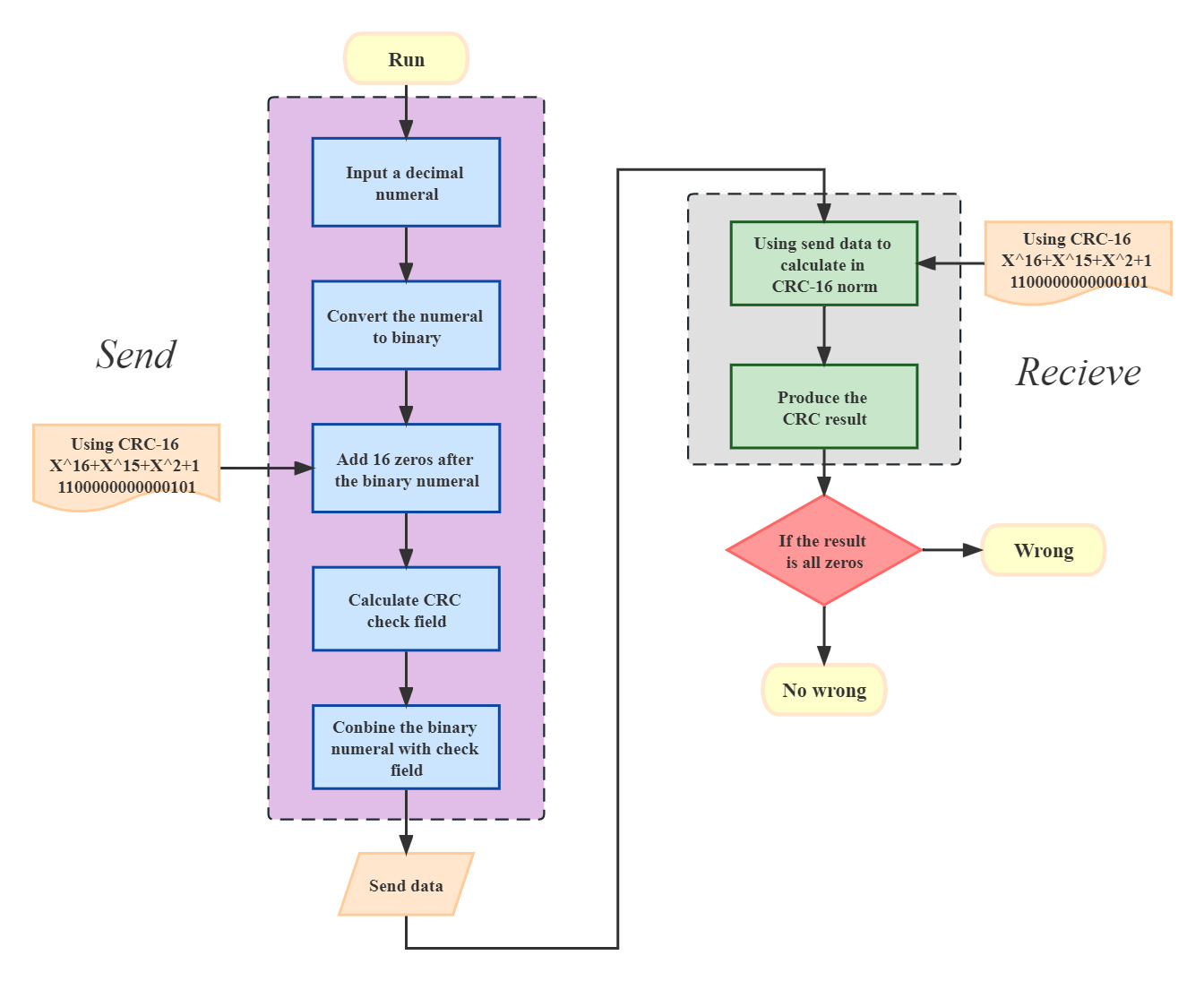
MATLAB程序

本文程序以CRC-16 （X^16+X^15+X^2+1）为例

%输入想要转化的数据
data1=input('Please input the num U want to transform:');

%将十进制数转化成二进制数输出
dec=[];
i=1;
while(data1)
    if mod(data1,2)
     dec=[1,dec];
    else
     dec=[0,dec];
    end
    data1=(data1-mod(data1,2))./2;
end
disp('The below is your num in binary system')
display(num2str(dec))

% 校验多项式CRC-16
polynomial = [1,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1]; 

%进行异或运算
lpol= length(polynomial);
data_dec=dec;
lnum=length(data_dec);
data=[data_dec,zeros(1,lpol-1)];
lpol= length(polynomial);
n=find(data==1,1);
while n<=lnum
for i=1:lpol
    if polynomial(i)==data(n+i-1)
        data(n+i-1)=0;
    else
        data(n+i-1)=1;
    end
end
n=find(data==1,1);
end

%拼接计算结果并显示
result=[data_dec,data(lnum+1:end)];
disp('The polynomial used to CRC is X^16+X^15+X^2+1')
disp('The transform result is')
disp(num2str(result))

%进行结果校验
result2=result;
n=find(result2==1,1);
while n<lnum+lpol-1
for i=1:lpol
    if polynomial(i)==result2(n+i-1)
        result2(n+i-1)=0;
    else
        result2(n+i-1)=1;
    end
end
n=find(result2==1,1);
end
disp('The CRC result is')
disp(num2str(result2))

代码运行效果

Please input the num U want to transform:20201503113

The below num is your num in binary system

1 0 0 1 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 1 1 1 1 0 0 1 1 0 0 0 1 0 0 1

The polynomial used to CRC is X^16+X^15+X^2+1

The transform result is

1 0 0 1 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 1 1 1 1 0 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 1 0 1 0 0 1 0 1 1 0 1

The CRC result is

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0