引子
信息是什么?
在香农的划时代论文发表前,我们对“信息”这个词的含义只有一个模糊的概念。香农针对“信息”给出了一个令人信服的定义,并且说明了如何对信息进行定量计算,并对这个定义给出了数学证明。之后,我们对“信息”的识别、传输、存储、加工等才有了坚实的数学基础;有了坚实的数学基础,才发展出各种工程应用。
因此,毫不夸张,信息论是计算机科学的基石理论之一。
信息熵
香农对信息的定义:信息是不确定性减少的度量。换句话说,“信息”,能减少事物的不确定性;如果一个“信息”对事物不确定性的减少没有任何作用,那么这个“信息”的信息量是0。
我非常喜欢这个定义。它如此简洁美妙、直指本质,简直已经超越数学,向哲学领域进军。香农真是划时代的天才。
以上只是定性的描述。更伟大的是,香农还给出了定量的计算公式:
信息熵H(X)= -Σp(x) logp(x)
其中p(x)是某件事情发生的概率。(这句话相对好理解但不够严谨,更严谨的说法应为p(x)是x的概率质量函数)
同时香农在论文中给出了证明,为什么信息熵公式应该是对数,应该是这个表达式。
以下为香农的证明,相对枯燥,对数学不感兴趣的可以跳过这段,直接看后面结论。
现有一系列随机事件 p1,p2,…,pn的集合,它们发生的概率已知。假设存在一个能反映事件被选择的结果的不确定度的度量 H(p1,p2,…,pn),那么它应该满足下列性质:
1.H 应该连续于pi;
2.若所有 pi 相等(都等于 1/n ),则 H应该是 n 的单调递增函数(当可候选的事件数越多,不确定度相应地也越大)
3.若其中一个选择被分解为两个连续的子选择,那么原始的 H 值应该为分解后的 H 值的加权平均和。图片说明如下:(截图自香农的论文)
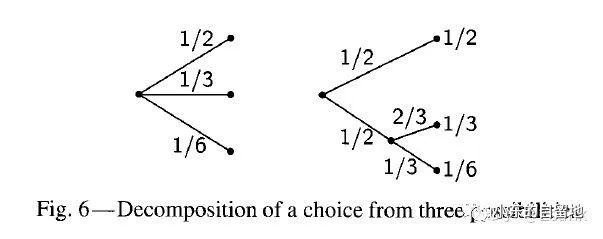
H(1/2,1/3,1/6)=H(1/2,1/2)+1/2H(2/3,1/3)
证明:令 H(1/n,1/n,…,1/n)=A(n)
根据条件3,从事件集合 s中一次选择 m个事件 sm等价于从 s中选择 m次一个事件:
A(sm)=mA(s)
同理,有
A(tn)=nA(t)
令 n 足够大,我们能找到一个 m 满足 sm≤tn<sm+1
取对数:m/n≤logt/logs≤(m/n+1/n)
|m/n-logt/logs|<α
其中α是任意小的数。
由 A(n)的单调性:
A(sm)≤A(tn)≤A(sm+1)
mA(s) ≤nA(t) ≤(m+1)A(s)
同时除以 nA(s):
m/n≤A(t)/ A(s)≤(m/n+1/n)
|m/n- A(t)/ A(s)|<α
| A(t)/ A(s)- logt/logs|<2α
注意到α是任意小的数,因此2α也是任意小的数。
故A(t)=Klogt
前面是基于等概率求得的。现在假设我们依然从 n个事件里选取事件,但这次不再是等概率了,第 i个事件被选取的概率为 pi=ni/Σni。再一次使用性质3,将从总共有 Σni中可能的事件集中一次选取 n个事件分解为以概率 pi,…,pn 选取 n 次,且第 i 个被选取后,从 ni中选取是等概率的,那么有:
KlogΣni=H(p1,…,pn)+KΣpilogni
H=K[ΣpilogΣni-Σpilogni] = -Kσpilog(ni/Σni)= -Kσpi logpi
(非等概率的这部分证明其实没有完全看明白,暂时先记到这里吧。)
至此,得证。
以上的数学证明,简化一下是这样子的:
如果我们把信息定义为一个度量H。并且H满足如下性质:
①H 应该连续于pi;②若所有 pi 相等(都等于 1/n ),则 H应该是 n 的单调递增函数(当可候选的事件数越多,不确定度相应地也越大);③若其中一个选择被分解为两个连续的子选择,那么原始的 H 值应该为分解后的 H 值的加权平均和。
这些性质是和我们通俗理解上的“信息”是一致的。
那么,香农就从数学上证明了,这个度量H就必须是香农给出的对数表达形式:H(X)=-Σp(x) logp(x)
香农公式
香农信息论首先在通讯领域大放异彩,之后在加密解密、压缩、自然语言识别等多个领域都体现出了巨大价值。
信息熵是香农信息论中的第一个重要概念,之后还有另一个有名的公式:香农公式。
下一回,我们再说这个著名的香农公式。