文章目录
1.代数常数/特异元素(定义)
代数常数包括幺元和零元。
要求:找出指定代数系统中的代数常数。
2.幺元/单位元(定义)
- 左幺元:如果对集合中的任意x,都有e▲x=x,则称e为左幺元;运算表中左幺元所在的行与列首元素相同;
- 右幺元:如果对集合中的任意x,都有x▲e=x,则称e为右幺元;运算表中右幺元所在的列与其行首元素相同;
- 幺元:同时满足左幺元和右幺元的元素称为幺元。运算表中幺元所对应的行和列与运算表对应的行和列相同。
要求:判断一个元素是否为幺元以及找出一个代数系统中的幺元。
相关:幺元唯一性定理(性质)
如果一个代数系统中对于某种运算同时存在左幺元和右幺元,则:
- 左右幺元相等且均等于幺元;
- 该代数系统对于此运算的幺元唯一。
3.零元(定义)
- 如果对于集合中任意x,都有e*x=e,则称e为左零元;
- 如果x*e=e,则称e为右零元;
- 同时满足左零元和右零元的元素称为零元,运算表中零元所在的行列都与该元素相同。
要求:判断一个元素是否为零元以及找出一个代数系统中的零元。
相关:零元唯一性定理(性质)
如果一个代数系统中对于某种运算同时存在左零元和右零元,则:
- 左右零元相等且均等于零元;
- 该代数系统对于此运算的零元唯一。
相关:幺元零元不相等定理(性质)
对于一个元素个数大于一的代数系统,如果该集合同时有零元和幺元,那么零元和幺元一定不相等。
4.逆元的定义
注意:逆元是一个相对于元素而非相对于集合的概念。
- 左逆元和左可逆:对于一个存在幺元e的集合,如果对于其中一个元素a,存在b▲a=e,则称b为a的左逆元,a为左可逆;
- 右逆元和右可逆:对于一个存在幺元e的集合,如果对于其中一个元素b,存在a▲b=e,则称b为a的右逆元,a为右可逆;
- 逆元的概念:如果b同时是左逆元和右逆元,则称b为a的逆元。
要求:在代数系统中找出指定元素的逆元。
相关:逆元唯一性充要条件(性质)
如果一个代数系统中存在幺元,且每一个元素都有左逆元且对应的运算可结合,那每个元素的左逆元也是右逆元,且每个元素的逆元唯一。
相关题型
题型汇总:
- 根据二元运算表指出左右幺元(左同首行,右同首列)
- 根据二元运算表指出左右零元(左同行首,右同列首)
- 找出常见代数系统的幺元和零元
1.设集合S共有四个元素,在S上定义的两个二元运算的运算表如下所示,请指出左幺元或右幺元。
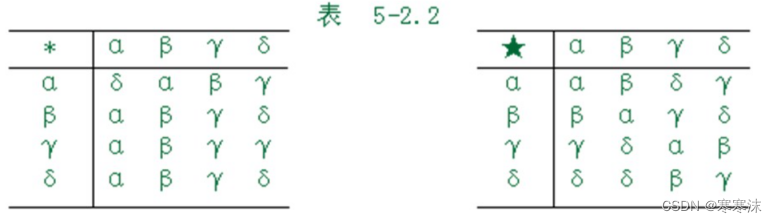
解析:本题考察根据二元运算表判定左右幺元。
在二元运算表中,左幺元所在的行的元素与其列首所在行元素相同,右幺元所在的列的元素与其行首所在列元素相同。由该结论可知对于*运算,β和sita是左幺元,没有右幺元;对于★运算,α是右幺元,没有左幺元。同时,也可以判断该代数系统中不含有幺元。
2.代数系统A=<{a,b,c},※>,用下表定义,请指出左右幺元和左右零元。
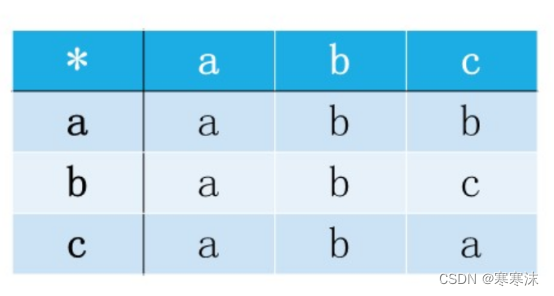
解析:本题考察根据二元运算表判定左右幺元和左右零元。
该代数系统中b为左幺元,没有右幺元;在二元运算表中,左零元所在的行元素都等于行首元素,右零元所在的列都等于列首元素,因此可以判断该代数系统中a和b是右零元,没有左零元。
3.指出代数系统<I,×>,<P(s),∩,∪>和<N,+>的幺元和零元。
解析:本题考察常用代数系统的幺元和零元。
整数乘法的幺元是1,零元是0;
幂集的交运算的幺元是全集,零元是空集,并运算的幺元是空集,幺元是全集;
自然数加法的幺元是零,没有零元。
4.证明代数系统的零元唯一性定理
解析:本题属于具有一定难度的证明题,直接从定义出发,用反证法证明。首先假设左右零元存在且不等,设左零元为el,右零元为er,则将右零元视为一般元素有el×er=el,将左零元视为一般元素有el×er=er,所以el=er,设都等于e。假设存在e’也为零元,则将e视为一般元素有e×e’=e’,将e’视为一般元素有e×e’=e,所以e=e’,矛盾。
5.考虑代数系统<R,+,>,其中R为实数集,+和分别表示普通的加法和乘法,问其中是否每一个元素都有逆元?如果有逆元,逆元是什么?
解析:本题属于理解题,考察逆元的定义。
对于加法,其幺元为0,因此每个元素都存在逆元,即自己的相反数;
对于乘法,幺元为1,除了0以外每个元素都有自己的逆元,即自己的倒数。
6.指出代数系统<N,+>的逆元,其中N是自然数集而+是指通常的加法。
解析:本题属于理解题,考察逆元的定义。
对于自然数的加法,幺元为0,但是除了0之外任何一个元素的相反数都不是自然数,因此只有元素0存在逆元为0。
7.代数系统<Z+,*>满足哪些性质?并指出其特殊元素,运算表示求两个数的最小公倍数。
解析:本题属于理解题,综合考察了二元运算性质和代数系统的特殊元素的定义。
由上一章的内容可知该代数系统满足封闭性、交换性、结合性,幂等律;求两个数最小公倍数的幺元为1,不存在零元,只有1存在逆元为其本身而其他元素都不存在逆元。
8.假设A={a,b,c},A上的三个二元运算如下图所示,判断下面三个运算是否满足交换律和幂等律,同时求出三个运算的幺元、零元和所有可逆元素的逆元。

解析:本题属于综合理解题,考察两种运算律和代数系统的特殊元素的定义。
由三个二元运算表可知*运算满足交换律,不满足幂等律,a为幺元,不存在零元,a的逆元为a,b的逆元为c,c的逆元为b;
第二个运算满足交换律和幂等律,a为幺元,b为零元,a的逆元为a;
第三个运算不满足交换性,满足幂等律,a,b,c都是左幺元,但是不存在幺元,a,b,c都是右零元,但是不存在零元,因为不存在幺元所以一定不存在逆元。
9.如下图所示:
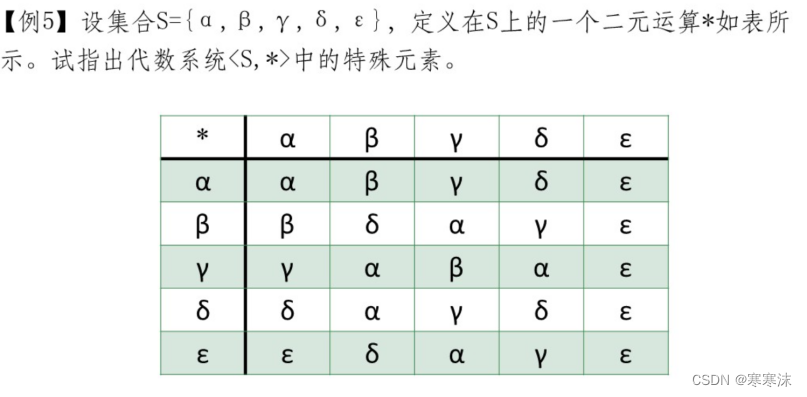
解析:本题为简单理解题,考察特殊元素的定义。
由表可知a是幺元,∈是右零元。
10.设集合S={α,β,γ,d},定义在S上的一个二元运算*如下表所示,求出该代数系统中的特殊元素。
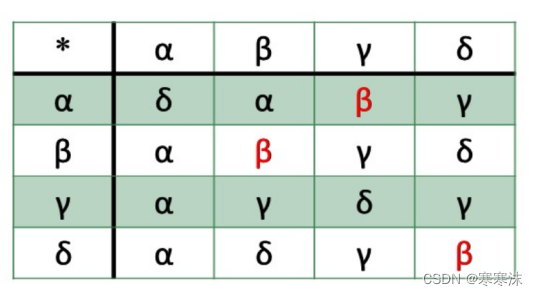
解析:该题与上题类似。由二元运算表可知β是幺元,不存在零元。
11.下列代数系统A中,哪一个没有单位元?
A.A=R,a▲b=a+b+2ab
B.A=R,a*b=|a-b|
C.A=Mn(R),运算是矩阵乘法
解析:本题为简单理解题,考察幺元的定义。
A选项中,由于该运算可交换,并且a*0=a+0=0=a,因此0是该代数系统的幺元;
B选项中不存在幺元;
C选项中幺元为n阶单位矩阵。
12.二元运算×有两个左零元,则该运算一定是()
A.不满足交换律
B.满足交换律
C.不满足结合律
D.满足结合律
解析:本题为有一定难度的理解题,考察零元的定义。
设两个左零元分别为el1和el2,则el1×el2=el1,el2×el1=el2。如果满足交换律,则有el1×el2=el2×el1=el2,说明el1=el2,即只有一个左零元,与假设矛盾,因此该运算不满足交换律。
13.下列集合和运算构成的代数系统是否满足交换律、结合律?求出该运算的幺元、零元和所有可逆元素的逆元。①有理数集合Q,x×y=(x+y)/2;②自然数集合N,x×y=2^(xy);③正整数集合Z+,x×y=gcd(x,y);④实数集合R,x×y=|x-y|;⑤整数集合Z,x×y=x+y+xy。
解析:本题为简单的综合题,综合考察交换律和结合律,以及幺元、零元和逆元的定义。
①中的运算满足交换律,但是不满足结合律,幺元不存在,零元不存在,不存在可逆元;
②中的运算满足交换律,不满足结合律,幺元不存在,零元不存在,可逆元不存在;
③中的运算满足交换律和结合律,幺元不存在,零元为1,不存在可逆元;
④中的运算满足交换律,不满足结合律,幺元不存在,零元不存在,可逆元不存在;
⑤中的运算满足交换律和结合律,幺元为0,零元为-1,可逆元计算得为-x/(1+x)=-1+1/(1+x),由于是整数,所以x取取指只能是0或-2,得到的可逆元为0或-2,0的逆元为0,-2的逆元为-2。