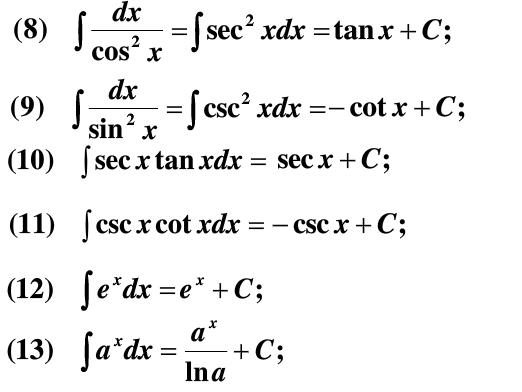1. 导数
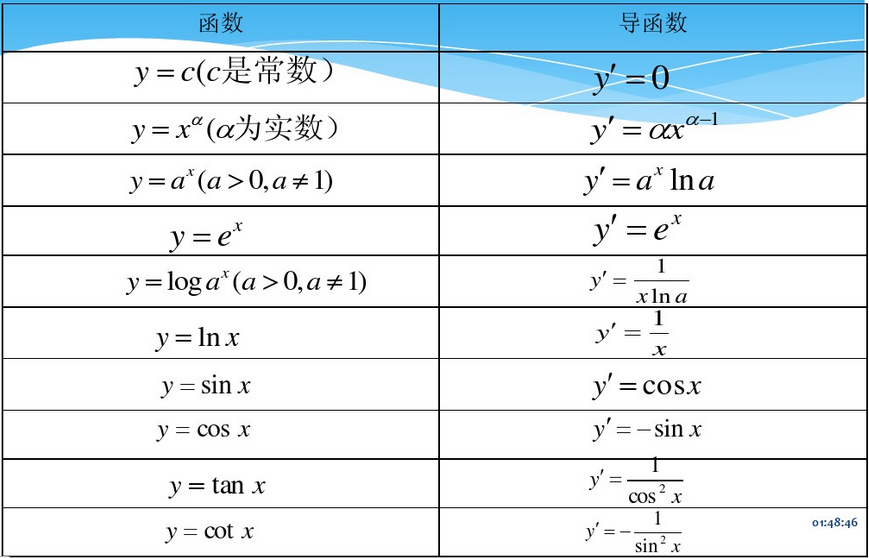
1.1 导数基本公式
1.2 导数的四则运算法则
1.3 复合函数求导法则
2. 积分
积分是微分的逆运算,即知道了函数的导函数,反求原函数。在应用上,积分作用不仅如此,它被大量应用于求和,通俗的说是求曲边三角形的面积,这巧妙的求解方法是积分特殊的性质决定的。
2.1 不定积分
设
是函数f(x)的一个原函数,我们把函数f(x)的所有原函数F(x)+C(C为任意常数)叫做函数f(x)的不定积分,记作,即∫f(x)dx=F(x)+C.其中∫叫做积分号,f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式,C叫做积分常数,求已知函数不定积分的过程叫做对这个函数进行积分。
2.2 定积分
积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说,对于一个给定的实函数f(x),在区间[a,b]上的定积分记为:
若f(x)在[a,b]上恒为正,可以将定积分理解为在Oxy坐标平面上,曲由线(x,f(x))、直线x=a、x=b以及x轴围成的面积值(一种确定的实数值)
。
。
2.3 基本积分公式
2.4 积分的基本运算法则
版权声明:本文为MyArrow原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。