隐马尔可夫模型HMM学习备忘
隐马尔可夫模型示意图如图
[1]
:

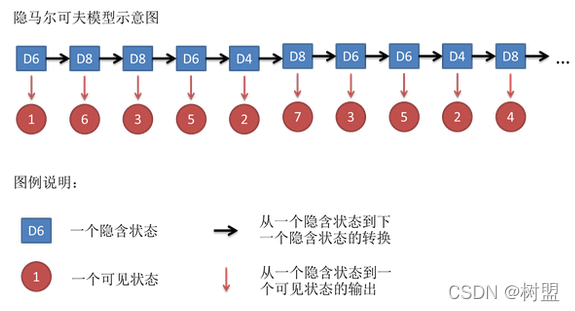
隐含状态转换关系示意图:

1、马尔可夫模型的理解
包含
N
N
N
个状态的系统,马尔可夫过程是状态
S
i
S_i
S
i
(在此
q
t
q_t
q
t
为状态
S
i
S_i
S
i
在时间
t
t
t
的状态变量)变化转移过程,状态转移依赖前
p
个状态,与其他时刻状态无关,称之为
p阶马尔可夫过程
。
系统状态间不独立时有:
p
(
q
t
=
S
i
∣
q
t
−
1
=
S
j
,
q
t
−
2
=
S
k
,
⋯
,
q
t
−
N
+
1
=
S
n
)
=
p
(
q
t
=
S
i
∣
q
t
−
1
=
S
j
,
q
t
−
2
=
S
k
,
⋯
,
q
t
−
p
+
1
=
S
n
)
,
其
中
,
p
<
N
p(q_t=S_i|q_{t-1}=S_j,q_{t-2}=S_k,\cdots,q_{t-N+1}=S_n)=p(q_t=S_i|q_{t-1}=S_j,q_{t-2}=S_k,\cdots,q_{t-p+1}=S_n),其中,p<N
p
(
q
t
=
S
i
∣
q
t
−
1
=
S
j
,
q
t
−
2
=
S
k
,
⋯
,
q
t
−
N
+
1
=
S
n
)
=
p
(
q
t
=
S
i
∣
q
t
−
1
=
S
j
,
q
t
−
2
=
S
k
,
⋯
,
q
t
−
p
+
1
=
S
n
)
,
其
中
,
p
<
N
系统状态间独立时有:
p
(
q
t
=
S
i
∣
q
t
−
1
=
S
j
,
q
t
−
2
=
S
k
,
⋯
,
q
t
−
N
+
1
=
S
n
)
=
p
(
q
t
=
S
i
)
p(q_t=S_i|q_{t-1}=S_j,q_{t-2}=S_k,\cdots,q_{t-N+1}=S_n)=p(q_t=S_i)
p
(
q
t
=
S
i
∣
q
t
−
1
=
S
j
,
q
t
−
2
=
S
k
,
⋯
,
q
t
−
N
+
1
=
S
n
)
=
p
(
q
t
=
S
i
)
2、隐马尔可夫模型
在隐马尔可夫模型(HMM)中,我们不知道模型具体的状态序列,只知道状态转移的概率,即模型的状态转换过程是不可观察的。
因此,该模型是一个双重随机过程,包括模型的状态转换和特定状态下可观察事件的随机
[2]
2.1、HHM的组成
-
状态数
NN
N
; -
每个状态可能的符号数
Mi
M_i
M
i
; -
状态转移概率矩阵
A\boldsymbol{A}
A
(要素1);
ai
j
a_{ij}
a
i
j
表示在任意时刻
tt
t
,若状态为
Si
S_i
S
i
,则下一刻状态为
Sj
S_j
S
j
的概率 -
从状态观测到状态符号集下某个符号的概率转移矩阵
B\boldsymbol{B}
B
(要素2);
bi
j
b_{ij}
b
i
j
表示任意时刻t,若状态为
Si
S_i
S
i
,则状态下某个符号(观测值
Oj
O_j
O
j
)被捕获的概率 -
模型在初始时刻,状态
Si
S_i
S
i
出现的概率,初始状态的概率分布
πi
\pi_i
π
i
(要素3)。
相较于马尔可夫模型,隐马尔可夫模型多了各个状态状态下某个符号(观测值
O
j
O_j
O
j
)的观测概率。
给定隐马尔可夫模型
λ
=
[
π
,
A
,
B
]
\lambda=[\boldsymbol{\pi},\boldsymbol{A},\boldsymbol{B}]
λ
=
[
π
,
A
,
B
]
,可按照如下过程产生观测序列
{
X
1
,
X
2
,
⋯
,
,
X
n
}
{\{X_1,X_2,\cdots,,X_n\}}
{
X
1
,
X
2
,
⋯
,
,
X
n
}
step1:设置
t
=
1
t=1
t
=
1
,并根据初始状态概率
π
\boldsymbol{\pi}
π
选择初始状态
Y
1
Y_1
Y
1
;
step2:根据状态值
Y
t
Y_t
Y
t
(
S
i
S_i
S
i
)和输出观测概率
B
\boldsymbol{B}
B
选择观测变量取值
X
t
X_t
X
t
(在特定状态符号集合内);
step3:根据观测变量取值
Y
t
Y_t
Y
t
和状态转移矩阵
A
A
A
转移模型状态,即确定
Y
t
+
1
Y_{t+1}
Y
t
+
1
2.2、HMM解决的三个基本问题
(1)
评估
:求解不同时刻对应不同状态(隐含状态
Y
t
Y_t
Y
t
)的观测序列(可见状态
X
t
X_t
X
t
)的概率;(例如:给定一个天气的隐马尔可夫模型,包括第一天的天气概率分布,天气转移概率矩阵,特定天气下树叶的湿度概率分布。求第一天湿度为 1,第二天湿度为 2,第三天湿度为 3 的概率。)
-
思路一:找到所有状态序列,得到各状态概率,得到每种状态概率对应的观察概率,求和。(找到每一个可能的隐藏状态
Yt
Y_t
Y
t
,并且将这些隐藏状态下的观察序列概率相加。) -
思路二:采用动态规划
[2]
(2)
解码
:已知不同时刻对应不同状态下观测序列(可见状态
X
t
X_t
X
t
)的概率分布,求解不同时刻对应状态情况(隐含状态
Y
t
Y_t
Y
t
);(例如:给定一个天气的隐马尔可夫模型,包括第一天的天气概率分布,天气转移概率矩阵,特定天气下树叶的湿度概率分布。并且已知第一天湿度为 1,第二天湿度为 2,第三天湿度为 3。求得这三天的天气情况。)
- 发现“最优”状态序列能够“最好地解释”观察序列
- 每一个状态单独最优不一定使整体的状态序列最优,两个最优的状态之间的转移概率可能为 0
- 采用Viterbi 搜索算法
(3)
学习
:观测序列
{
X
1
,
X
2
,
⋯
,
,
X
n
}
{\{X_1,X_2,\cdots,,X_n\}}
{
X
1
,
X
2
,
⋯
,
,
X
n
}
求解HHM模型参数
A
,
B
\boldsymbol{A},\boldsymbol{B}
A
,
B
; (例如:已知第一天湿度为 1,第二天湿度为 2,第三天湿度为 3。求得一个天气的隐马尔可夫模型,包括第一天的天气,天气转移概率矩阵,特定天气下树叶的湿度概率分布。)此过程也称之为学习。
- 给定一个观察序列,得到一个隐马尔可夫模型
-
如果产生观察序列 O 的状态已知(即存在大量标注的样本), 可以用最大似然估计来计算
μ\mu
μ
的参数,Baum-Welch 算法(前向后向算法)描述, - 如果不存在大量标注的样本:期望值最大化算法(Expectation-Maximization, EM)
一个HMM的参考实例见
[3]
参考:
[1]
一文搞懂HMM(隐马尔可夫模型]
[2]
隐马尔可夫模型(HMM)详解
[3]
HMM隐马尔可夫模型详解
[4]
隐马尔科夫模型HMM(一)HMM模型