参考书目:
- 工程电磁场导论(马西奎)
- 电磁场与电磁波(邹澎)<郑大课程选定教材>
- 知乎电磁场专栏
- 电磁场理论基础(王蔷)
整理备忘作为复习之用。本篇中所有积分符号全部采用单符号,面积和体积不再使用多积分号以便表述简单,同时符号标记使用马西奎教授的设定,在γ等地方可能和别的有所不同。
同时建议自己推导公式之后对公式有影响后再来看,因为很多地方都是用语言一笔带过公式,如果对公式不熟悉可能会看的很晕
,打公式真的好累…
鄙人学疏才浅,如有错误望多多指正
更好记的参考系及其算子
相比较《电磁场与电磁波(邹澎)》中的旋度公式,《工程电磁场导论(马西奎)》中将所有系数提到最前面的方式显然方便记忆(下图仅为圆柱坐标系,对于球坐标系同理)

静电场和恒定磁场的关系(思维导图)
这两章的引出思路,公式关系是用思维导图的方式记录的。个人感觉这两张是整本书的思想核心,其中的推导方式、公式演化在后面章节中贯穿。例如将介质扩展为无限大介质从而消除未知项、帽子算法等。
如下图:(里面的公式大家自己填吧~太懒了)

从恒定电磁场引出时变电磁场
其实更准确的说时变电磁场是由于磁场的变化从而在磁场中引入了电场的相关概念,但是又由于磁场量始终在变所以磁场和电场同时是随时间在变的。
先引入
电磁场与电磁波(邹澎)<郑大课程选定教材>
中没有提到的保守场问题
-
保守场的旋度为零,静电场是静止电荷激发的,作为保守场无旋有源,所以
∮l
E
⃗
d
l
=
e
i
=
0
\oint_{l}{\vec{E}dl=ei=0}
∮
l
E
d
l
=
e
i
=
0
-
非保守场的旋度不为零,感生电场是磁场激发的,作为非保守场(有源场)无旋有源,所以
∮l
E
⃗
d
l
=
e
i
≠
0
\oint_{l}{\vec{E}dl=ei\neq0}
∮
l
E
d
l
=
e
i
=
0
于是我们开始从电磁场引出时变电磁场
1.
关于环路定理的变换
首先明确环路定理可以从能量做功的角度(位置功只与位置相关)推导出来(
W
=
q
∫
l
E
⃗
d
l
W=q\int_{l}\vec{E}dl
W
=
q
∫
l
E
d
l
)
所以在静电场中的基本方程之一:电场闭合环路积分为零 在这里不再适用。引出了时变电场的环路定理:
∮
l
E
⃗
d
l
=
e
i
≠
0
\oint_{l}{\vec{E}dl=ei\neq0}
∮
l
E
d
l
=
e
i
=
0
2.
关于随时间而变化的电场
E
=
E
库
+
E
i
E=E_库+E_i
E
=
E
库
+
E
i
所以当对两边积分的时候,库仑电场的积分为零,感应电场的积分由感生电动势和动生电动势共同组成(这里注意分开计算的时候其中的感生电动势是不考虑面积变化的,当你考虑了面积变化就相当于通过变化磁通微分来直接计算)
通过两边积分后引用面积分线积分之间的转换,可以得到(注意下面公司中向量将省去箭头)
∇
×
E
⃗
=
−
∂
B
∂
t
+
∇
×
(
∇
v
×
B
)
\nabla\times\vec{E}=-\frac{\partial B}{\partial t}+\nabla\times(∇v×B)
∇
×
E
=
−
∂
t
∂
B
+
∇
×
(
∇
v
×
B
)
其中
∇
×
(
∇
v
×
B
)
\nabla\times(∇v×B)
∇
×
(
∇
v
×
B
)
在我们讨论时变磁场是默认为零不在讨论。
3.
电流密度的变化
电流密度不再由单一,将有静电场中的电流密度概念和传导电流密度概念共同组成。这也直接影响了磁场强度的旋度的结果变化,多了传导电流一项。
其中传导电流密度为对于电位移的时间微分。推导方式既可以通过书上的电流连续性定理推导,也可以通过非闭合面积分任意变化(引自马西奎教学视频的思想)来推导。
4.
由上面的内容我们可以进一步得到麦克斯韦方程
说简单点麦克斯韦方程就是把电场和磁场的方程全部放了进来
同时也由于麦克斯韦方程组,过去我们求边界条件的方式中一些公式发生了改变。但是由于极限的思想,整体的边界条件并无变化,只是边界条件由静电场边界条件和恒定磁场边界条件共同组成(双倍快乐)
5.
能量的变化
能量也变成了组合~
6.
动态位
静电场中我们引入了电位,恒定电场中我们引入了磁矢量位和标量位,利用同样的方法可以得到时变磁场中的矢量位和标量位。两者共同组成了动态位(注意这是后面推导达拉贝尔和坡印廷矢量方程的关键)公式很好推导,需要引入一个常用公式:
∇
×
∇
×
A
=
∇
(
∇
∙
A
)
−
∇
2
A
\nabla\times\nabla\times A= \nabla(\nabla\bullet A)-\nabla^2 A
∇
×
∇
×
A
=
∇
(
∇
∙
A
)
−
∇
2
A
7.
达朗贝尔方程和坡印廷矢量
为什么把这两个放在一起呢?因为其实两个的推导核心是一样的。都是利用动态位带入麦克斯韦方程组来回变换得到。具体推导不再详述,注意达朗贝尔方程存在附加条件以便简便运算和唯一。详细的求解会在后面章节叙述
平面电磁波
引一
我们需要先清楚理想介质、导电媒质、理想导体的关系。
- 无源理想介质的J=0,ρ=0,电导率为零(不导电)
- 导电媒质又叫做损耗媒质,可以分为良和弱。良导电媒质的电导率很大,弱导电媒质的电导率很小。
- 理想导体电导率看做无穷大,同时理想导体E=0
这样一来你可以理解为导电媒质是理想导体和理想介质的掺杂体,虽然有失严谨但是在后面中这种理解帮助很大
引二
我们可以引入复数形式来方便计算。复数形式中微分和积分将会简化为普通乘法计算,对于整理极为方便。详细推导个人感觉邹澎书的推导过程更易接受。但是其中有一些没有铺垫的部分,下面也会提到。
整个复数形式的核心:①
E
⃗
(
x
,
y
,
z
,
t
)
=
E
⃗
˙
(
x
,
y
,
z
)
e
j
ω
t
\vec{E}(x,y,z,t)=\dot{\vec{E}}(x,y,z)e^{jωt}
E
(
x
,
y
,
z
,
t
)
=
E
˙
(
x
,
y
,
z
)
e
j
ω
t
②
E
⃗
˙
(
x
,
y
,
z
)
=
E
m
e
˙
i
φ
=
E
m
⋅
e
⃗
⋅
e
i
φ
\dot{\vec{E}}(x,y,z)=\dot{E_me}^{i\varphi}=E_m·\vec{e}·e^{i\varphi}
E
˙
(
x
,
y
,
z
)
=
E
m
e
˙
i
φ
=
E
m
⋅
e
⋅
e
i
φ
(后面的
E
x
1
˙
=
E
m
1
+
˙
e
−
γ
z
+
E
m
1
−
˙
e
γ
z
\dot{E_{x1}}=\dot{E_{m1}^+}e^{-\gamma z}+\dot{E_{m1}^-}e^{\gamma z}
E
x
1
˙
=
E
m
1
+
˙
e
−
γ
z
+
E
m
1
−
˙
e
γ
z
只是根据波动方程得到的关于解的形式,切记和这里的e是没有关系的)
引三
从而引出复数形式的麦克斯韦方程组
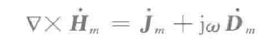
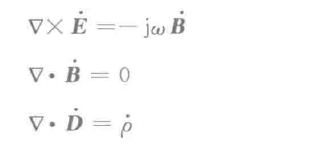
为什么要把第一个式子单独截出来呢?因为这个是后面讨论的重点。
我们先从简单地出发,如果是在理想介质中
,Jm便是零,从而第一个式子右端只剩下D项。于是我们可以通过对第二个式子两端同时求旋度,并继续使用我们在时变电场中提到的
∇
×
∇
×
A
=
∇
(
∇
∙
A
)
−
∇
2
A
\nabla\times\nabla\times A= \nabla(\nabla\bullet A)-\nabla^2 A
∇
×
∇
×
A
=
∇
(
∇
∙
A
)
−
∇
2
A
来化简,得到在理想介质中的波动方程:
-
①
∇2
E
⃗
−
1
v
2
∂
2
E
⃗
∂
t
2
=
0
\nabla^2\vec{E}-\frac{1}{v^2}\frac{\partial^2\vec{E}}{\partial t^2}=0
∇
2
E
−
v
2
1
∂
t
2
∂
2
E
=
0
-
②
∇2
H
⃗
−
1
v
2
∂
2
H
⃗
∂
t
2
=
0
\nabla^2\vec{H}-\frac{1}{v^2}\frac{\partial^2\vec{H}}{\partial t^2}=0
∇
2
H
−
v
2
1
∂
t
2
∂
2
H
=
0
我们发现其中有两个未知量,EH。E和H有什么关系?暂时有两个我们需要记住的关系,一是他们的叉乘等于玻印亭矢量,同时波印廷矢量平均值的复数形式表示为
S
a
v
=
1
2
R
e
[
E
˙
×
H
˙
∗
]
S_{av}=\frac{1}{2}Re[\dot{E}\times{\dot{H}}^*]
S
a
v
=
2
1
R
e
[
E
˙
×
H
˙
∗
]
(1/2可以这样简单理解:cos函数的平均值是多少?初中就知道是1/2。不严谨但是好记)。二是麦克斯韦方程组的第二个公式。在后面的推导中第二个公式起到了连接E和H的关键作用。
于是我们尝试解E和H。引入复数来简化,同时我们假定这个波是沿着z方向运动的平面电磁波。通过简单的计算我们可以得到一个同一形式:
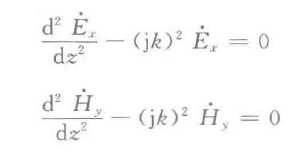
这里注意,不同的教材上面设定的k不太一样。这里是设定
k
=
w
μ
ε
k=w\sqrt{\mu\varepsilon}
k
=
w
μ
ε
,有一些是设定
k
=
j
w
μ
ε
k=jw\sqrt{\mu\varepsilon}
k
=
j
w
μ
ε
,无伤大雅。其目的最终都是化简。配合微积分知识以及傅里叶变换可以得到瞬时形式:
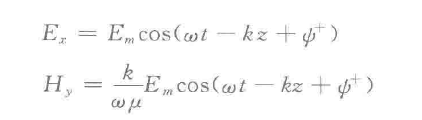
同时我们把两者的比值称为波阻抗。由于波阻抗是个常数,我们需要思考,随着时间t和x变化的E和H怎样才能比值为常数呢?使得两者和x和t都无关即可,也就是wt-kz等于零。于是我们知道了
v
=
w
k
v=\frac{w}{k}
v
=
k
w
。记住这个公式我们在后面损失媒质中还会使用。
接下来我们讨论损失媒质
损失媒质中电导率γ不再是零,所以波动方程不再是简单地两项而是三项。
-
①
∇2
E
⃗
−
μ
ε
∂
2
E
⃗
∂
t
2
−
μ
γ
∂
E
⃗
∂
t
=
0
\nabla^2\vec{E}-\mu\varepsilon\frac{\partial^2\vec{E}}{\partial t^2}-\mu\gamma\frac{\partial\vec{E}}{\partial t}=0
∇
2
E
−
μ
ε
∂
t
2
∂
2
E
−
μ
γ
∂
t
∂
E
=
0
-
②
∇2
H
⃗
−
μ
ε
∂
2
H
⃗
∂
t
2
−
μ
γ
∂
H
⃗
∂
t
=
0
\nabla^2\vec{H}-\mu\varepsilon\frac{\partial^2\vec{H}}{\partial t^2}-\mu\gamma\frac{\partial\vec{H}}{\partial t}=0
∇
2
H
−
μ
ε
∂
t
2
∂
2
H
−
μ
γ
∂
t
∂
H
=
0
为了和理想介质中统一,我们设定了新的变量(下图符号有所不同)
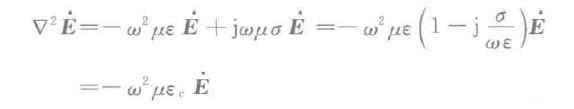
我们可以设定新的
k
′
=
w
μ
ε
c
k’=w\sqrt{\mu\varepsilon_c}
k
′
=
w
μ
ε
c
,至此上面的便和上面的形式相统一了。但是注意这里的k’是一个全复数,有实部和虚部共同组成,即k=α+jβ,我们也可以得到下面的式子(其中附加相位可有可无,不影响整体):
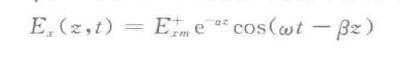
引用我们刚才的思想,如果让波阻抗等于常数,就让
v
=
w
β
v=\frac{w}{β}
v
=
β
w
。其中α和β如下:
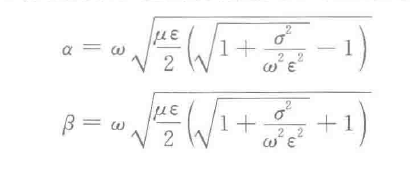
那么我们开始考虑,其中的
γ
2
w
2
ε
2
\frac{\gamma^2}{w^2\varepsilon^2}
w
2
ε
2
γ
2
对于值的影响。在导电媒质中,强导电媒质γ很大,
γ
2
w
2
ε
2
≫
1
\frac{\gamma^2}{w^2\varepsilon^2}\gg1
w
2
ε
2
γ
2
≫
1
,所以可以得到
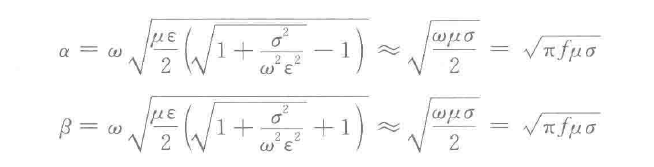
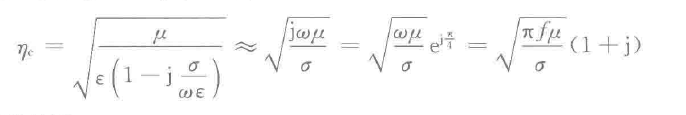
同理可以得到弱导电媒质:

这些公式个人感觉最好的方式是自己推导而不是强行记住,只需要知道怎么来的其实一切都很简单。
但是这些的作用是什么呢?
正文
我们来开始讨论入射折射问题。我们先讨论两种媒质分界面的垂直入射。请注意这里我们讨论的是媒质但是并没有说明是导电媒质。
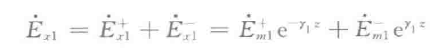
说明:这里的γ对应的k’
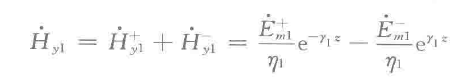
这里边用到了上面说介绍的部分。对于理想导体,由于无电场,全反射。而对于理想介质,相当于k中不存在衰减项实数,只存在有虚数部分。由此可以很轻松的引出理想介质的对应方程,并且写出理想介质的合场强瞬时形式(左边为矢量,对照前面的引入就可以推出)
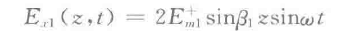
同时引入趋肤深度δ,并且对波阻抗进行进一步分析。当分析导电媒质的时候,k不再是理想导体中的简单表达式,而是由
ε
\varepsilon
ε
复合形式存在。于是波阻抗变成了一个由实部虚部组成的复数形式。其中的实部对应表面电阻,虚部对应表面电抗。这里顺便提一下,波阻抗所描述的并不是能量的损耗,而是电场磁场的相互转换过程。